Understanding The Normal Curve And Z-Scores: A Guide To Probability

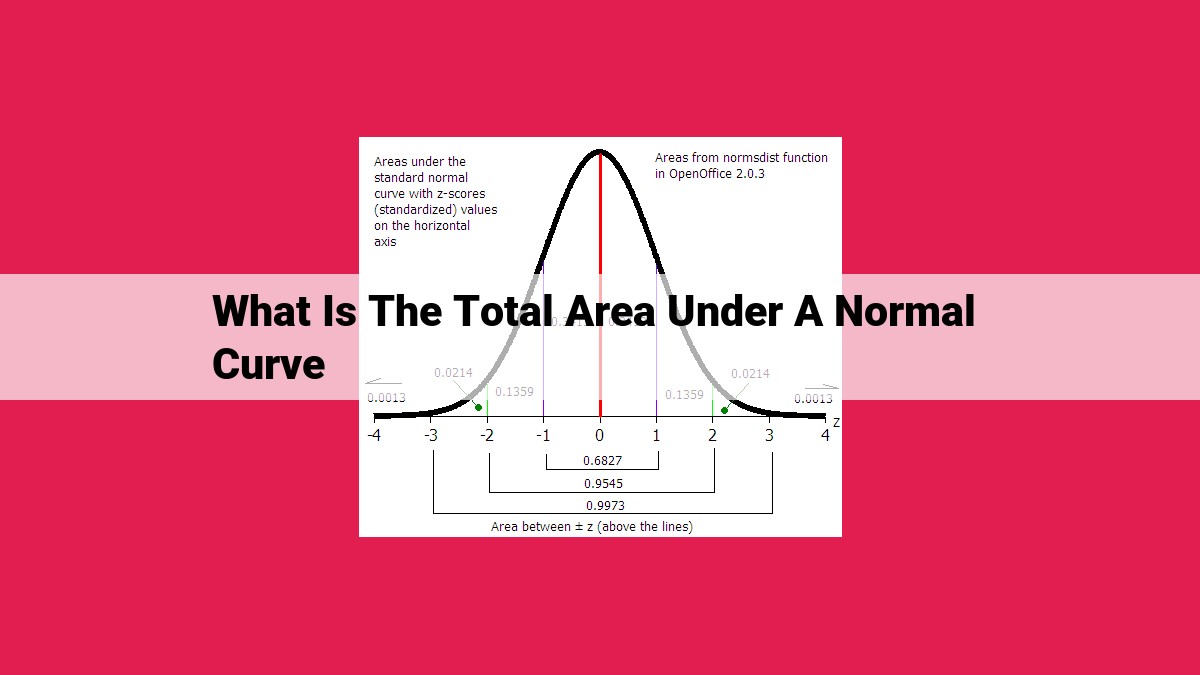
The total area under a normal curve is always 1, representing the probability of any outcome. The normal distribution, also known as the bell curve, is a symmetrical distribution characterized by its mean and standard deviation. The standard normal distribution (z-distribution) is a standardized version of the normal distribution with a mean of 0 and a standard deviation of 1. Z-scores can be used to find the area under any normal curve by converting any value to a corresponding z-score. The formula for calculating the area under a normal curve between two z-scores involves the use of the standard normal distribution function. This concept is essential in statistics and probability, as it allows for the calculation of probabilities and making statistical inferences.

Unlocking the Secrets of the Normal Curve: The Bell Curve of Statistical Insights

The normal curve, affectionately known as the bell curve or Gaussian distribution, is the backbone of statistics and probability. It serves as a powerful tool for analyzing data, predicting outcomes, and making informed decisions. Picture a symmetrical, bell-shaped curve that encapsulates the distribution of countless variables in the real world, from heights and weights to test scores and financial returns.

Understanding the Essence of the Normal Curve

At the heart of the normal curve lies the Central Limit Theorem, a statistical marvel that asserts that as sample size increases, the distribution of sample means approaches a normal distribution, irrespective of the underlying distribution of the original data. This remarkable property makes the normal curve a universal tool for modeling and analyzing data from diverse sources.

The normal distribution is defined by two key parameters: the mean (μ), which represents the average value of the data, and the standard deviation (σ), which measures the spread or dispersion of the data. The mean determines the center of the curve, while the standard deviation governs the width and height of the bell.

Understanding the Normal Distribution

The normal distribution, also known as the bell curve or Gaussian distribution, is a cornerstone of statistics. Its ubiquity stems from its ability to model diverse phenomena, from test scores to stock market fluctuations.

Central to the normal distribution is the Central Limit Theorem. This theorem states that the average of a large number of independent random variables tends to follow a normal distribution, regardless of the underlying distribution of the individual variables. This remarkable property makes the normal distribution an indispensable tool for making statistical inferences from sample data.

In defining a normal distribution, two parameters play a crucial role: the mean (μ) and standard deviation (σ). The mean represents the center of the distribution, while the standard deviation measures the spread of data around the mean. A smaller standard deviation indicates that data is clustered closer to the mean, while a larger standard deviation signifies greater dispersion.

These parameters shape the bell-shaped curve of the normal distribution. The curve is symmetric around the mean, with the frequency of data points decreasing gradually as we move away from the center. The area under the curve represents the probability of a particular value occurring. Understanding the normal distribution is essential for comprehending a wide range of statistical concepts, from hypothesis testing to confidence intervals.

Understanding the Total Area Under the Normal Curve

The normal distribution, also known as the bell curve, is an essential concept in statistics that describes the distribution of randomly collected data. It’s characterized by its distinctive shape, resembling a symmetrical bell, with most data points clustering around the mean and fewer data points at the extremes.

The total area under the normal curve is always 1, no matter what the mean and standard deviation are. This fundamental property makes it possible to calculate the probability of an event occurring within any given range of values.

The Standard Normal Distribution (z-Distribution)

The standard normal distribution is a special case of the normal distribution that has a mean of 0 and a standard deviation of 1. It is represented by the z-score, which converts any value from a normal distribution to a corresponding value in the standard normal distribution.

Calculating the z-score involves subtracting the mean from the value and dividing the result by the standard deviation.

z = (x - μ) / σ

where x is the original value, μ is the mean, and σ is the standard deviation.

Standard Normal Distribution: A Closer Look

In the realm of probability and statistics, the standard normal distribution plays a pivotal role. It’s a bell-shaped curve that emerges from the bell curve, also known as the normal distribution, when we standardize the data. This standardization process transforms data into a standard format, allowing for comparisons across different distributions.

Meaning of Z-Scores

The key to understanding the standard normal distribution lies in z-scores. A z-score measures how many standard deviations a data point is away from the mean. For example, a z-score of 1 indicates that the data point is one standard deviation above the mean. Conversely, a z-score of -2 implies that the data point is two standard deviations below the mean.

Calculation of Z-Scores

Calculating z-scores is straightforward. Simply subtract the mean from the data point and divide the result by the standard deviation:

z-score = (data point - mean) / standard deviation

Properties and Characteristics

The standard normal distribution possesses several key properties:

• Symmetrical: The curve is symmetrical around the mean, which is always zero.
• Bell-shaped: It has a bell-shaped curve, with most data points clustering around the mean.
• Total area equals 1: The total area under the curve is always 1, representing the entire population.
• Fixed standard deviation: The standard deviation is always 1, indicating that the curve is spread out by the same amount.

These properties make the standard normal distribution a useful tool for making inferences about a population when only a sample is available. By standardizing the data, we can compare different distributions and make probabilistic statements about the population.

Finding the Total Area Under a Normal Curve

In the realm of statistics and probability, the normal curve, also known as the bell curve or Gaussian distribution, is a fundamental concept that reveals the natural patterns of data distribution. It resembles the familiar bell-shaped curve, smoothly sloping from a central peak and gradually trailing off towards the tails.

The normal distribution is defined by two crucial parameters: the mean and the standard deviation. The mean represents the average value of the data, while the standard deviation measures how spread out the data is from the mean.

To determine the total area under the normal curve between any two given z-scores, we utilize the standard normal distribution, a variation of the normal distribution with a mean of 0 and a standard deviation of 1.

Steps for Calculating the Total Area:

1. Convert the two given data points into z-scores using the formula:

z = (x - μ) / σ

where:
* x is the data point
* μ is the mean
* σ is the standard deviation

2. Locate the area corresponding to each z-score using the standard normal distribution table or a statistical calculator.

3. Subtract the area corresponding to the smaller z-score from the area corresponding to the larger z-score to obtain the total area between the two z-scores.

Formula:

Area = Φ(z2) - Φ(z1)

where:
* Φ is the cumulative distribution function of the standard normal distribution
* z1 is the smaller z-score
* z2 is the larger z-score

This formula provides a powerful tool for determining the probability of a data point falling within a specific range of values. It forms the foundation for a vast array of statistical applications, from hypothesis testing to confidence interval estimation.

Related Concepts in Statistics and Probability

Navigating the realm of statistics and probability can be daunting at first, but like exploring a new world, understanding the key concepts is the compass that guides you. Enter the normal curve, the bell-shaped beauty that underpins many statistical analyses.

As we delve deeper, we encounter the Central Limit Theorem, the enigmatic force that transforms the bumpy road of individual data points into the smooth curve of the normal distribution. The mean, the heart of the curve, and the standard deviation, its breadth, dance together to define the unique shape of each normal curve.

Now, let’s shift our gaze to the area under the curve. Just as the entire ocean holds all its water, the total area beneath the normal curve is always one. And just as we can divide the ocean into regions, we can use z-scores to partition the normal curve, unlocking its secrets.

Z-scores are simply a way to measure how far a data point lies from the mean in terms of standard deviations. This allows us to compare data from different normal distributions on a common scale.

With the power of z-scores, we can calculate the area under any normal curve between two points, uncovering the probability of observing a data point within that range. Armed with this knowledge, we can make statistical inferences, test hypotheses, and draw meaningful conclusions from our data.

The concepts of integration, census, sampling, demography, bias, sampling error, confidence interval, median, mode, range, variance, standard error, hypothesis testing, and confidence levels all play vital roles in the statistical tapestry, each contributing a unique thread to the grand design.

So, dear reader, as you embark on your statistical adventures, remember the normal curve, its related concepts, and the story they tell. They are the keys that unlock the treasure trove of knowledge hidden within your data.