Uncovering The Mysteries Of Nonlinear System Solutions: A Phase Portrait

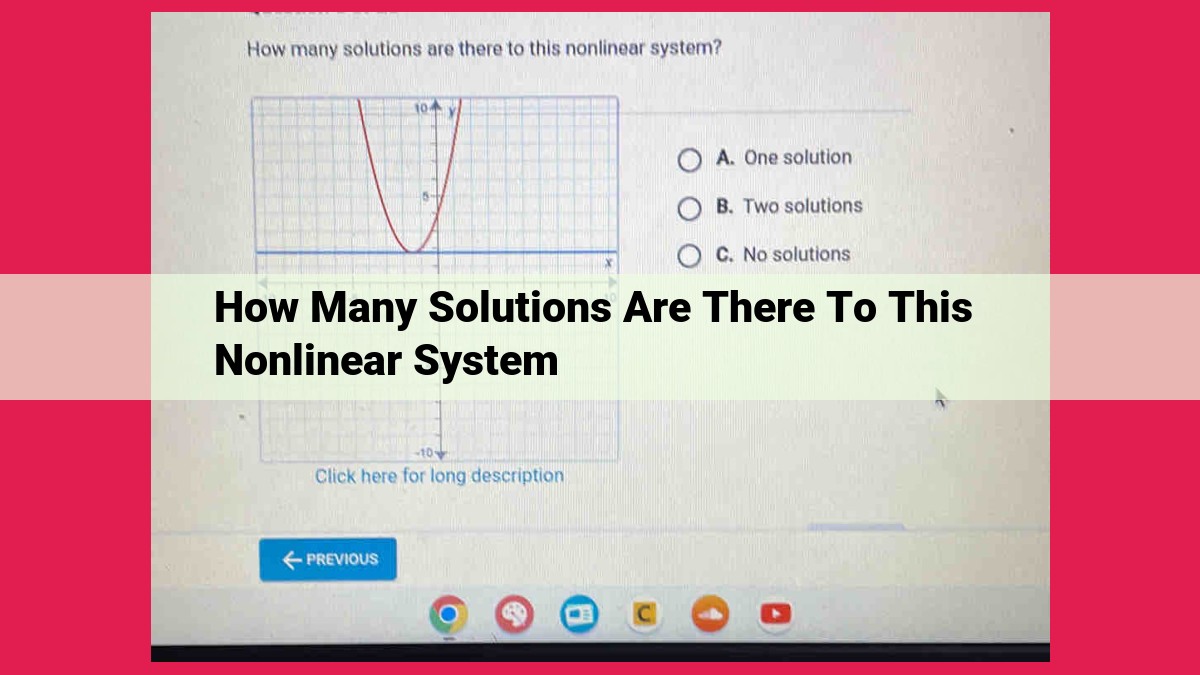
The number of solutions to a nonlinear system of equations depends on the properties of the system. The system may have one, multiple, or infinitely many solutions. The specific number of solutions can be determined by examining the system’s phase portrait, which provides a graphical representation of system trajectories. By identifying critical points, trajectories, and basins of attraction, the phase portrait can reveal the existence and behavior of possible solutions to the nonlinear system.

Understanding the Flow of Nonlinear Systems: Isoclines and Related Concepts

In the realm of nonlinear systems, isoclines play a crucial role in unraveling the intricate dance of trajectories. Isoclines are curves in the phase plane where a particular component of the system’s derivative is zero. This implies that trajectories along an isocline flow in a parallel manner.

Visualizing the slope field of a system helps us understand the direction of its trajectories. At any given point in the phase plane, the slope field indicates the direction in which the system tends to move. Regions where isoclines intersect create nullclines, where trajectories tend to parallel the respective axes.

Flow lines are paths traced out by solutions to the system’s differential equations. Isoclines provide a graphical representation of the direction and flow of trajectories, helping us piece together a comprehensive picture of the system’s dynamics.

In summary, isoclines, slope fields, nullclines, and flow lines are interconnected concepts that collectively paint a vivid picture of the flow of nonlinear systems, enabling us to predict their behavior and gain insights into their underlying dynamics.

Phase Portrait: Unveiling the Dynamics of Nonlinear Systems

When navigating the intricate world of nonlinear systems, a phase portrait emerges as an indispensable tool. It’s a graphical representation that vividly portrays the flow of trajectories within the system, providing invaluable insights into its dynamics.

Trajectories: Mapping the Dance of Time

Trajectories, the paths traced by the system’s state over time, are at the heart of a phase portrait. These curves depict the evolution of the system, showcasing how it responds to initial conditions and system parameters.

Critical Points: Resting or Restless?

Critical points, also known as equilibrium points, represent states where the system’s rate of change is zero. These points are like crossroads, where trajectories may converge or diverge, indicating stability or instability, respectively.

Basins of Attraction: Guiding the System’s Fate

Basins of attraction are regions in the phase portrait where trajectories inevitably converge towards a critical point. These basins represent the attractors of the system, shaping its ultimate trajectory and informing our understanding of its long-term behavior.

Unveiling Nonlinear Dynamics: A Visual Exploration

Phase portraits, with their intricate web of trajectories, provide a visual tapestry that unveils the complexities of nonlinear systems. They enable us to identify critical points, determine stability, explore bifurcations, and delve into the intricate dance of these systems over time. By harnessing the power of a phase portrait, we gain a deeper understanding of the fascinating world of nonlinear dynamics.

Equilibrium Points

• Define equilibrium points and describe their importance in analyzing system dynamics.
• Explain different types of equilibrium points, such as fixed points, critical points, and stationary points.

Equilibrium Points: Navigating the Dynamics of Nonlinear Systems

In the intricate dance of nonlinear systems, equilibrium points emerge as pivotal players, shaping the overall dynamics and behavior of these fascinating systems. These points, where the forces acting on the system balance each other, offer crucial insights into the long-term evolution and stability of the system.

Definition and Significance

An equilibrium point, often referred to as a fixed point or critical point, is a state at which the rate of change of the system’s variables is zero. It represents a steady state, where the system is in a stable, unchanging condition.

Understanding equilibrium points is paramount in analyzing the dynamics of nonlinear systems because they provide a reference point for predicting the system’s behavior. By identifying and characterizing these points, we can gain insights into the system’s stability, its potential for oscillation, and its overall response to perturbations.

Types of Equilibrium Points

Nonlinear systems can exhibit various types of equilibrium points, each with its unique implications for system behavior:

• Stable equilibrium point: A point at which the system returns to its equilibrium state after a small disturbance.
• Unstable equilibrium point: A point from which the system departs after a small disturbance.
• Saddle point: A point at which the system’s trajectories are attracted in one direction and repelled in the perpendicular direction.
• Center: A point around which the system’s trajectories orbit.

Identifying Equilibrium Points

To identify equilibrium points in a nonlinear system, one often uses graphical techniques such as phase portraits. These portraits map out the trajectories of the system’s variables, revealing the location of equilibrium points as the points where the trajectories intersect.

Alternatively, equilibrium points can be found mathematically by solving the system’s governing equations for the values of the variables at which the rate of change is zero.

By understanding the types and properties of equilibrium points, we can unlock a deeper comprehension of nonlinear systems, enabling us to predict their behavior and design control strategies to maintain desired system states.

Stability

A crucial concept in nonlinear systems analysis, stability, assesses how trajectories behave near equilibrium points. It quantifies the system’s tendency to return to or diverge from these points.

Asymptotic Stability

Asymptotically stable equilibrium points are like magnets that attract nearby trajectories. No matter how close they start, these trajectories eventually converge to the equilibrium point. This behavior implies that the system returns to a stable state after disturbances.

Lyapunov Stability

Lyapunov stability provides a powerful mathematical framework for analyzing stability. It involves finding a function that decreases along trajectories. The rate of decrease determines the stability of the equilibrium point. A Lyapunov function can prove stability without explicitly solving the system’s equations.

Structural Stability

Structural stability considers how the system’s behavior changes under parameter variations. A structurally stable system retains its equilibrium points and stability characteristics over a range of parameters. This robustness makes structural stability essential for real-world systems where parameters can fluctuate.

By understanding stability in nonlinear systems, scientists and engineers can predict system dynamics, design control strategies, and ensure the safety and reliability of complex systems.

Bifurcation Analysis: Unveiling the Dynamics of Nonlinear Systems

Introduction
In the realm of complex systems, bifurcations emerge as intriguing phenomena that unlock a deeper understanding of how systems behave under varying conditions. Bifurcation analysis, a powerful tool in nonlinear dynamics, empowers us to decipher the intricacies of these systems as they undergo fundamental changes.

Defining Bifurcation
At its core, bifurcation refers to a qualitative change in the behavior of a system that occurs when a parameter crosses a specific threshold value. It’s like a switch being flipped, altering the system’s dynamics dramatically.

Types of Bifurcations
Bifurcations are broadly classified into two main categories:

• Local Bifurcations: These occur when the stability of a single equilibrium point changes. They involve the emergence or disappearance of equilibrium points and the alteration of their stability properties.

• Global Bifurcations: These involve more extensive changes, such as the creation or destruction of closed orbits (known as limit cycles) or the merging or splitting of equilibrium points.

Impact of Bifurcations
Bifurcations have a profound impact on the overall phase portrait of a system. They can:

• Induce New Equilibrium Points: Some bifurcations give rise to the appearance of new equilibrium points, expanding the system’s repertoire of possible behaviors.

• Alter Stability: Bifurcations can destabilize existing equilibrium points or stabilize previously unstable ones, influencing the flow of trajectories within the phase portrait.

• Create or Destroy Limit Cycles: The emergence or disappearance of limit cycles, which represent periodic oscillations, can drastically alter the system’s dynamics.

Investigating Bifurcations
Researchers employ bifurcation analysis to gain insights into the behavior of nonlinear systems. By varying a specific parameter and observing the changes in the system’s phase portrait, they can identify and characterize bifurcation points. This process helps unravel the complex dynamics that govern these systems and predict their behavior under different conditions.

Conclusion
Bifurcation analysis serves as a powerful tool for understanding the intricate dynamics of nonlinear systems. By uncovering the mechanisms that drive qualitative changes in system behavior, it empowers researchers and practitioners to better comprehend and predict the behavior of complex systems in various scientific and engineering fields.