Newton’s Second Law: Unraveling The Interplay Between Force And Acceleration
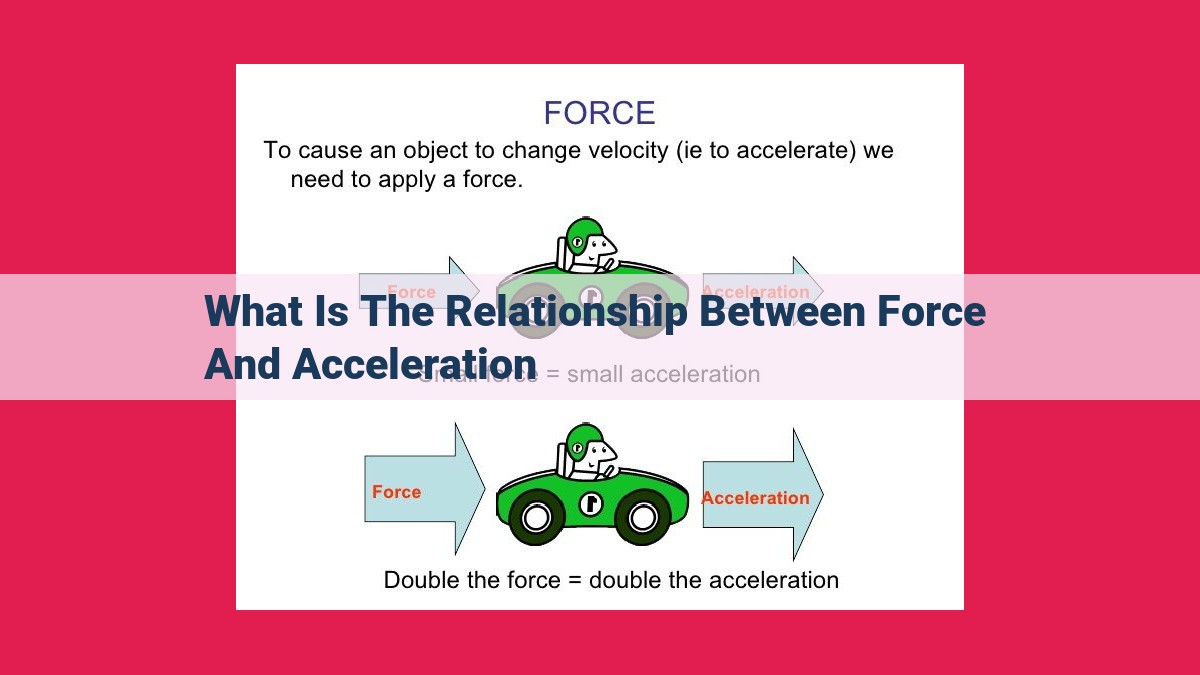
Force, a push or pull, and acceleration, the rate of change in velocity, are fundamentally intertwined. Newton’s second law of motion mathematically quantifies this relationship as F = ma, where force (F) is directly proportional to acceleration (a) and mass (m). This equation reveals that an object’s acceleration is determined by the force applied to it and the object’s mass.
Force: The Driving Force of Motion
What is Force?
Force is an interaction that changes the motion of an object. It can be a push, a pull, or a twist, and it always has both a magnitude and a direction. Without force, objects would remain motionless, forever stuck in their current state.
Newton’s Laws: Force and Acceleration
Sir Isaac Newton discovered three fundamental laws that describe the relationship between force and motion. His second law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. In other words, the greater the force applied to an object, the greater its acceleration, and the greater its mass, the smaller its acceleration.
Types of Force
Force can manifest in various forms:
- Impulse: Force acting over a brief period, causing a sudden change in momentum.
- Weight: The force of gravity pulling an object towards the Earth.
- Pressure: Force distributed over an area, crucial for understanding phenomena like fluid flow and structural stability.
Acceleration: Unveiling the Secrets of Motion’s Evolution
Embark on a captivating journey as we delve into the realm of acceleration, where motion transforms and unveils its hidden secrets. Whether it’s the exhilarating launch of a rocket or the gentle deceleration of a car, acceleration is the driving force behind every change in an object’s motion.
Acceleration is the rate at which velocity changes over time. In other words, it measures the rapidity with which an object speeds up or slows down. Understanding acceleration is crucial to comprehending the dynamics of motion and predicting the behavior of moving objects.
At the core of acceleration lies a mathematical formula:
Acceleration (a) = (Final Velocity (vf)) – (Initial Velocity (vi)) / Time (t)
This equation reveals the relationship between acceleration, the initial and final velocities of an object, and the time taken for the velocity change.
Acceleration is heavily influenced by various factors, including velocity, speed, time, and distance. Velocity, which encompasses both speed and direction, plays a significant role in determining acceleration. An object’s speed alone, however, does not indicate acceleration. Time and distance also come into play. For instance, a car traveling at a constant speed has no acceleration, even though it may cover a significant distance.
Understanding acceleration empowers us to predict how objects will behave under different conditions. For example, knowing the acceleration of a falling object allows us to calculate the time it will take to reach the ground or the distance it will travel in a given interval.
In the world of physics, acceleration is an integral concept that governs the motion of everything around us. It’s the key to unlocking the secrets of motion, from the gentle sway of a pendulum to the mind-boggling speeds of rockets. By unraveling the mysteries of acceleration, we gain a deeper appreciation for the dynamic nature of the universe.
Mass: The Inherent Resistance to Change
Definition and Significance of Mass
Mass is the fundamental property of matter that measures its resistance to acceleration. It represents the quantity of matter within an object. Mass is an intrinsic property, meaning it remains constant regardless of location or environmental conditions.
In everyday life, we associate mass with weight. However, weight is a force that changes depending on gravitational forces, while mass is an immutable characteristic of an object.
Weight, Inertia, and Density
- Weight: Weight is the force exerted by gravity on an object. It depends on its mass and the gravitational field strength at its location. On Earth, the acceleration due to gravity is approximately 9.8 m/s².
- Inertia: Inertia is an object’s resistance to any change in its motion. Mass and inertia are directly proportional; objects with greater mass have greater inertia. Inertia resists changes in velocity, direction, and speed.
- Density: Density is a measure of how closely packed matter is within an object. It is calculated as mass per unit volume. Objects with higher density are typically composed of more tightly packed atoms or molecules.
Understanding Mass
Mass plays a crucial role in various physical phenomena, including:
- Newton’s Second Law: This law states that the force applied to an object is directly proportional to its mass and acceleration (F = ma).
- Momentum: Momentum is a measure of an object’s motion, calculated as mass multiplied by velocity (p = mv).
- Energy: Mass can be converted into energy, as described by Einstein’s famous equation (E = mc²).
In conclusion, mass is a fundamental property of matter that measures its resistance to change. It is related to weight, inertia, and density, and it plays a crucial role in understanding the interactions and motion of objects.
Newton’s Second Law: Force, Mass, and Acceleration
In the realm of physics, the interplay between force, mass, and acceleration is a fundamental principle that governs the motion of objects. Known as Newton’s Second Law, this law provides a mathematical framework for understanding how these three physical quantities influence each other.
The Equation: F = ma
At the heart of Newton’s Second Law lies a simple yet profound equation: F = ma. This equation states that the force applied to an object is directly proportional to its mass and its acceleration. In other words, the more massive an object is, the greater force is required to accelerate it by the same amount. Conversely, the heavier an object is, the less it will accelerate when subjected to the same force.
Derivation and Implications
The equation F = ma can be derived from the fundamental principles of motion. By considering the change in momentum of an object over time, it can be shown that the rate of change in momentum is directly proportional to the force applied.
The implications of this law are vast. It governs the dynamics of everything from the motion of planets in space to the acceleration of cars on Earth. It provides a tool for engineers to design machines and vehicles, and it helps scientists understand the behavior of matter at both macroscopic and microscopic scales.
Real-World Examples
To illustrate the relationship between force, mass, and acceleration, let’s consider a few real-world examples:
- A car pushing a boulder: A car applying a larger force on a boulder will accelerate it faster than a car applying a smaller force.
- A rocket taking off: The massive rocket engines produce a tremendous force, propelling the rocket upward with a significant acceleration.
- A ball thrown into the air: The force of gravity acting on the ball pulls it downward, causing it to accelerate toward the ground.
Momentum: Mass and Velocity in Motion
Momentum: The Essence of Moving Mass
In the realm of physics, momentum emerges as a captivating concept that describes the dynamic interplay between mass and velocity. It quantifies the inertia of an object, its inherent resistance to changes in motion. Momentum unveils the harmonious relationship between mass and velocity, offering insights into the trajectories of moving objects.
Defining Momentum
Momentum, denoted by the symbol p, measures the quantity of motion possessed by an object. Mathematically, it is calculated as the product of an object’s mass (m) and its velocity (v):
p = mv
This equation embodies the fundamental connection between mass and velocity. Greater mass implies greater momentum, while higher velocity translates into increased momentum.
Impulse: The Catalyst for Change
Impulse serves as the catalyst for changes in momentum. It represents the product of force (F) and time (t): J = Ft. Impulse imparts a force over a specific duration, leading to a change in the velocity and therefore the momentum of an object.
The change in momentum is directly proportional to the impulse applied to the object. This relationship is encapsulated in Newton’s second law of motion, which states that the time rate of change of momentum of an object is equal to the net force acting on it:
dp/dt = F
Momentum in Action
Momentum plays a pivotal role in understanding the dynamics of collisions. In an elastic collision, the total momentum of the colliding objects remains conserved, while their kinetic energy may dissipate. Conversely, in an inelastic collision, both momentum and kinetic energy are not conserved due to the conversion of some energy into other forms.
Moreover, momentum underpins the operation of various devices, including rockets, pendulums, and gyroscopes. Rockets, for instance, utilize the principle of momentum conservation to propel themselves through space by expelling high-speed exhaust gases.
Inertia: The Force That Resists Change
Imagine a massive boulder sitting on the ground, seemingly immovable. This resistance to change is a fundamental property of matter known as inertia.
Definition and Concept of Inertia
Inertia is a measure of an object’s reluctance to change its state of motion. It is directly proportional to the mass of the object. Isaac Newton formalized this concept in his First Law of Motion.
Relationship between Mass, Force, and Inertia
The heavier an object is, the more force is required to accelerate or decelerate it. This is because mass provides an object with inertia, making it more resistant to changes in motion.
Resistance to Changes in Motion
Inertia manifests itself in everyday life in various ways. For instance, it takes considerable force to push a heavy object, and a moving object will continue to move in the same direction until an external force acts upon it.
Inertia is a crucial concept in understanding the motion of objects. By considering the inertia of objects, we can better predict their behavior and design solutions to overcome their resistance to change.