Moment Of Inertia: A Comprehensive Guide To Measuring Rotational Resistance
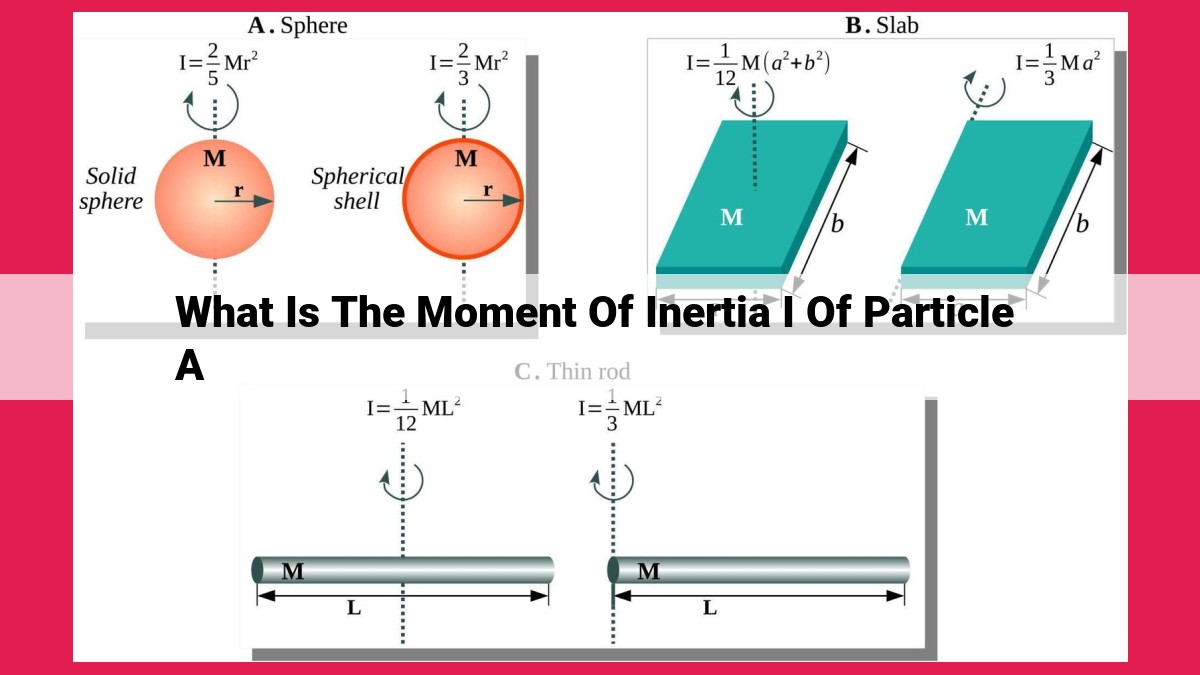
The moment of inertia (I) of particle A is a scalar quantity that measures its resistance to angular acceleration. It depends on the mass (m) of the particle and the distance (r) between its axis of rotation and its center of mass. The formula for calculating I is I = mr^2. The axis of rotation is a reference line about which the particle rotates. A higher moment of inertia indicates a greater resistance to angular acceleration, meaning more force or torque is required to change the particle’s rotational motion.
Understanding Moment of Inertia: A Primer
In the captivating realm of physics, where the interplay of forces and motion shapes our world, there lies a fascinating concept known as moment of inertia. It is a measure that quantifies an object’s resistance to angular acceleration, akin to its resistance to linear acceleration in translational motion.
Understanding the moment of inertia is crucial for comprehending the intricate dance of objects in rotational motion. It allows us to predict their behavior, anticipate their trajectories, and unravel the dynamics of spinning tops, gyroscopes, and celestial bodies alike.
The Concept of a Particle
In the realm of rotational motion, understanding the moment of inertia is paramount. This concept hinges on the properties of particles—point-like objects with mass that serve as the fundamental building blocks of matter.
Defining Particles
A particle is often idealized as a mass concentrated at a singular point. It possesses no physical dimensions or shape, yet it carries a specific mass. This mass is a crucial property as it determines the particle’s resistance to changes in its rotational motion, a concept known as moment of inertia.
Importance of Particle Properties
The mass of a particle is directly proportional to its moment of inertia. This means that heavier particles exhibit greater resistance to changes in their rotational motion. Additionally, the distribution of mass within the particle also plays a role. Particles with mass distributed farther from the axis of rotation experience a larger moment of inertia compared to those with mass concentrated closer to the axis.
The concept of a particle is essential for understanding the moment of inertia, which quantifies an object’s resistance to rotational motion. The mass and distribution of mass within a particle are key factors that determine the value of the moment of inertia. This knowledge is vital for analyzing the rotational motion of complex objects, as their overall moment of inertia is determined by the collective properties of their constituent particles.
The Role of the Axis: Unraveling the Impact on Moment of Inertia
In the realm of rotational dynamics, the axis plays a pivotal role in determining the moment of inertia, a crucial parameter that governs an object’s resistance to angular acceleration. Just as a fulcrum influences the ease of lifting a lever, the axis acts as a rotational reference point.
Imagine a merry-go-round spinning around a central pole. The choice of the axis as the pole significantly affects the moment of inertia, which in turn determines how much force is required to change the merry-go-round’s angular velocity. If we were to shift the axis away from the center, the moment of inertia would increase, making it harder to accelerate or decelerate the rotation.
This is because the moment of inertia is calculated by summing up the product of each particle’s mass and the square of its distance from the axis. When the axis is farther from the particles, this squared distance becomes larger, leading to a higher moment of inertia.
Understanding the role of the axis is crucial for analyzing rotational motion. By carefully selecting the appropriate axis, engineers and physicists can optimize the design of rotating systems, such as turbines, motors, and flywheels, ensuring efficient performance and minimizing energy losses.
Related Concepts: Angular Momentum, Torque, and Rotational Kinetic Energy
- Describe the relationship between moment of inertia, angular velocity, and angular momentum.
- Explain the interaction between moment of inertia and torque in producing angular acceleration.
- Discuss the significance of rotational kinetic energy in quantifying rotational motion.
Understanding the Interplay of Moment of Inertia with Angular Momentum, Torque, and Rotational Kinetic Energy
As we delve deeper into the world of rotational motion, we uncover the intricate relationships between moment of inertia, angular momentum, torque, and rotational kinetic energy. Each of these concepts plays a vital role in shaping the dynamics of spinning objects.
Moment of Inertia and Angular Momentum: A Dynamic Duo
Imagine a spinning flywheel. Its resistance to changes in rotational motion is quantified by its moment of inertia. This resistance is directly proportional to the flywheel’s mass and the distribution of that mass relative to its axis of rotation.
Angular momentum, on the other hand, measures the flywheel’s rotational inertia, or its tendency to keep spinning. The flywheel’s angular velocity, or spin rate, also influences its angular momentum. The greater the moment of inertia or angular velocity, the more angular momentum the flywheel possesses.
Moment of Inertia and Torque: A Force for Acceleration
Torque acts like a force that causes rotational acceleration. When a force is applied to an object with moment of inertia, it generates a torque. The greater the moment of inertia, the smaller the angular acceleration for a given torque. This means that objects with high moment of inertia are more difficult to accelerate.
Conversely, a smaller moment of inertia results in a greater angular acceleration for the same torque. In other words, objects with low moment of inertia are easier to set in motion.
Rotational Kinetic Energy: Quantifying Rotational Motion
Rotational kinetic energy represents the energy of a rotating object due to its motion. It is directly proportional to both the moment of inertia and the square of the angular velocity.
Imagine a spinning top. Its moment of inertia and angular velocity determine its rotational kinetic energy. The faster the top spins or the greater its mass distribution relative to its axis, the higher its rotational kinetic energy.
Moment of inertia, angular momentum, torque, and rotational kinetic energy are intimately interconnected concepts that govern the behavior of rotating objects. Understanding these relationships allows us to analyze and predict the dynamics of rotational systems, from spinning flywheels to orbiting planets.
Calculating Moment of Inertia: The Case of Particle A
In the realm of rotational motion, moment of inertia is a crucial concept that determines an object’s resistance to angular acceleration. It’s like a measure of how hard it is to get something spinning or stop it from spinning.
Imagine a particle, a point-like object with a certain mass. The moment of inertia of this particle depends on two key factors: its mass and the distance from the axis of rotation. The axis is the imaginary line around which the particle rotates. So, the farther the particle is from the axis or the heavier it is, the greater the moment of inertia.
Mathematically, the moment of inertia of a particle A about an axis perpendicular to its motion is given by the formula:
I = mr^2
where:
- I is the moment of inertia
- m is the mass of the particle
- r is the distance from the particle to the axis
This formula tells us that the moment of inertia is proportional to both the mass and the square of the distance from the axis. For instance, if you double the distance from the particle to the axis, you’ll quadruple its moment of inertia.
Understanding the moment of inertia is essential for analyzing rotational motion. It helps us predict how objects will behave when subjected to torques and angular accelerations. So, whether you’re dealing with a spinning top or a rotating celestial body, the moment of inertia is a fundamental concept that sheds light on the intricate world of rotational mechanics.