Understanding Mixed-Degree Systems: Graphical Analysis For Determining Solvability

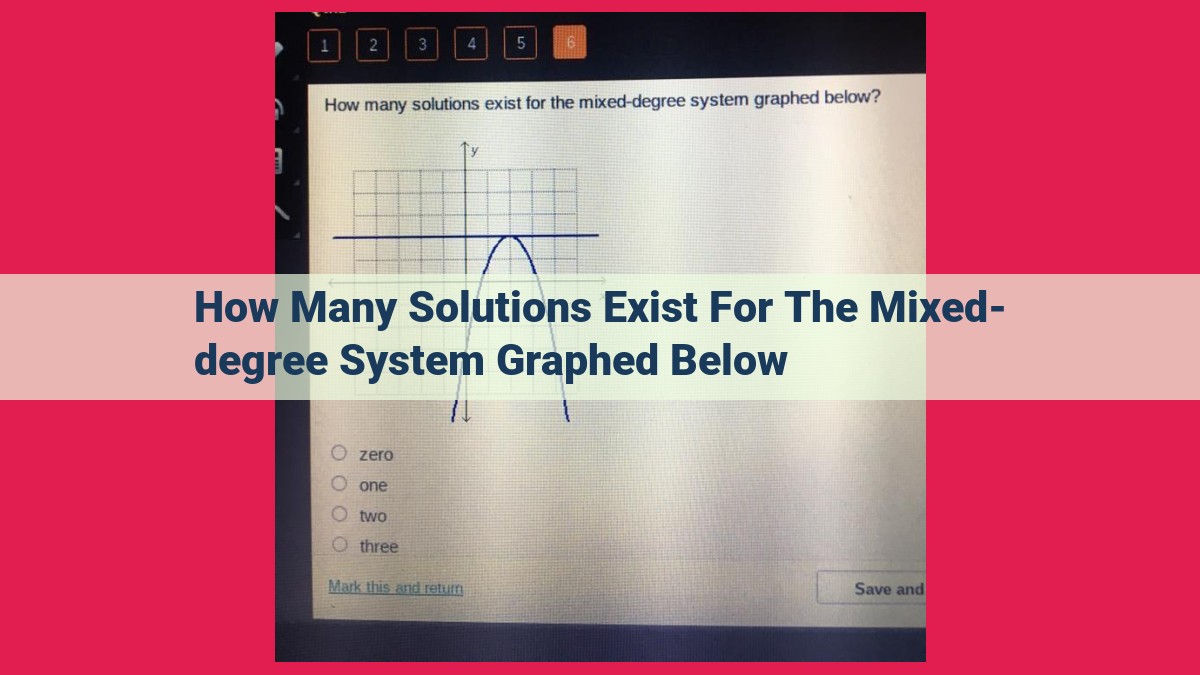
Mixed-degree systems, involving equations of varying degrees, can yield unique, infinite, or zero solutions. By graphing the system, intersection points reveal the number of solutions. If the graphs intersect at a single point, there’s a unique solution. Multiple intersections indicate infinitely many solutions. When there are no intersections, the system has no solution. The graphical representation provides a clear understanding of the relationship between intersection points and the number of solutions, making it crucial for determining the system’s solvability.

Unveiling the Secrets of Mixed-Degree Systems: A Graphical Journey

Are you ready to dive into the intriguing world of mixed-degree systems? These systems, where equations of varying degrees dance together, invite us to embark on a graphical exploration. Let’s uncover their mysteries, step by step.

Defining Mixed-Degree Systems with a Twist:

Mixed-degree systems are like a mathematical puzzle, composed of equations with different exponents. Imagine a mischievous magician waving a wand over a system of linear and quadratic equations, transforming them into a curious mix-match. These systems can be depicted graphically, revealing intricate patterns that hold the key to their solutions.

Navigating the Graphical Landscape:

When it comes to mixed-degree systems, graphs become our allies. By plotting the equations on a coordinate plane, we create a visual representation that unveils their behavior. Intersection points, where the lines or curves meet, hold significant meaning. They determine the number of solutions, providing vital clues to the system’s secrets.

Unveiling the Number of Solutions:

The number of intersection points dictates the destiny of the system. With a single intersection point, a unique solution awaits us. Multiple intersection points beckon us towards infinitely many solutions, opening up a world of possibilities. But beware, systems with no intersection points leave us with a path of no solutions, like a tantalizing riddle left unanswered.

Graphical Representation:

• Explain how to identify intersection points of mixed-degree systems.
• Describe how the number of intersection points determines the number of solutions.

Graphical Representation of Mixed-Degree Systems

Identifying Intersection Points

In mixed-degree systems, where equations are of different degrees (such as linear and quadratic), finding intersection points is crucial. These points represent the solutions of the system, where both equations hold true. To identify them, graph both equations on the same coordinate plane and locate the points where they intersect. These intersections indicate the possible solutions.

Number of Intersection Points and Solutions

The number of intersection points determines the number of solutions to the system. A single intersection point corresponds to a unique solution, meaning there is only one point (x, y) that satisfies both equations. Multiple intersection points indicate infinitely many solutions, since there are an infinite number of points that lie on the intersecting lines or curves. Finally, if there are no intersection points, there are no solutions, indicating that the system is inconsistent and cannot be solved.

Number of Solutions

In the realm of mathematics, when we encounter a mixed-degree system—a perplexing equation where polynomials of varying degrees intertwine—determining the number of solutions becomes a captivating puzzle. Understanding the essence of this concept is crucial for unraveling the mysteries that lie within these intricate systems.

The number of solutions is profoundly influenced by the intersection points between the different degree polynomials. These intersection points are like gateways that reveal the path to finding solutions. Let’s explore the three primary outcomes:

Unique Solutions:

When the intersecting swords of the polynomials cross at precisely one point, it’s a triumph! This solitary intersection signals the existence of a unique solution. Just as a solitary lighthouse guides ships to shore, this singular point illuminates the path to finding the sole answer.

Infinitely Many Solutions:

The mathematical landscape takes a fascinating turn when the polynomial paths collide at multiple points. It’s like a dance of intersecting lines, each step creating a new point of encounter. This harmonious convergence leads to infinitely many solutions. The system becomes a symphony of possibilities, offering an abundance of answers.

No Solution:

Sometimes, the polynomials play a game of hide-and-seek, refusing to meet at any point. In this perplexing scenario, their paths remain parallel, never intersecting. The consequence? No solution. It’s as if the system is a locked door, with no key to unlock its secrets.

Unique Solution

In the realm of mixed-degree systems, where equations of varying degrees dance upon the Cartesian plane, the existence of unique solutions holds a captivating allure. Like the solitary beacon in a stormy sea, a unique solution represents a clear-cut intersection between the curves that define the system.

Imagine a coordinate plane adorned with a quadratic parabola and a linear line. As these curves embark on their journey, their paths intertwine at a single point of intersection. This intersection is the key to unlocking the unique solution to the system.

The reason for this exclusivity stems from the one-to-one correspondence between the curves. The parabola’s smooth arch and the line’s straight ascent create a unique combination that allows for only one point of contact. Unlike systems with multiple intersection points, which lead to infinitely many solutions, the singular intersection here ensures a distinct and solitary solution.

In this delightful scenario, the x-coordinate of the intersection point reveals the root of the equation, the value at which the quadratic expression and linear function align. This pristine solution stands alone, unaffected by any other potential intersections. It is the sole answer, the unambiguous resolution to the mixed-degree system.

So, when you encounter a mixed-degree system that graces the plane with a solitary intersection, embrace the clarity that awaits. A unique solution is within your grasp, a testament to the harmonious dance between the curves that define it.

Infinitely Many Solutions: Where Lines Intertwine

In the realm of mixed-degree systems, when multiple intersection points grace the graph, the world of solutions blooms with infinite possibilities. Envision a scenic path where countless lines intersect, each carrying its own story.

These intersection points represent solutions to the system of equations. Every point where two lines embrace tells a tale of harmony, where the variables dance in perfect balance. When these intersections paint the graph with their presence, it signifies an infinite tapestry of solutions stretching beyond the horizon.

Unlike the solitary star of a unique solution, or the desolate emptiness of no solutions, the symphony of intersection points weaves a vibrant melody of possibilities. Each point offers a unique combination of variable values that satisfies the equations.

It’s as if the graph has transformed into a kaleidoscope, where every twist and turn reveals a new arrangement of solutions. The lines, like mischievous children, intertwine and dance, creating an intricate mosaic of possibilities.

In this realm of infinitely many solutions, the system of equations becomes a gateway to an endless labyrinth of solutions. Each path leads to a different destination, and the journey itself becomes an exploration of mathematical possibilities.

No Solution: A Void of Intersection

In the realm of mixed-degree systems, where equations of varying degrees intertwine, there exists a peculiar scenario where no solution resides. This occurs when the imaginary paths of these equations fail to cross at any point, leaving us with an empty set of solutions.

Imagine a linear equation, a straight line traversing the coordinate plane. Now add a quadratic equation, a graceful parabola. As these lines dance around, they may intersect once, twice, or not at all. In the latter case, the lines of pursuit remain tantalizingly parallel or diverge away, never finding a point of accord.

For a mixed-degree system, this translates to no intersection points. Since the essence of a solution lies at the intersection, the absence of these crossings renders the system void of solutions. It’s a mathematical ballet where the dancers gracefully evade each other, leaving behind a silent symphony of zeros.

This no-solution zone may arise from several factors. Perhaps the equations represent two parallel lines, forever chasing but never meeting. Or it could be a lone parabola soaring high above the linear equation’s reach, leaving it stranded in isolation.

Whatever the cause, the message is clear: no intersection, no solution. It’s a mathematical paradox, a tantalizing void where potential solutions vanish into the ether, a testament to the capricious nature of equations.