Understanding Difference In Mathematics: Subtraction, Numerical Gap, And Inverse Operations

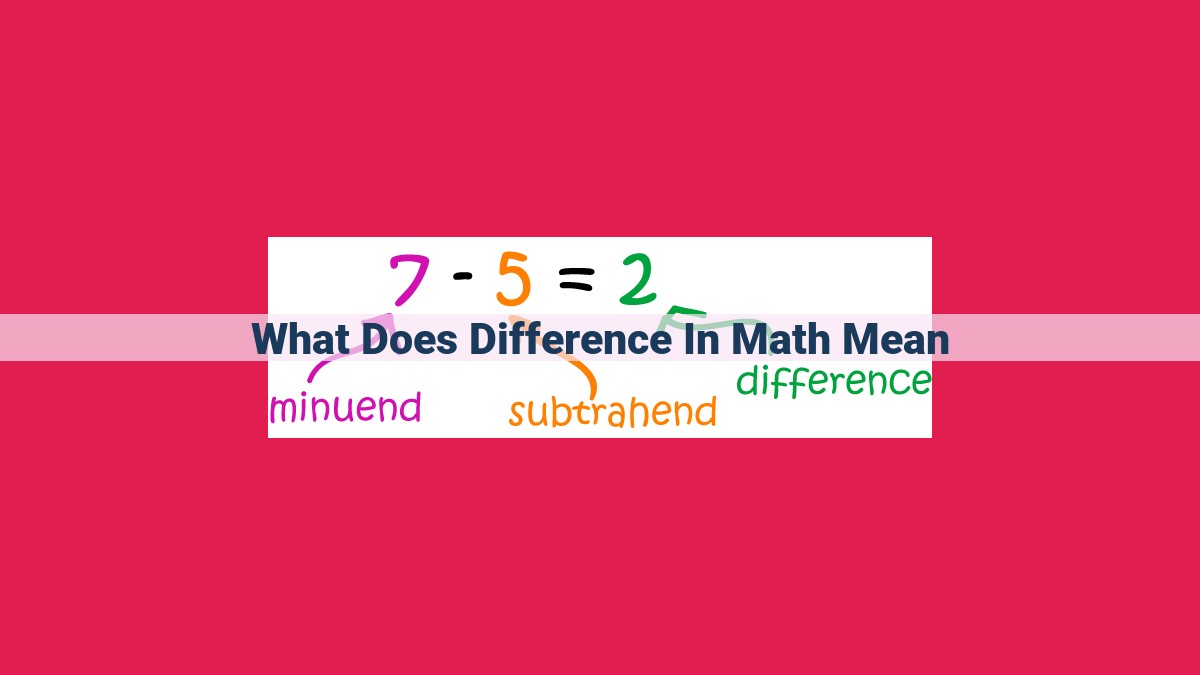
In mathematics, “difference” refers to the result obtained by subtracting one number from another. This operation is formally known as subtraction and is represented by the minus sign (-). Differences highlight the numerical gap between the two numbers, with a positive difference indicating that the first number is greater and a negative difference indicating the opposite. Negative numbers arise when subtracting a larger number from a smaller number, and the inverse property of subtraction states that subtracting and then adding the same number results in the original number. Opposites, or additive inverses, are numbers that cancel each other out when added, further reinforcing the inverse relationship in subtraction.

Understanding the Difference in Mathematics

In the realm of mathematics, the concept of “difference” plays a pivotal role, enabling us to quantify the variation between two quantities. It represents the numerical gap between two values, helping us compare and contrast their magnitudes.

Finding Differences

In everyday scenarios, we encounter differences constantly. For instance, calculating the difference in time between two appointments allows us to plan our schedules effectively. Similarly, determining the difference in height between two buildings showcases their relative grandeur. These examples demonstrate how differences help us understand the magnitude and direction of change.

Subtraction: The Mathematical Tool for Finding Differences

Within the mathematical framework, the operation of subtraction serves as the essential tool for finding differences. When we subtract one number from another, we are essentially calculating the numerical distance between them. This process reveals the extent to which one value exceeds or falls short of the other.

Negative Numbers and Subtraction

In certain instances, subtraction can result in negative numbers. This occurs when the number being subtracted is larger than the number from which it is being taken. Negative numbers represent values less than zero and signify the opposite of the original value. Understanding negative numbers is crucial for grasping the concept of difference in mathematics.

Inverse Property of Subtraction

Furthermore, subtraction possesses an important property known as the inverse property. According to this property, if we subtract a number from another number and then add that same number back, we obtain the original number. This property serves as a powerful tool for solving equations and simplifying expressions.

Opposites as Inverse Numbers

In the mathematical world, opposites represent pairs of numbers that are inverses of each other. When we add one number from a pair of opposites, we effectively cancel out the effect of the other. This demonstrates the close relationship between inverse operations and the inverse property.

Understanding the Essence of Subtraction: Unraveling the Mathematics of Difference

In the realm of mathematics, the concept of “difference” holds immense significance. It forms the cornerstone of countless mathematical operations, calculations, and applications. But what exactly is difference in mathematics?

Subtraction: The Key to Unlocking Difference

The primary way we determine the difference between two numbers is through the operation of subtraction. In subtraction, we take a larger number and subtract a smaller number from it, resulting in a new value that represents the difference.

Example:

If we subtract 7 from 10, we get 3. In this case, 3 is the difference between 10 and 7.

Subtraction is inextricably linked to the concept of negative numbers. When we subtract a larger number from a smaller number, the result becomes negative. This is because the final value indicates how much less the smaller number is compared to the larger number.

Example:

If we subtract 8 from 5, we get -3. This signifies that 5 is 3 less than 8.

The Inverse Property: A Mathematical Symmetry

Subtraction boasts a unique property known as the inverse property. This property states that if we subtract a number from another number and then add it back, we return to the original number.

Mathematically:

a - b + b = a

This property proves invaluable in solving equations and simplifying expressions, as it allows us to manipulate numbers while maintaining balance.

Opposites: Numbers with a Special Relationship

In mathematics, we encounter numbers known as opposites. Opposites are numbers that are inverses of each other, meaning that when we add them, the result is always 0.

Example:

3 and -3 are opposites because 3 + (-3) = 0.

Opposites play a crucial role in understanding inverse operations and the inverse property. They represent numbers that are different but also complementary, balancing each other out in the mathematical landscape.

By grasping the concepts of subtraction, negative numbers, inverse operations, and opposites, we unravel the tapestry of difference in mathematics. It is through this understanding that we unlock the power of mathematical calculations and applications, empowering us to navigate the world of numbers with confidence.

Negative Numbers: The Result of Subtraction Unveiled

In the realm of mathematics, the concept of “difference” is fundamental. It’s the essence of subtraction—the operation that unveils the gap between two numbers. When the numbers involved are on equal footing, their difference can be both positive or negative. But what happens when a larger number takes the stage, leaving the smaller number in its wake? The outcome can be a mathematical enigma: a negative number.

Negative Numbers: A Departure from the Positive

In the realm of mathematics, positive numbers reign supreme. They represent quantities that are present, tangible, and have a definitive magnitude. Negative numbers, on the other hand, venture into uncharted territory. They symbolize the absence of something or the existence of an opposite force.

The birth of a negative number is a direct consequence of subtraction. When a larger number is subtracted from a smaller one, it’s as if the missing quantity is being represented by a negative value. For example, if we subtract 5 from 2, the result is -3. This negative number indicates that the original quantity of 2 is now 3 units less.

Navigating the World of Negative Numbers

Embracing negative numbers requires a shift in perspective. They challenge our intuition but unlock a deeper understanding of the mathematical world. Negative numbers are not just mathematical oddities; they are essential tools for representing and manipulating quantities that extend beyond our immediate experience.

Negative numbers, born from the subtraction of a larger number from a smaller, are indispensable components of the mathematical landscape. Understanding their significance paves the way for a more comprehensive grasp of mathematics, enabling us to navigate its complexities with confidence and unravel the mysteries that lie within.

The Inverse Property of Subtraction: Unlocking Mathematical Magic

Imagine yourself on a mathematical journey, where numbers dance and equations whisper secrets. Along this path, you’ll encounter a remarkable property that will guide your steps – the inverse property of subtraction.

In the world of mathematics, subtraction is the operation that unveils the difference between two numbers. However, the inverse property of subtraction reveals a hidden power that allows us to reverse the operation and recover the original numbers.

Formally, the inverse property states: if you subtract a number and then add it back, you miraculously return to the starting number. It’s like taking a step forward and then taking a step back, landing exactly where you began.

This property is an invaluable tool in the mathematical toolbox. It helps us unravel equations and simplify expressions. For instance, if you have an equation like “x – 5 = 10,” the inverse property tells us that adding 5 to both sides will bring balance and reveal the value of x: “x – 5 + 5 = 10 + 5,” which simplifies to “x = 15.”

Moreover, the inverse property is deeply intertwined with the concept of opposites. In mathematics, opposites are numbers that, when added together, cancel each other out. The inverse property highlights this connection by demonstrating that subtracting a number and then adding its opposite results in the original number.

In essence, the inverse property of subtraction is a mathematical enchantment that allows us to navigate the world of numbers with ease and precision. It’s a fundamental concept that empowers us to solve equations, simplify expressions, and unravel the mysteries of mathematics with confidence.

Opposites as Inverse Numbers: Unraveling the Secrets of Subtraction

In the realm of mathematics, the concept of difference plays a fundamental role. It’s a concept that we encounter everywhere, from calculating the gap between two numbers to understanding the complexities of negative numbers.

Subtraction: The Difference-Maker

Subtraction is the mathematical operation that determines the difference between two numbers. When we subtract, we’re essentially asking, “What number do we need to add to the smaller number to get the larger number?“

For instance, if we have 10 apples and give 5 away, the difference between what we had and what we have now is 5. This difference represents the number of apples we’ve subtracted.

Introducing Negative Numbers: The Result of Subtraction

Sometimes, when we subtract a larger number from a smaller number, we end up with a negative result. This is because in mathematics, negative numbers exist to represent values less than zero.

When we encounter a negative difference, it means that the smaller number was less than the larger number. For example, if we have -5 apples, it means we have 5 apples less than zero.

Inverse Property of Subtraction: Undoing the Difference

Mathematics is all about relationships, and subtraction has a unique relationship with addition. In particular, the inverse property of subtraction states that if we subtract a number and then add it back, we get the original number.

For instance, if we start with 10 and subtract 5, we get 5. If we then add 5 back, we get back to our original number, 10. This property is crucial for solving equations and simplifying expressions.

Opposites: The Inverse Partners

In the mathematical world, opposites are numbers that are inverses of each other. They represent the same distance from zero but on opposite sides of the number line. For example, 5 and -5 are opposites.

Opposites relate to inverse operations and the inverse property. When we add the opposite of a number, we’re effectively undoing the addition. Similarly, when we subtract the opposite of a number, we’re undoing the subtraction.

Understanding the concept of difference in mathematics is essential for success in the subject. It helps us compare numbers, solve equations, and navigate the complexities of negative numbers. By embracing the power of difference, we unlock a world of mathematical exploration and problem-solving.