Mastering Segment Length Calculations: Essential For Geometry And Stem Careers
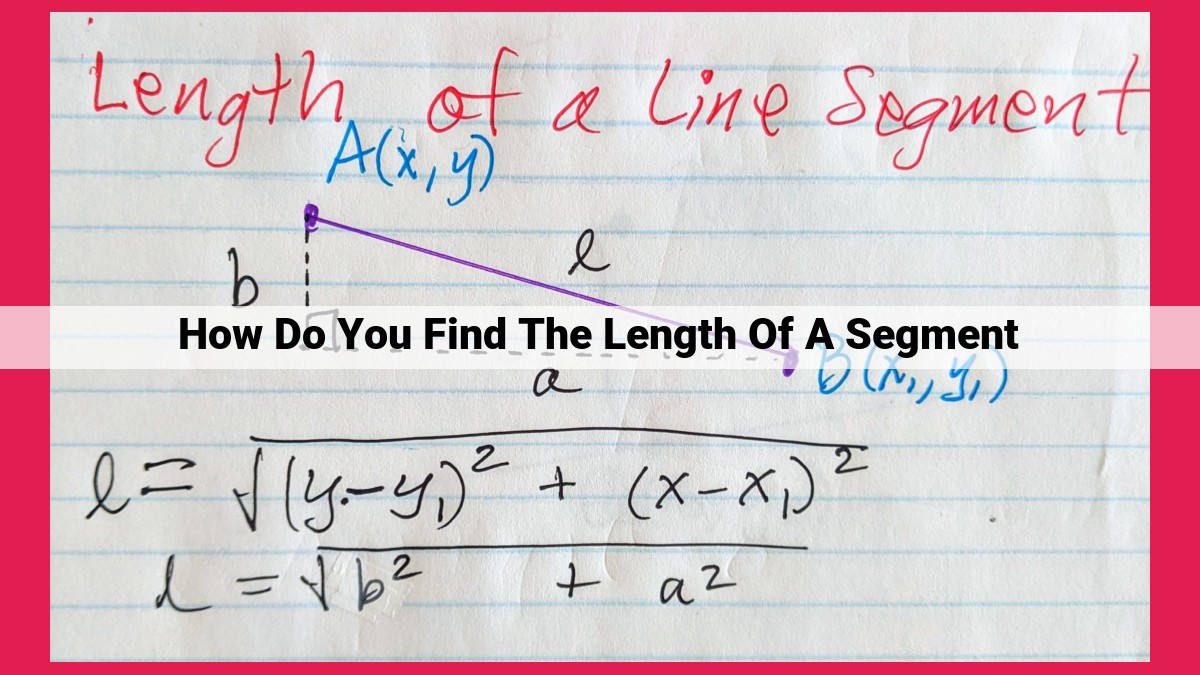
Finding segment lengths is crucial in geometry and practical fields. The distance formula calculates distances between points, while the Pythagorean theorem determines lengths in right triangles. The Segment Addition Postulate measures composite segments. Coordinate geometry uses these concepts with coordinates. These methods are indispensable in architecture, engineering, and design, highlighting the importance of mastering segment length calculations for success in geometry and beyond.
The Importance of Segment Length: Unlocking Geometry and Real-World Applications
In the realm of geometry, understanding segment length is pivotal. From intricate mathematical calculations to practical applications in our daily lives, the ability to determine the length of segments empowers us to navigate the world around us.
Segment length plays a fundamental role in the field of architecture. Architects rely on precise measurements to design and construct structures that are both aesthetically pleasing and structurally sound. Engineers harness this knowledge to calculate the load-bearing capacity of bridges, ensuring the safety of our infrastructure. In the world of product design, designers utilize segment length to create visually appealing and functional objects, from sleek smartphones to ergonomic chairs.
Beyond the realms of geometry and engineering, segment length finds practical use in everyday activities. Hikers measure trail distances to plan their journeys, while pilots use precise measurements to navigate their aircrafts. Astronauts rely on accurate calculations of segment lengths when docking with the International Space Station, seamlessly connecting modules in the vast expanse of space.
By mastering the art of finding segment lengths, we unlock a world of possibilities. Whether we are exploring the intricacies of geometry, designing buildings, or embarking on adventures, a solid understanding of this fundamental concept empowers us to make informed decisions, solve problems, and create a more precise and predictable world.
Distance Formula: The Key to Unraveling Segment Lengths
In the realm of geometry, finding the length of segments is akin to deciphering a riddle, and the distance formula serves as the master key. This formula empowers us to calculate the distance between any two points in a Cartesian plane, unlocking the secrets of segment lengths with unparalleled ease.
Drawing its inspiration from the revered Pythagorean theorem and the Segment Addition Postulate, the distance formula weaves together these fundamental principles to unveil the true nature of segments. Let’s unravel the mysteries one by one:
The Distance Formula in Action:
Imagine two points, A and B, dancing across the Cartesian plane, separated by an unknown distance. The distance formula, a mathematical sorcerer, transforms their coordinates into a measure of their separation. It reads:
Distance = √((x2 - x1)^2 + (y2 - y1)^2)
where (x1, y1) and (x2, y2) represent the coordinates of points A and B, respectively.
Pythagorean Theorem: The Building Block:
The Pythagorean theorem plays a pivotal role in the distance formula, providing the foundation for understanding the relationship between the sides of a right triangle. This theorem states that in a right triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides:
a^2 + b^2 = c^2
where a and b represent the lengths of the two shorter sides, and c represents the length of the hypotenuse.
Segment Addition Postulate: Connecting the Dots:
The Segment Addition Postulate extends the distance formula’s reach, enabling us to measure the total length of a segment composed of smaller segments. It postulates that the total length of a segment is equal to the sum of the lengths of its constituent segments.
So, there you have it – the distance formula and its accomplice theorems, the Pythagorean theorem and Segment Addition Postulate, illuminating the path to mastering segment length calculations. With these tools at your disposal, you’re well-equipped to unlock the secrets of geometry and conquer any segment length challenge that comes your way.
The Pythagorean Theorem: Unlocking the Secrets of Right-Angled Segments
In the world of geometry, segment length is a fundamental measurement that holds immense importance. From navigating the intricate web of geometric figures to tackling practical applications in engineering and design, the ability to find segment lengths with precision is a cornerstone of mathematical knowledge.
One of the most powerful tools in our geometric arsenal is the Pythagorean theorem. This theorem, attributed to the ancient Greek mathematician Pythagoras, provides a profound method for calculating the length of segments in right triangles.
Consider a right triangle, a triangle with one right angle (90 degrees). The Pythagorean theorem states that for any right triangle with legs of length a and b and hypotenuse of length c, the following equation holds true:
a^2 + b^2 = c^2
This equation allows us to determine the length of any one side of a right triangle, given the lengths of the other two sides. For example, if we know the lengths of the two legs, we can find the length of the hypotenuse by applying the Pythagorean theorem:
c = sqrt(a^2 + b^2)
Or, if we know the length of the hypotenuse and one leg, we can find the length of the other leg using the same equation:
a = sqrt(c^2 - b^2)
b = sqrt(c^2 - a^2)
The Pythagorean theorem is an indispensable tool for solving countless geometric problems. It finds applications in a wide range of disciplines, including architecture, engineering, navigation, and surveying. Mastering this theorem is essential for anyone seeking to excel in mathematics and its practical applications.
Segment Addition Postulate: Measuring Composite Segments
A Story of Measuring the Unexpected
Imagine you’re an architect tasked with designing a magnificent new building. As you sketch the blueprints, you encounter a series of segments that need to be measured precisely. But these segments aren’t simple; they’re composite, made up of smaller segments. How do you determine their total length? Enter the Segment Addition Postulate.
The Segment Addition Postulate Unveiled
Just like its name suggests, the Segment Addition Postulate states that the length of a segment composed of smaller segments is equal to the sum of the lengths of the smaller segments. In other words, if you have a segment AB that is made up of segments AC and CB, then the length of AB is simply AB = AC + CB.
Practical Applications in the Real World
This might seem like a simple concept, but its practical applications are endless. Architects use it to calculate the total length of walls, engineers to determine the distance between points in a structure, and designers to create balanced and visually pleasing compositions.
Real-World Example: The Grand Staircase
Consider the grand staircase in a majestic palace. The staircase is composed of several steps, each with its own length. To determine the total height of the staircase, you can use the Segment Addition Postulate. Simply measure the length of each step and add them together to get the overall height.
The Power of Simplicity
The Segment Addition Postulate may seem like a straightforward concept, but it’s a cornerstone of geometry and practical applications. By understanding how to measure composite segments, you’re equipped to tackle complex problems with confidence and accuracy.
Coordinate Geometry: Unraveling Segment Lengths
Delving into the World of Coordinates
Your journey into the realm of segment lengths takes an exciting turn as we explore the world of coordinate geometry. Here, numbers and coordinates paint a vivid picture of the world around us, enabling us to pinpoint and measure even the most intricate of segments.
Harnessing the Power of the Distance Formula
At the heart of coordinate geometry lies the Distance Formula, a powerful tool that unlocks the secret of finding distances between any two points in a coordinate plane. This formula breathes life into the Pythagorean theorem and the Segment Addition Postulate, empowering us to calculate segment lengths with precision.
Embracing the Pythagorean Theorem
For right-angled segments, the Pythagorean theorem reigns supreme. This time-honored formula unveils the relationship between the lengths of the sides of a right triangle, offering a straightforward method for determining the length of the segment representing the triangle’s hypotenuse.
Unveiling the Segment Addition Postulate
The Segment Addition Postulate extends our reach beyond individual segments, allowing us to conquer the challenge of measuring composite segments—those composed of smaller segments connected end-to-end. This postulate empowers us to add the lengths of these smaller segments, revealing the total length of the composite segment.
Applying Coordinate Geometry in Practice
The allure of coordinate geometry lies in its versatility, extending beyond the confines of theoretical concepts. In the realm of architecture, engineers harness the power of coordinates to plan buildings and structures with precision. Designers rely on this knowledge to create captivating visual compositions, while navigators utilize it to chart their courses through the world.
Mastering Segment Length Calculations
As you delve deeper into the captivating world of geometry, the ability to find segment lengths becomes an indispensable tool. It unlocks the secrets of shape and dimension, empowering you to tackle complex problems with confidence. Embrace the challenge, master these techniques, and witness your understanding of geometry soar to new heights.
Applications: Beyond the Basics
In the realm of architecture, engineers and designers rely heavily on the ability to calculate segment lengths. When drafting blueprints for buildings and structures, precise measurements are essential to ensure structural integrity and aesthetic appeal.
Imagine an architect tasked with designing a new skyscraper. To determine the optimal placement of windows and other architectural features, they need to accurately calculate the length of each segment in the building’s façade. Using the Pythagorean theorem and distance formula, they can ensure that the vertical segments supporting the structure are equidistant and that the horizontal segments forming the floors are parallel and level.
In engineering, segment lengths play a vital role in designing and constructing bridges, roads, and other infrastructure. Engineers use coordinate geometry to determine the shortest distance between two points on a map. This information is crucial for optimizing the placement of roads and bridges, ensuring efficient transportation and minimal environmental impact.
Aerospace engineers rely on segment lengths to calculate the trajectories of rockets and airplanes. By applying the Pythagorean theorem and distance formula, they can determine the exact distance traveled by a spacecraft and the optimal angle for launch. These precise measurements are essential for ensuring the safe and successful completion of space missions.
The ability to find segment lengths is not just confined to the realm of professionals. In everyday life, we encounter countless situations where this geometric knowledge comes in handy. From estimating the distance to the grocery store to measuring the length of fabric for a new curtain, the ability to calculate segment lengths enhances our problem-solving skills and makes us more efficient in our daily tasks.