Mastering Power Series: A Comprehensive Guide To Analysis And Applications

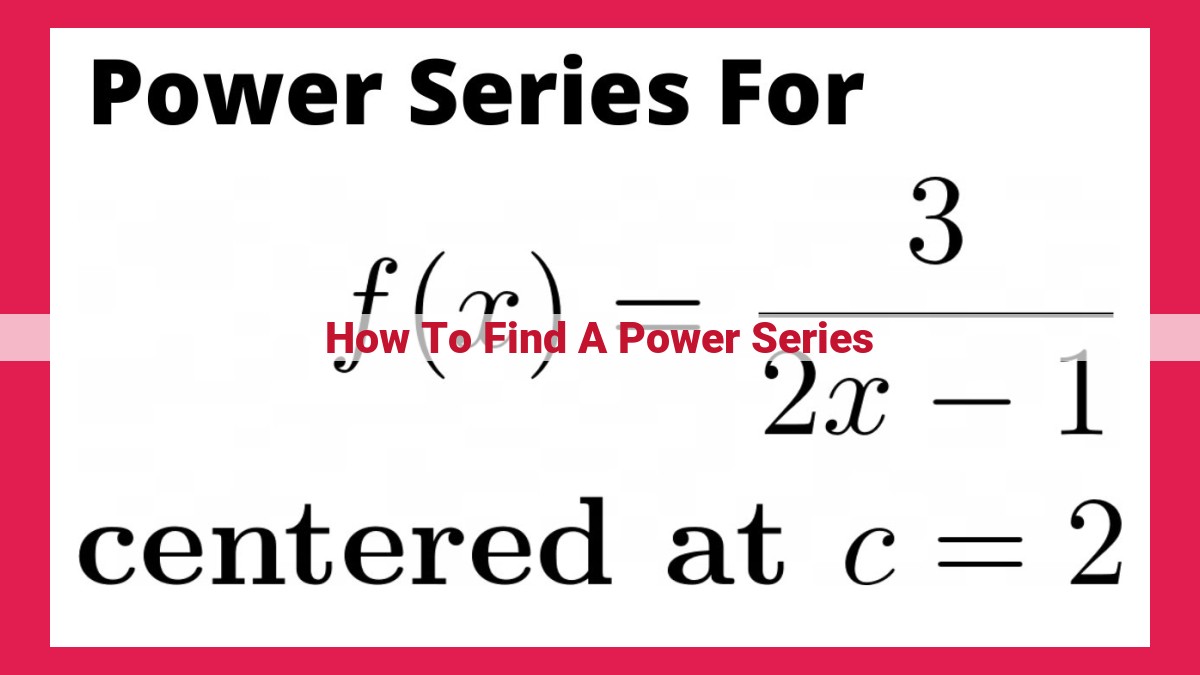
To find a power series representation of a function, consider its Maclaurin series or Taylor series. Use the derivative-based formulas to derive the series and determine the interval of convergence using the Ratio Test or Root Test. Additionally, integrate or differentiate term by term to find the power series for integrals or derivatives. By representing functions as power series, you can approximate complex expressions with infinite sums for analysis and problem-solving in various fields like calculus, science, and engineering.

• Definition and significance of power series
• Types of power series: Maclaurin series and Taylor series

Unlocking the Power of Power Series: An Introductory Guide

In the realm of mathematics, where precision and elegance intertwine, power series emerge as a formidable tool for representing functions as an infinite sum of terms. This blog post aims to guide you through the captivating world of power series, revealing their essence, significance, and applications.

Defining Power Series: A Mathematical Tapestry

At its core, a power series is an infinite series of terms that feature a variable raised to increasing powers. These terms are found in a specific pattern, which can be expressed in the following mathematical notation:

f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + ... + a_nx^n + ...

Here, each coefficient a represents a constant value, and x is the variable. The coefficients and the variable may be real or complex numbers, allowing power series to capture the intricacies of a wide range of functions.

Types of Power Series: Maclaurin and Taylor

Within the realm of power series, two prominent types emerge: Maclaurin series and Taylor series. These variants are distinguished by the point around which they are centered.

• Maclaurin Series: This type of power series is centered at x = 0, making it particularly useful for representing functions that can be approximated around the origin.

• Taylor Series: On the other hand, the Taylor series is centered at any given point x = c. This versatility allows it to represent functions around any desired value, providing more flexibility in approximating functions at specific points.

Applications of Power Series: A Mathematical Toolkit

Power series find widespread applications across various mathematical disciplines and scientific fields. Some prominent use cases include:

• Approximating Functions: Power series offer a powerful method for approximating complex functions as a sum of simpler terms. This technique is used in calculus for finding Taylor series approximations, which can simplify the evaluation of derivatives and integrals.

• Solving Differential Equations: Power series play a crucial role in solving linear differential equations. By representing the solution as a power series, it becomes possible to find solutions that satisfy given boundary conditions.

• Numerical Analysis: In numerical analysis, power series are employed in techniques such as orthogonal polynomials and quadrature methods. These methods aid in approximating solutions to complex mathematical equations.

Benefits of Using Power Series:

• Enables precise representation of complex functions as an infinite sum of simpler terms.
• Provides a gateway to understanding the behavior of functions around specific points.
• Facilitates the approximation of functions for numerical analysis and other applications.
• Paves the way for solving differential equations and other complex mathematical problems.

Maclaurin Series: A Gateway to Function Approximation

In the realm of mathematics, power series play a pivotal role in representing functions as infinite sums of terms. Among these series, the Maclaurin series holds a special significance. Named after the renowned Scottish mathematician Colin Maclaurin, it provides a powerful tool for approximating functions around a specific point.

Formula and Derivation

The Maclaurin series expansion of a function f(x) about the point x = 0 is given by the formula:

f(x) = f(0) + f'(0)x + (f''(0)/2!)x^2 + (f'''(0)/3!)x^3 + ...

where f'(0), f”(0), f”'(0), … represent the derivatives of f(x) evaluated at x = 0.

The derivation of the Maclaurin series involves applying repeated differentiation to f(x) and then setting x to 0. This process effectively captures the behavior of f(x) in the vicinity of x = 0 and represents it as a polynomial series.

Properties and Related Concepts

The Maclaurin series possesses several notable properties:

• Convergence: The Maclaurin series for a function converges within an interval centered at x = 0. The radius of convergence, denoted by R, determines the size of this interval.
• Approximation: The Maclaurin series provides an approximation of f(x) for values of x within the interval of convergence.
• Taylor Series: The Maclaurin series is a special case of the Taylor series, which provides a more general expansion of functions around any given point a.

Interval of Convergence and Radius of Convergence

The interval of convergence for the Maclaurin series is determined using the Ratio Test or Root Test. These tests analyze the behavior of the terms of the series and establish the range of x values for which the series converges. The radius of convergence is half the length of the interval of convergence.

By understanding the Maclaurin series, its formula, properties, and related concepts, we gain a powerful tool for approximating functions, solving problems in calculus and engineering, and gaining deeper insights into the behaviors of mathematical functions.

Taylor Series: Unlocking Infinite Possibilities

When it comes to functions, the Taylor series is a powerful tool that allows us to represent them as an infinite sum of terms. It’s like a magical formula that unlocks the secrets hidden within complex expressions.

Formula and Derivation

The Taylor series is derived using the concept of derivatives. Starting with the function f(x), we take its derivatives f'(x), f''(x), f'''(x), and so on. Each derivative is evaluated at a specific point, usually a, called the center of expansion.

These derivatives are then used to build the Taylor series formula:

f(x) = f(a) + f'(a)(x - a) + f''(a)(x - a)^2/2! + f'''(a)(x - a)^3/3! + ...

This formula represents the function f(x) as an infinite sum of terms, where each term involves a derivative evaluated at a and a power of x - a.

Properties and Applications

The Taylor series is not just a fancy formula. It comes with a treasure chest of properties and applications that make it indispensable in calculus and beyond:

• Approximation of Functions: The Taylor series allows us to approximate functions with high accuracy. By truncating the series after a certain number of terms, we can get a polynomial that closely resembles the function over a specific interval.

• Finding Taylor Series of Derivatives and Integrals: Once we have the Taylor series of a function, we can easily find the Taylor series of its derivatives and integrals. This property simplifies complex calculations and opens up new possibilities for solving problems.

Examples in Action

To illustrate the power of the Taylor series, let’s consider the function e^x. Using the Taylor series formula, we can derive its expansion:

e^x = 1 + x + x^2/2! + x^3/3! + x^4/4! + ...

This series converges for all values of x, giving us an accurate approximation of e^x for any input.

Another example is the trigonometric function sin(x). Its Taylor series expansion is:

sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...

This series also converges for all x, allowing us to approximate sin(x) with polynomial functions.

The Taylor series is a versatile mathematical tool that empowers us to understand and manipulate functions in unprecedented ways. By representing functions as infinite sums of terms, it unlocks new avenues for problem-solving and approximation techniques. Its applications extend far beyond calculus, touching fields like science, engineering, and numerical analysis. So, the next time you encounter a complex function, remember the power of the Taylor series and let it guide you to new frontiers of mathematical discovery.

Power Series: Unlocking the Convergence Zone

In the realm of mathematics, a power series reigns supreme, a formidable tool for representing intricate functions as an infinite sum of terms. These series can take two distinct forms: the Maclaurin series and the Taylor series.

Just like a river has its banks, power series have their own boundaries for convergence. This is where the concepts of interval of convergence and radius of convergence step into the spotlight.

The Interval of Convergence: Defining the Riverbanks

The interval of convergence is the range of values for which a power series converges. To determine this range, mathematicians employ the Ratio Test or the Root Test.

Ratio Test: If the limit of the ratio of consecutive terms in the series is less than 1, the series converges.

Root Test: If the limit of the nth root of the absolute value of each term in the series is less than 1, the series converges.

The Radius of Convergence: Finding the River’s Width

The radius of convergence is the distance from the center of the interval of convergence to its endpoints. It provides a simple way to gauge the range of convergence for a given power series.

Formula for Radius of Convergence:

R = lim (|a_n+1/a_n|)

Where:

• a_n: coefficients of the power series

Ensuring Convergence: Tips for Navigating the River

To guarantee the convergence of a power series, it’s crucial to evaluate both the interval and radius of convergence. This ensures that you’re working within the safe zone where the series exhibits predictable behavior.

By understanding these concepts, you’ll unlock the power of power series, enabling you to tackle complex functions, derive approximations, and solve problems in calculus, science, and engineering with newfound confidence.

Convergence Tests (Ratio Test and Root Test):

• Methods for determining whether a power series converges or diverges

Convergence Tests: Assessing the Destiny of Power Series

In the realm of mathematics, we often encounter power series, intriguing sequences of terms that can represent intricate functions. However, not all power series are created equal; some dance gracefully towards convergence, while others stumble into divergence. Determining the fate of a power series is crucial for its usefulness.

Ratio Test: A Beacon of Convergence

Among the tools used to assess convergence is the Ratio Test. Like a vigilant sentry, it examines the ratio of two consecutive terms in the series, a_n+1/_a_n. If this ratio approaches a value less than 1 as _n reaches infinity, the series converges. It’s like a gentle whisper that promises a harmonious ending.

Root Test: A Sharp Sword of Convergence

Should the Ratio Test falter, the Root Test stands ready, its blade gleaming. This test challenges the series by taking the nth root of its general term, a_n^(1/n). If this root approaches a value less than 1 as n grows large, the series again converges. It’s a more potent weapon, but also more susceptible to convergence_ when the root_ is exactly 1.

Diving into the Convergence Tests

These convergence tests are indispensable allies for mathematicians and scientists alike. They provide a beacon of hope in the murky waters of infinite series, illuminating the path towards convergence or divergence. With their guidance, we can discern whether a power series will dance towards an elegant limit or falter into chaos.

By understanding these tests, we unlock the power to analyze and manipulate power series, harnessing their ability to represent complex functions and solve intricate problems. They become our eyes into the realm of infinite sequences, revealing the hidden patterns and symmetries that govern their behavior.

Integration and Differentiation of Power Series:

• Techniques for integrating and differentiating power series term by term
• Applications in finding Taylor series of integrals and derivatives

Integrating and Differentiating Power Series: A Gateway to Mathematical Exploration

In the realm of mathematics, power series play a pivotal role as tools for approximating functions and unlocking their behavior through integration and differentiation. By manipulating these infinite sums, we gain insights into the intricate workings of the functions they represent.

When integrating a power series, we simply integrate each term individually. This seemingly straightforward process yields remarkable results, enabling us to represent the integral of a function as a new power series. This technique proves particularly useful in situations where the original function lacks an elementary antiderivative.

Differentiation of power series follows a similar principle. We differentiate each term separately, resulting in a new power series that represents the derivative of the original function. This operation allows us to determine the rate of change of a function at specific points and lays the foundation for finding Taylor series of derivatives.

These techniques of integration and differentiation find wide applications in the field of calculus, science, and engineering. By expressing functions as power series, we can approximate their values numerically, analyze their convergence behavior, and solve complex problems with greater ease.

So, embark on this mathematical journey with us, where power series integration and differentiation will illuminate the hidden complexities of functions, empowering you with new tools to navigate the boundless world of mathematics.

Representing Functions as Power Series:

• Approximating functions as infinite sums of terms
• Using power series to represent functions with complex expressions

Representing Functions as Power Series: A Gateway to Exact Approximations

In the realm of mathematics, power series emerge as an invaluable tool for representing functions with remarkable precision. These infinite sums of terms allow us to approximate functions as closely as desired, even when their exact expressions defy easy computation.

Power series grant us the ability to approximate complex functions as sums of simpler terms, opening up a world of possibilities in numerical analysis and approximation techniques. Functions with intricate algebraic expressions, for instance, can be represented as power series, enabling us to evaluate them with greater accuracy and efficiency.

The power of representing functions as power series extends even further. By utilizing Maclaurin or Taylor series, we can approximate derivatives and integrals of functions. This remarkable capability finds widespread applications in calculus, science, and engineering, where precise approximations are crucial for problem-solving.

Practical Implications and Everyday Applications

The practical implications of representing functions as power series are far-reaching. In numerical analysis, for instance, power series are employed to develop efficient numerical methods for solving complex equations and approximating solutions to mathematical problems.

Beyond the realm of academia, power series play a pivotal role in numerous scientific and engineering disciplines. They enable scientists and engineers to model physical phenomena, analyze data, and design systems with greater precision and accuracy.

Representing functions as power series serves as a powerful bridge between theoretical mathematics and real-world applications. By approximating functions as infinite sums of terms, we gain unprecedented flexibility and accuracy in problem-solving. The ability to work with complex functions in a simplified manner empowers us to tackle a wide range of mathematical, scientific, and engineering challenges with newfound confidence and precision.

Unlocking the Power of Power Series: Applications in the Real World

In the realm of mathematics, power series offer an invaluable tool for representing functions as infinite sums of simpler terms. Their versatility extends beyond theoretical concepts to practical applications in numerous fields, including calculus, science, and engineering.

Solving Complex Problems with Calculus

Power series empower us to tackle complex calculus problems with ease. By leveraging the technique of Taylor series, we can approximate functions as polynomials, making integration and differentiation a breeze. This approach proves particularly useful in scenarios where direct methods may fall short.

Numerical Analysis and Approximation Techniques

In the field of numerical analysis, power series serve as a cornerstone for developing approximation techniques. By truncating infinite series at appropriate terms, we can derive accurate approximations for intricate functions. This has applications across disciplines, including computer science and statistics.

The Power of Power Series in Science and Engineering

Power series also play a pivotal role in science and engineering. In physics, they serve as a foundation for understanding phenomena such as wave propagation and quantum mechanics. In engineering, they aid in solving partial differential equations, which are crucial for analyzing complex systems like fluid dynamics and heat transfer.

Applications in Differential Equations

One of the key applications of power series is in solving differential equations. By representing the solution as a power series, we can approximate the solution to the equation. This approach is particularly useful when the equation is nonlinear or has complex boundary conditions.

Approximating Functions via Power Series

Power series provide a powerful tool for approximating functions. By taking the first few terms of the series, we can obtain an approximation of the function that is accurate within a certain range. This technique is used in various fields, such as physics, engineering, and finance.

The applications of power series extend far beyond the theoretical realm, reaching into the practical world of calculus, science, and engineering. Their ability to represent functions as infinite sums of simpler terms makes them an essential tool for solving complex problems, developing approximation techniques, and gaining insights into intricate phenomena. As we delve deeper into the world of mathematics, the power of power series continues to astound and inspire.