Mastering Function Differentiability: Continuity, Difference Quotient, And Key Theorems

To know if a function is differentiable at a point, check continuity: is it continuous at that point? Calculate the difference quotient. If the difference quotient exists, verify the limit of the difference quotient: if it exists, the function is differentiable at that point. Differentiability implies continuity, but not vice versa. Rolle’s Theorem states that if a function is differentiable on an interval and has equal values at the endpoints, then there is a point in the interval where its derivative is zero. The Mean Value Theorem extends Rolle’s Theorem, ensuring that if a function is differentiable on an interval, there is a point in the interval where its derivative takes the average value of its rate of change over the interval.

Differentiability: A Measure of Smoothness and Rate of Change

In the realm of calculus, differentiability emerges as a crucial concept that unveils the smoothness and rate of change of functions. Differentiable functions possess a level of smoothness that allows for their precise analysis and application in various fields of science and engineering.

Significance in Calculus:

The concept of differentiability plays an integral role in calculus. It enables us to determine the derivative of a function, a powerful tool that measures the instantaneous rate of change. Derivatives unlock a wide array of applications, from calculating slopes of curves to optimizing functions.

Applications in Real-World Phenomena:

Beyond calculus, differentiability finds practical applications in numerous areas. In physics, it allows us to understand the motion of objects by calculating their velocity and acceleration. In economics, it helps economists predict market behavior by analyzing the rate of change in prices or demand.

Essential Concepts of Differentiability

Embarking on the journey of understanding differentiability, we encounter three fundamental concepts: the derivative, the difference quotient, and the limit. These pillars provide the foundation for our exploration of how functions behave as they change.

The derivative, a central notion in calculus, quantifies the instantaneous rate of change of a function. It measures how rapidly a function’s output responds to the slightest variation in its input. The difference quotient, a preliminary step in defining the derivative, calculates the average rate of change over a non-zero interval. As this interval shrinks to zero, the difference quotient converges to the derivative.

The limit plays a crucial role in defining both the derivative and differentiability. It describes the behavior of a function as its input approaches a specific value, even if the function is undefined at that point. The process of taking a limit involves examining the function’s behavior in an increasingly small neighborhood around the desired point.

Relationship to Differentiability

Differentiability is closely tied to these concepts. For a function to be differentiable at a point, the following must hold true:

• The function must be continuous at that point, meaning there are no abrupt jumps or breaks in its graph.
• The derivative of the function must exist at that point, indicating that the function’s graph has a definite slope at that point.

In essence, differentiability implies smoothness and a well-defined rate of change. Functions that are differentiable are often characterized by their curves that flow without sharp corners or discontinuities.

Differentiability and Continuity: An Intimate Yet Distinct Relationship

In the realm of calculus, differentiability and continuity are two interconnected concepts that play a pivotal role in understanding how functions behave. While differentiability implies continuity, the converse is not always true. This subtle distinction holds immense significance in the study of functions and their applications.

Differentiability measures the smoothness and rate of change of a function, quantified by the derivative. In essence, it indicates how rapidly the function’s output changes with respect to changes in its input.

Continuity, on the other hand, ensures that the function’s output undergoes no abrupt jumps or discontinuities as its input changes. In other words, a continuous function can be drawn without lifting the pen from the paper.

The Implication: Differentiability Ensures Continuity

Differentiability is a more stringent condition compared to continuity. If a function is differentiable at a given point, it must also be continuous at that point. This is because the process of differentiation involves taking a limit, which requires the continuity of the function at the point in question.

The Distinction: Continuity Does Not Imply Differentiability

However, the converse is not true. There exist functions that are continuous at a point but not differentiable at that point. This means that while the function may change smoothly at that point, its rate of change may not be defined.

Examples to Illustrate the Distinction

Consider the following examples:

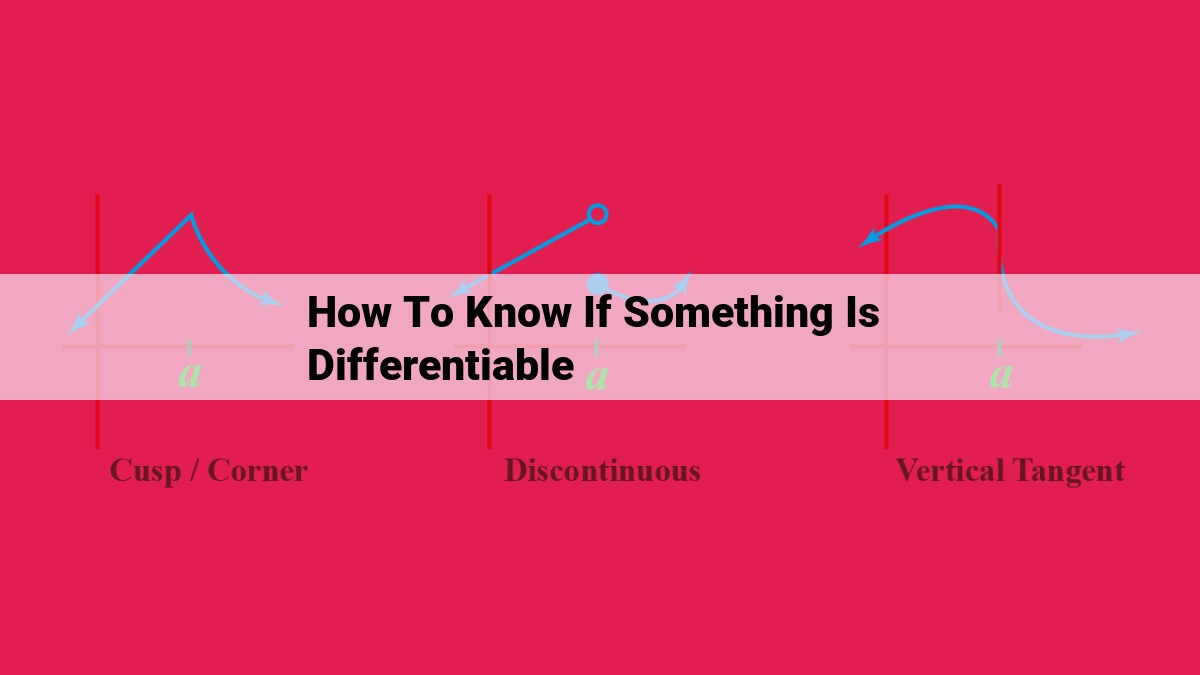
• The absolute value function, |x|: Continuous at x = 0 but not differentiable at x = 0. At this point, the function exhibits a sharp corner, resulting in an undefined derivative.
• The graph of a parabola: Continuous and differentiable everywhere. Its smooth, curved shape reflects the well-defined rate of change at each point.

These examples demonstrate that differentiability and continuity are two distinct concepts. While differentiability implies continuity, continuity alone does not guarantee differentiability. Understanding this distinction is crucial for a deeper appreciation of functions and their behavior.

Rolle’s Theorem and the Mean Value Theorem: Pivotal Tools in Differentiability

Rolle’s Theorem: Unveiling Differentiability

In the realm of calculus, differentiability serves as a cornerstone, measuring the smoothness and rate of change of a function. And at the heart of this concept lies Rolle’s Theorem, a pivotal tool that sheds light on the differentiability of functions.

According to Rolle’s Theorem, if a function f(x) satisfies the following conditions:

• Continuity: f(x) is continuous on the closed interval [a, b].
• Equal Values: f(a) = f(b).
• Differentiability: f(x) is differentiable on the open interval (a, b).

Then, there exists at least one point c in (a, b) such that the derivative of f(x) at c is equal to zero, i.e., f'(c) = 0.

Rolle’s Theorem’s Significance

This seemingly simple theorem holds immense significance in understanding differentiability. By establishing the existence of a point c where the derivative vanishes, Rolle’s Theorem reveals that functions that exhibit both continuity and equal values at endpoints must possess a constant rate of change over a subinterval. This crucial property is the hallmark of differentiability.

The Mean Value Theorem: A Generalization

Rolle’s Theorem serves as a precursor to the more general concept known as the Mean Value Theorem. This theorem extends Rolle’s findings by asserting that if a function f(x) satisfies the following:

• Continuity: f(x) is continuous on [a, b].
• Differentiability: f(x) is differentiable on (a, b).

Then, there exists at least one point c in (a, b) where the derivative of f(x), f'(c), equals the average rate of change of f(x) over [a, b]. This is mathematically expressed as:

f'(c) = (f(b) - f(a)) / (b - a)

Understanding the Mean Value Theorem

The Mean Value Theorem offers a powerful tool for analyzing functions by providing a way to relate the derivative to the average rate of change. For instance, if f(x) represents the position of an object at time x, then the derivative f'(x) represents its instantaneous velocity, while the average rate of change over [a, b] represents its average velocity. By equating these values at point c, the theorem asserts that there is an instant within the interval where the object’s instantaneous velocity matches its average velocity.

Rolle’s Theorem and the Mean Value Theorem stand as fundamental pillars in the study of differentiability. They establish a deep connection between continuity, derivatives, and average rates of change, helping us comprehend the critical role of differentiability in analyzing and understanding functions. These theorems serve as essential tools for mathematicians, scientists, and engineers alike, unlocking insights into the behavior of functions and their applications across various fields.

Determing Differentiability: A Step-by-Step Guide

In our journey to unravel the intricacies of differentiability, we now embark on a crucial step: determining whether a function exhibits this elusive smoothness at a particular point. Join us as we delve into a three-step process that will illuminate the path to understanding this fundamental concept.

Step 1: Seek Continuity

Before we can unravel the mysteries of differentiability, we must first establish a bedrock of continuity. A function must be continuous at the point in question to be considered differentiable there. Continuity ensures that the function’s graph has no abrupt jumps or breaks at that point, guaranteeing a seamless transition in its values.

Step 2: Embracing the Difference Quotient

With continuity as our foundation, we introduce the difference quotient, a powerful tool that quantifies the average rate of change between two points on the function’s graph. Formally, it is defined as:

(f(x) - f(a)) / (x - a)

where f(x) is the function, a is the point at which we’re assessing differentiability, and x is any other point in the function’s domain.

Step 3: Unveiling the Limit’s Secrets

Finally, we reach the culmination of our quest: evaluating the limit of the difference quotient as x approaches a. If this limit exists and is finite, then the function is differentiable at the point a. This limit represents the instantaneous rate of change at that point, providing a glimpse into the function’s behavior at its finest resolution.