Mastering Composite Figures: Calculating Area With Precision For Practical Applications

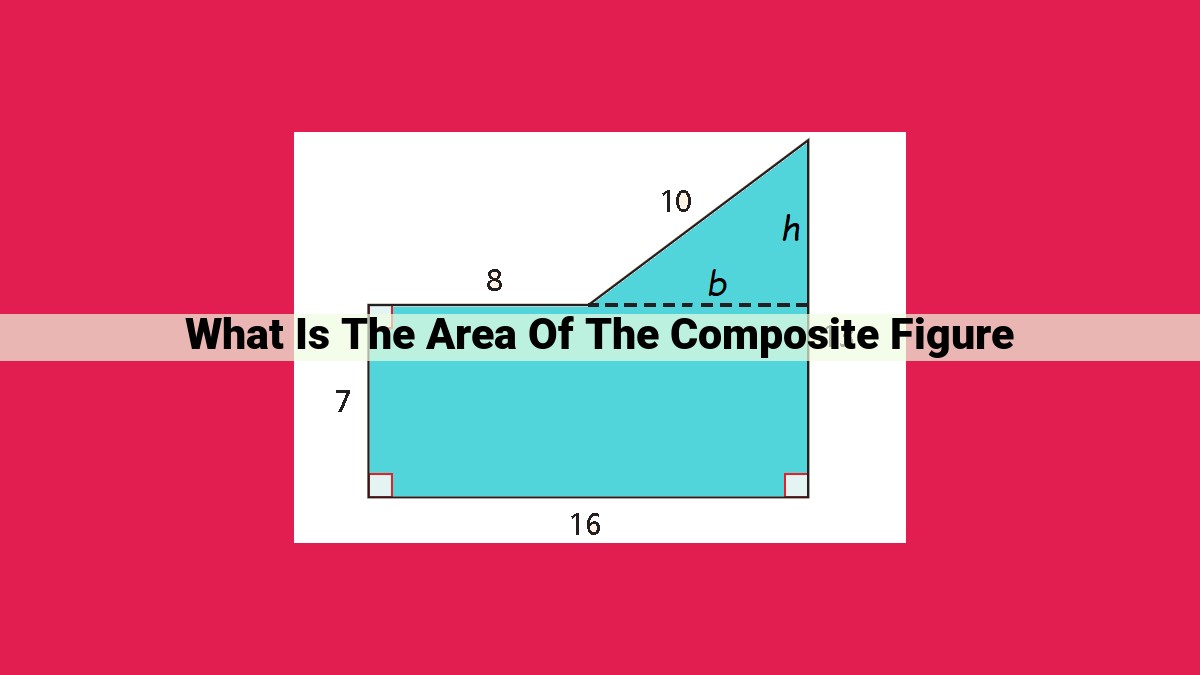
Composite figures are geometric shapes made up of smaller shapes. To find their area, we decompose them into individual shapes like rectangles and triangles. We calculate the area of each shape using formulas (e.g., area of rectangle = length × width, area of triangle = 1/2 × base × height) and then add the areas together. This allows us to determine the total area of the original composite figure, providing a crucial measurement for applications in architecture, engineering, and everyday life.

Understanding Composite Figures: A Beginner’s Guide to Shape Complexity

In the realm of geometry, composite figures take center stage as intriguing puzzles that challenge our understanding of space and shapes. These captivating creations are formed by combining two or more basic shapes, such as triangles, rectangles, or circles, to create a more complex and visually striking entity. From intricate works of art to everyday objects, composite figures are everywhere around us.

Decoding the Definition

A composite figure is a masterfully composed shape that seamlessly integrates multiple simpler shapes into a cohesive whole. Each individual shape within the composite figure maintains its distinct identity while contributing to the overall form and function of the larger structure.

Examples of Composite Figures in Our World

In the vast tapestry of our world, composite figures weave their way into countless objects and designs. The facade of a majestic building, adorned with arched windows and triangular gables, showcases the captivating beauty of composite figures in architecture. Similarly, the intricate patterns on a mosaic floor, meticulously assembled from smaller tiles, demonstrate the artistic allure of these geometric creations.

Calculating Area of Composite Figures

Understanding the Concept of Area

In geometry, the area of a figure represents the amount of two-dimensional space it occupies. For composite figures, which are made up of multiple smaller shapes, calculating the total area can be a bit more challenging.

Steps to Determine the Area of a Composite Figure

1. Identify the individual shapes: Composite figures can be composed of rectangles, triangles, circles, and other geometric shapes. The first step is to identify each individual shape.

2. Decompose the figure: Once the individual shapes have been identified, decompose the composite figure by breaking it down into its component parts.

3. Calculate the area of each shape: Use the appropriate area formula for each shape. For example, for rectangles, the area is length x width; for triangles, it’s 1/2 x base x height.

4. Add the areas together: Finally, add the areas of the individual shapes to get the total area of the composite figure.

Example: Calculating the Area of a Rectangle-Triangle Composite

Consider a composite figure made up of a rectangle with a length of 5 units and a width of 3 units, and a right triangle with a base of 4 units and a height of 3 units.

To calculate the total area, first, find the area of the rectangle: 5 units x 3 units = 15 square units.

Next, find the area of the triangle: 1/2 x 4 units x 3 units = 6 square units.

Finally, add the areas of the rectangle and triangle: 15 square units + 6 square units = 21 square units.

Therefore, the total area of the rectangle-triangle composite figure is 21 square units.

Common Composite Figures and Their Areas

Composite figures are complex shapes that are composed of two or more simple shapes, such as rectangles, triangles, and circles. Understanding how to calculate the area of these figures is essential for various applications, including architecture, construction, and engineering.

One of the most common composite figures is a rectangle, which is a four-sided figure with opposite sides parallel. The area of a rectangle is calculated by multiplying the length by the width (length × width). For instance, if a rectangle has a length of 5 units and a width of 3 units, its area would be 5 × 3 = 15 square units.

Another common composite figure is a triangle. This three-sided figure has a base and a height. The area of a triangle is calculated by multiplying the base by the height and dividing the result by two (1/2 × base × height). For example, if a triangle has a base of 4 units and a height of 6 units, its area would be 1/2 × 4 × 6 = 12 square units.

Understanding the formulas for rectangles and triangles will enable you to calculate the area of various composite figures. By decomposing the composite figure into its individual shapes, calculating the area of each shape, and then adding them together, you can determine the total area of the complex shape.

Decomposing Composite Figures: Unraveling the Puzzle of Complex Shapes

In the realm of geometry, composite figures emerge as complex shapes that challenge our ability to calculate their area. These polygonal puzzles are composed of simpler individual shapes, each with its unique characteristics. To conquer these geometric enigmas, we embark on a journey of decomposition and calculation.

Imagine a composite figure resembling a house. Its walls are rectangles, its roof a triangle, and its chimney a cylinder. By decomposing this figure, we break it down into its constituent parts: rectangles, a triangle, and a cylinder.

With each piece identified, we calculate their individual areas using the appropriate formulas. For rectangles, we multiply their length and width. For triangles, we employ the formula (1/2) x base x height. And for cylinders, we utilize the equation 2πr² + 2πrh, where r represents the radius and h the height.

Similarly, any composite figure can be dismantled into individual shapes. Each shape’s area is meticulously calculated, contributing to the total puzzle’s solution. By summing the areas of these individual components, we assemble the complete picture and determine the total area of the composite figure.

Putting It All Together: Calculating the Total Area of Composite Figures

Understanding Composite Figures

Composite figures are geometric shapes that are made up of two or more smaller shapes. To calculate the area of a composite figure, you need to decompose it into its individual shapes and then calculate the area of each shape. Once you have the area of each shape, you can add them together to get the total area of the composite figure.

Common Composite Figures

Some of the most common composite figures include rectangles, triangles, and circles. The formulas for calculating the area of these shapes are:

• Rectangle: Area = length × width
• Triangle: Area = 1/2 × base × height
• Circle: Area = π × radius²

Decomposing and Calculating

To decompose a composite figure, you need to identify the different shapes that make it up. Once you have identified the shapes, you can use the formulas above to calculate the area of each shape.

For example, let’s say you have a composite figure that is made up of a rectangle and a triangle. To calculate the area of the composite figure, you would first calculate the area of the rectangle using the formula Area = length × width. Then, you would calculate the area of the triangle using the formula Area = 1/2 × base × height. Finally, you would add the areas of the rectangle and the triangle together to get the total area of the composite figure.

Putting It All Together

Once you have calculated the area of each individual shape, you can add them together to get the total area of the composite figure. The total area of the composite figure is equal to the ****sum of the areas of its individual shapes****.

For example, if the rectangle in the example above has a length of 5 cm and a width of 3 cm, and the triangle has a base of 4 cm and a height of 3 cm, then the total area of the composite figure would be:

Area of rectangle = 5 cm × 3 cm = 15 cm²
Area of triangle = 1/2 × 4 cm × 3 cm = 6 cm²
Total area = 15 cm² + 6 cm² = 21 cm²

Calculating the area of composite figures can be a bit tricky, but it is a skill that is essential for anyone who works with geometry. By following the steps outlined in this post, you can learn how to decompose composite figures, calculate the area of each individual shape, and add them together to get the total area of the composite figure.

Additional Considerations for Area Calculations of Composite Figures:

When dealing with composite figures, understanding some essential concepts is crucial for accurate area calculations. Let’s delve deeper into base, height, length, and width:

• Base: This is typically the bottom or lower part of a figure upon which it rests. It’s a horizontal measurement. For instance, in a rectangle, the base is the horizontal side.

• Height: This is the vertical measurement of a figure from its base to its top. In a rectangle, the height is the vertical side.

• Length: This refers to the horizontal measure of a figure from one end to the other. In a rectangle, the length is the longer horizontal side.

• Width: This is the horizontal measurement of a figure from one side to the other. In a rectangle, the width is the shorter horizontal side.

Remember, these concepts are key in determining the area of various shapes and, consequently, composite figures. By understanding these terms and their relationship to area calculations, you’ll be well-equipped to tackle any composite figure with confidence.