Master Trapezium Area Calculation: An In-Depth Guide
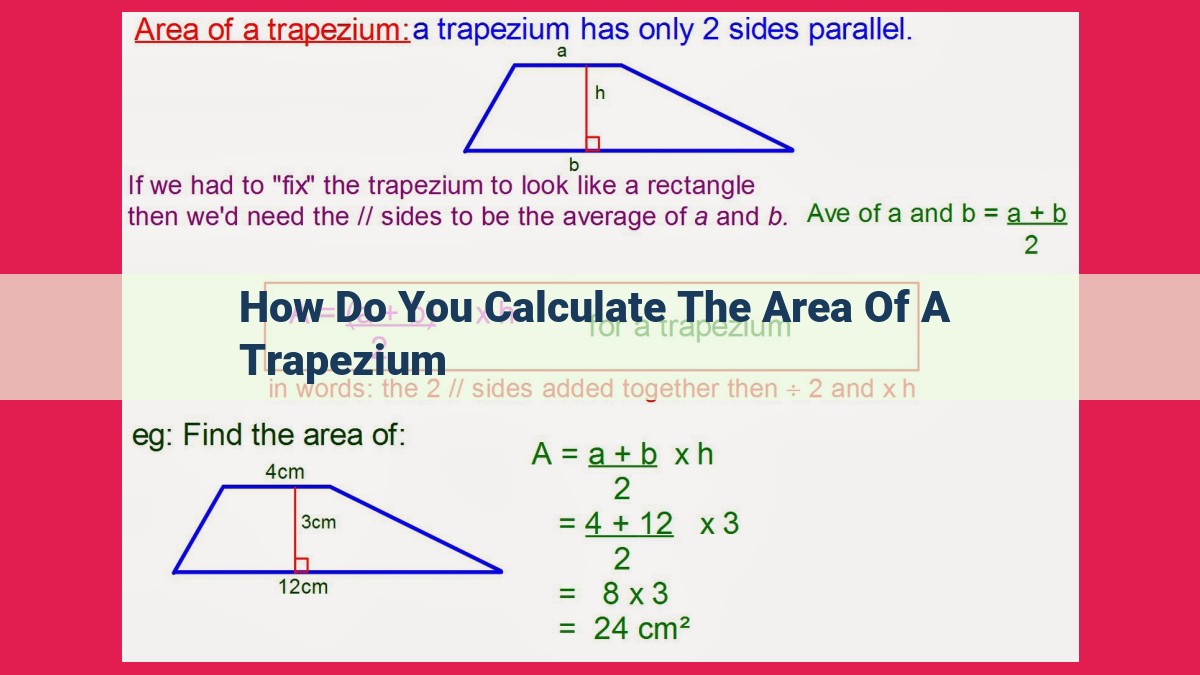
To calculate the area of a trapezium, determine its two parallel bases and the height (the perpendicular distance between the bases). The area formula is: Area = (1/2) x (Base 1 + Base 2) x Height. Sum the lengths of the bases and multiply the result by half to obtain half of the sum. Next, multiply this value by the height to get the trapezium’s area. This formula differs from that of other shapes, highlighting the unique area determination method for trapeziums.
In the realm of geometry, where shapes dance and patterns emerge, the trapezium stands as a captivating figure. Trapeziums are quadrilaterals—four-sided shapes—with a unique characteristic: two parallel sides, known as bases. The other two sides, called legs, are non-parallel and often sloped.
Trapeziums share a kinship with other quadrilaterals. They are cousins of parallelograms, which also have two parallel sides, and rhombuses, which boast equal sides and parallel sides. However, what sets trapeziums apart is that their non-parallel sides distinguish them from their more symmetrical counterparts.
This intriguing shape holds a special place in the study of geometry, not only for its distinctive features but also for its role in understanding the measurement of area. In the chapters that follow, we will delve into the intricacies of trapeziums, examining their characteristics, exploring their relationship with other quadrilaterals, and uncovering the secrets of calculating their area.
Area of Trapeziums: Unveiling a Key Concept
In the realm of geometry, understanding the area of trapeziums holds immense significance. Area represents the extent of a two-dimensional surface, providing a quantitative measure of the space it occupies. For trapeziums, this measurement becomes crucial in various applications involving shapes and dimensions.
Trapeziums, a unique class of quadrilaterals, possess two parallel sides, known as bases. Unlike rectangles or parallelograms, trapeziums have non-parallel sides, giving them a distinct shape. The area of a trapezium serves as a crucial aspect in determining its size and spatial characteristics.
When comparing area of trapeziums with other shapes, it’s essential to acknowledge the similarities and differences. Triangles and rectangles, possessing a single base, employ a straightforward formula involving half the base and height. Parallelograms, on the other hand, share the same parallel sides as trapeziums but differ in their opposite sides being congruent. Their area formula mirrors the product of base and height.
Understanding the area of trapeziums not only provides geometric knowledge but also lays the foundation for solving practical problems in fields like architecture, engineering, and design. By grasping the concept of area, we equip ourselves with a valuable tool for quantifying spatial relationships, enabling us to make informed decisions involving shapes and dimensions.
Dissecting Trapezium Bases
- Definition and purpose of trapezium bases
- Distinction from other quadrilateral sides
Dissecting Trapezium Bases: Unraveling the Foundations
In the realm of geometry, where shapes dance and dimensions collide, we explore the enigmatic trapezium. This unique quadrilateral, characterized by its parallel bases, holds a special place in our mathematical adventures. But what exactly are these bases, and how do they distinguish the trapezium from its quadrilateral brethren?
Imagine a trapezium as a house with two elongated walls, the bases, running parallel to each other like trusty foundations. These bases are the pillars upon which the trapezium’s structure rests, defining its shape and setting it apart from other quadrilaterals. Unlike rectangles, where all sides are parallel, or parallelograms, where only the opposite sides are parallel, the trapezium’s bases stand proudly parallel, giving it a distinct trapezoidal silhouette.
The distinction between trapezium bases and other quadrilateral sides is crucial. While rectangles and squares possess four equal sides, the trapezium’s bases vary in length, creating unique and versatile shapes. This difference allows trapeziums to mold themselves into various forms, from right trapeziums with one right angle to isosceles trapeziums with congruent bases, each with its own geometric charm.
So, next time you encounter a trapezium, take a moment to admire its gracefully parallel bases. They are not mere sides, but the defining characteristics that set this intriguing shape apart, paving the way for a world of geometric possibilities.
The Height of Trapeziums: Measuring Vertically
In the realm of geometry, understanding the nuances of various shapes is essential. Among these, trapeziums stand out with their unique combination of parallel and non-parallel sides. One crucial aspect of analyzing trapeziums is determining their height. This vertical measurement plays a pivotal role in calculating their area.
The height of a trapezium is the perpendicular distance between its two parallel bases. To visualize it, imagine a ladder leaning against a wall. The vertical distance from the ground to the top of the ladder is analogous to the height of the trapezium.
Unlike rectangles or parallelograms, trapeziums can have different lengths for their bases. Therefore, the height of a trapezium is the average of the two parallel base lengths.
Trapezium height is closely related to the height of other shapes. In a triangle, for instance, the height is the perpendicular distance from a vertex to the opposite side. Similarly, in a parallelogram, the height is the distance between parallel sides.
Understanding trapezium height is crucial for calculating its area. The area of a trapezium is half the product of its height and the sum of its bases. This formula highlights the importance of accurately measuring the height to determine the trapezium’s area precisely.
Unveiling the Formula for Trapezium Area
Trapeziums, those distinctive quadrilaterals with their parallel bases, possess a unique formula that unlocks the secret to their area. Let’s embark on a step-by-step journey to uncover this enigmatic formula.
Step 1: Visualizing the Trapezium
Imagine a trapezium spread out before you. Its parallel bases, like railway tracks, stretch out before your eyes. The two non-parallel sides, like sloping hills, connect the bases.
Step 2: Dividing into Triangles
Now, let’s visualize a diagonal line slicing through the trapezium, dividing it into two triangles. These triangles, like identical twins, share the same height, which is the perpendicular distance between the bases.
Step 3: Area of Triangles
The area of each triangle is calculated using the familiar formula: Area = ½ x base x height. Since the trapezium’s bases and height are also the bases and heights of these triangles, we can see that the total area of the trapezium is simply the sum of the areas of the two triangles: Area = ½ x (base1 + base2) x height.
Step 4: Comparison with Other Shapes
This formula bears striking similarities to other quadrilateral shapes. For instance, when the bases become equal in length, the trapezium transforms into a parallelogram, and the formula simplifies to the parallelogram’s area: Area = base x height. Similarly, when the height shrinks to zero, the trapezium becomes a degenerate triangle, and the formula reduces to the familiar Area = ½ x base x height.
The formula for the area of a trapezium, Area = ½ x (base1 + base2) x height, is a testament to the interconnectedness of geometry. Its derivation, a masterpiece of mathematical ingenuity, reveals the hidden relationships that govern the world of shapes.
Measuring Area Units: Quantifying Trapezium’s Spatial Dimensions
As we dive deeper into the realm of trapeziums, it’s essential to understand the units we use to quantify these geometric shapes’ area. These units serve as the language we use to measure the extent of their two-dimensional expanse.
Commonly, area is expressed in square units, such as square centimeters (cm²) or square meters (m²). Think of these units as tiny squares that, when arranged side-by-side, cover the surface of a trapezium. By counting how many of these squares it takes to fill the trapezium, we can determine its area.
The relationship between these area units and the dimensions of a trapezium is crucial in calculating its size accurately. The area formula for a trapezium, A = (1/2) * (b1 + b2) * h, relies on two bases (b1 and b2) and a height (h). Understanding how these units interact with each other enables us to precisely determine the surface area of the trapezium.
By choosing appropriate units that align with the scale of the trapezium, we can efficiently express its area. For instance, if the trapezium is relatively small, centimeters might be a suitable unit. However, if it’s significantly larger, meters would provide a more precise representation.
Mastering the concept of area units empowers us to communicate the size of trapeziums effectively. Whether we’re collaborating on architectural plans or describing real-world objects, these units act as a standardized language that allows clear and accurate understanding between individuals.