Master Solution Sets Writing For Equations: An Ultimate Guide

How to Write Solution Sets:

1. Introduction: Define solution sets and their types (algebraic, graphical, exact, approximate)
2. Methods: Explain algebraic, graphical, numerical, and exact solution methods for equations.
3. Representation: Describe how to write general, particular, approximate, and parametric solutions using variables, decimal approximations, or inequalities.
4. Significance: Emphasize the importance of choosing the appropriate solution method based on the problem type and desired precision.

• Define solution sets and their significance
• Introduce different types of solution sets (e.g., algebraic, graphical, exact, approximate)

What is a Solution Set and Why is it Important?

In the realm of mathematics, we encounter countless equations and problems that require us to find solutions. A solution set represents the collection of all solutions that satisfy those equations or problems. It plays a crucial role in understanding the behavior of mathematical functions and solving real-world scenarios. By identifying the solution set, we gain insights into the possible outcomes and restrictions associated with a given equation or problem.

Types of Solution Sets

Solution sets can be classified into various types, each with its unique characteristics:

• Algebraic Solutions: Obtained by solving equations using algebraic methods, these solutions provide exact values or general expressions involving variables.
• Graphical Solutions: Found by plotting equations on a graph and identifying the points of intersection. Graphical solutions offer approximate solutions but can visualize the relationship between variables.
• Exact Solutions: Represent the precise values that satisfy an equation. They can be found using algebraic or graphical methods but require certain conditions to be met.
• Approximate Solutions: Estimated values that closely represent true solutions but may not be exact due to limitations in calculation methods or the nature of the equation.

Understanding the different types of solution sets allows us to choose the most appropriate method for solving equations and problems based on the precision required and the available information.

Algebraic Solutions to Equations: A Step-by-Step Guide

In the realm of Mathematics, equations hold a prominent place. They allow us to describe relationships between variables and delve into the intricacies of the world around us. Algebraic solutions are a fundamental tool for solving these equations, empowering us to uncover the elusive values that satisfy them.

Finding Algebraic Solutions

The art of finding algebraic solutions lies in the skillful manipulation of equations. By employing algebraic operations such as addition, subtraction, multiplication, and division, we can isolate the variable on one side of the equation, revealing its true value. This process is analogous to a detective unraveling a mystery, using logic and precision to uncover the truth.

General and Particular Solutions

When seeking algebraic solutions, we encounter two distinct types: general and particular. General solutions, represented by variables, offer a broad view of all possible values that satisfy the equation. Particular solutions, on the other hand, are specific numerical values that meet the equation’s conditions. The relationship between these two types of solutions is akin to a family tree: general solutions represent the ancestors, while particular solutions are their descendants.

Graphical Solutions: Unlocking Visual Pathways to Math Success

In the realm of mathematics, graphical solutions emerge as a powerful tool, offering a visual representation of equations that simplifies the process of finding solutions. This approach transcends the complexities of algebra and numerical methods, providing an intuitive understanding of problem-solving.

To embark on this graphical journey, the first step involves transforming the equation into a coordinate plane. By plotting the equation’s points and connecting them, we form a graph, revealing the relationship between the variables. This visual representation empowers us to estimate approximate solutions by identifying points where the graph intersects the x-axis or y-axis.

However, it’s important to acknowledge that graphical solutions are not exact. They provide estimations rather than precise values. Yet, this approximation can be extremely useful when accuracy is not a paramount concern or when dealing with complex equations where exact solutions are difficult to obtain.

Consider a scenario where we need to find the solutions to the equation y = x^2 – 2. By graphing this equation, we obtain a parabola. The points where this parabola intersects the x-axis give us the approximate solutions to the equation. Although these solutions may not be exact, they provide a valuable insight into the relationship between x and y.

In conclusion, graphical solutions serve as a versatile tool for problem-solving, offering a visual interpretation of equations and enabling us to estimate approximate solutions. While they may not yield exact results, their simplicity and intuitive nature make them an invaluable asset for a diverse range of mathematical applications.

Numerical Solutions for Approximate Answers

In the realm of mathematics, exact solutions can be elusive, especially when equations become intricate. Numerical solutions offer a practical alternative, providing approximate answers that can be invaluable for real-world applications.

Numerical methods, such as iteration and bisection, are designed to hone in on approximate solutions iteratively. These methods work by estimating a solution and then refining that estimate until a satisfactory level of accuracy is achieved.

Iteration involves repeatedly substituting a value into an equation, using the result of each iteration as the input for the next. This process continues until the difference between successive iterations becomes negligible.

Bisection is another powerful method that divides an interval containing the solution in half repeatedly. By identifying which half contains the solution, the interval is narrowed down with each iteration, leading to an increasingly accurate approximation.

Numerical solutions are particularly useful when exact solutions are impractical or infeasible. For example, in engineering, approximating the solution to a complex differential equation can be crucial for designing efficient systems.

However, it’s important to be aware of the limitations of numerical solutions. They can be computationally intensive, especially for high-dimensional problems. Additionally, the accuracy of numerical solutions is dependent on the number of iterations or the choice of initial interval.

Despite these limitations, numerical solutions remain an indispensable tool for solving complex equations that arise across various fields of science, engineering, and economics. By providing approximate answers, they enable us to gain valuable insights into real-world phenomena and make informed decisions based on practically useful solutions.

Exact Solutions: Pinpoint Precision in Mathematics

In the realm of mathematics, exact solutions are the holy grail of problem-solving. Unlike approximate solutions, which hover around the correct answer, exact solutions hit the nail on the head with unwavering accuracy.

Identifying Exact Solutions:

Identifying exact solutions is akin to spotting a diamond amidst a pile of pebbles. Look for algebraic expressions that can be simplified to a single value, without any variables or unknown quantities remaining. For instance, the expression 2 + 3 has an exact solution of 5.

Verifying Exact Solutions:

Once you’ve spotted a potential exact solution, don’t take its word for it. Verify it using one of two methods:

• Substitution: Plug the solution into the original equation and see if it holds true. For instance, if your solution is x = 5, substitute it into the equation x + 2 = 7. It does indeed equal 7, confirming the exactness of the solution.

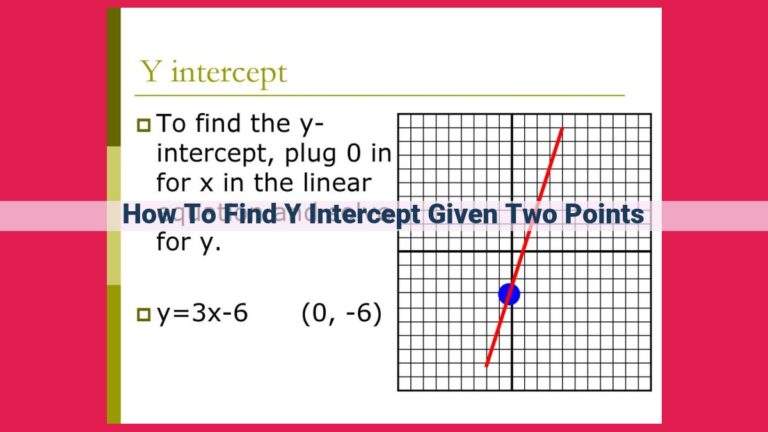
• Graphing: Graph the equation and locate the point where it crosses the x-axis or y-axis. The coordinates of this point correspond to the exact solution. For example, the equation y = 2x + 1 graphs as a straight line. The point where it crosses the y-axis is (0, 1), which is the exact solution for y.

Value and Significance:

Exact solutions are not just a mathematical nicety; they hold immense value in practical applications. From engineering calculations to financial planning, precise solutions ensure reliable outcomes. They eliminate uncertainties and provide a solid foundation for decision-making.

Exact solutions are the ultimate goal for any problem-solver. By understanding how to identify and verify them, you can unlock the power of precise mathematics and solve problems with an unmatched level of accuracy. So, next time you embark on a mathematical journey, strive for exact solutions and revel in the satisfaction of knowing that your answer is definitively correct.

Approximating Solutions: Unveiling the Secrets of Decimal Delights and Inequality Escapades

Sometimes, the world of algebra presents us with equations that don’t yield exact solutions. But fear not, dear reader, for we have a magical tool called approximation to guide us through the mathematical labyrinth.

Decimal Delights

An approximate solution, expressed as a decimal approximation, is a value that gets us pretty darn close to the actual solution. We simply convert our fractional solution into a decimal by dividing the numerator by the denominator. For instance, if our solution is 13/6, our decimal approximation is approximately 2.167.

Inequality Escapades

When a decimal approximation isn’t precise enough, we can use inequalities to define our solution’s range. For example, if our decimal approximation is 2.167, we can say that our solution is between 2.1 and 2.2 (2.1 < solution < 2.2). This gives us a bit more breathing room while still keeping us within the ballpark of the actual answer.

Accuracy and Significance: A Balancing Act

It’s important to know that approximate solutions have an accuracy and a significance. Accuracy refers to the number of decimal places in our approximation, while significance tells us how many of those decimal places are meaningful. For example, if our approximate solution is 2.166666… and our significance is 4, then the first four decimal places (2.1666) are considered significant.

Choosing the Right Approximation Method

The method we use to approximate a solution depends on the problem and the desired level of precision. If a quick estimate is all we need, a decimal approximation will suffice. However, if we need a more precise answer, an inequality might be a better choice.

Approximating solutions is a valuable skill in the mathematical explorer’s toolkit. It allows us to navigate through equations that might not have exact solutions, giving us insights into the complex world of numbers. Whether it’s decimal approximations or inequality escapades, remember that the journey of approximation is a quest for knowledge that unlocks the secrets of the mathematical realm.

General Solutions: A Guiding Light in the Equation Labyrinth

When venturing into the world of equations, the concept of solution sets serves as a compass, directing us towards the “treasures” hidden within mathematical expressions. One type of solution set that stands out is the general solution. It’s like a master key, unlocking a wide range of possible values that can satisfy an equation.

General solutions are represented using variables, often denoted by letters such as x, y, or z. These variables act as placeholders, allowing us to represent an entire family of solutions. For instance, the equation x + y = 5 has a general solution of (x, y), where x and y can take any values that sum up to 5. This solution set encompasses an infinite number of possibilities, making it a powerful tool for understanding the behavior of equations.

General solutions are particularly useful when dealing with families of curves. Consider the equation y = mx + b, which represents a straight line. The general solution for this equation is (x, mx + b). As we vary the parameters m and b, we generate different lines that all satisfy the original equation. This demonstrates the versatility of general solutions in describing a wide range of curves or surfaces.

Differentiating general solutions from particular solutions is crucial. Particular solutions represent specific points or values that satisfy an equation under certain conditions. For example, if we are given the equation x + y = 5 and told that y = 2, then the particular solution is (3, 2). This solution is unique, unlike the general solution, which encompasses an infinite number of possibilities.

Mastering the art of finding general solutions is a fundamental step in the equation-solving journey. It empowers us to understand the underlying principles that govern mathematical relationships and opens the door to a vast array of problem-solving techniques.

Particular Solutions: Tailoring Solutions to Specific Needs

In the realm of problem-solving, solution sets offer a multitude of answers. Among these varied solutions, particular solutions stand out as tailored responses that fulfill certain conditions or values.

To derive a particular solution, specific conditions are applied to a general solution. Think of it as applying a filter to a broader set of possibilities. This process narrows down the options, ultimately yielding a solution that precisely meets the given requirements.

Particular solutions are particularly valuable when dealing with equations involving **parameters__. These __parameters__ represent unknown values that can be customized to satisfy specific scenarios. By plugging in these values, we can **generate__ particular solutions that are precisely calibrated for our unique needs.

Connecting particular solutions to other methods, such as algebraic and graphical, provides a versatile toolkit for problem-solving. Just as a sculptor uses different tools to refine a masterpiece, mathematicians employ various techniques to find the most appropriate solution for each situation.

Particular solutions offer a direct path to answers that align with specific criteria. They are like precision instruments, meticulously crafted to meet the demands of each unique mathematical challenge.

Parametric Solutions: Unveiling a Flexible Approach to Problem-Solving

In the realm of mathematics, solution sets play a pivotal role in deciphering equations and finding their corresponding answers. Among these solution sets, parametric solutions stand out as a versatile tool that offers a unique perspective on problem-solving.

Parametric solutions are expressions of solutions that incorporate parameters, which are variables that can assume any value within a specified range. By introducing parameters, we gain the flexibility to represent a family of solutions rather than a single fixed solution.

Imagine a scenario where you need to find the solution to the equation y = mx + b. Using algebraic techniques, you might determine that the solution is a straight line with slope m and y-intercept b. However, what if you want to explore different lines that satisfy this equation?

That’s where parametric solutions come in. By introducing a parameter t, you can express the solution as x = at + c and y = bt + d, where (a, b) represents the slope and (c, d) represents the y-intercept. By varying the value of t, you can generate an infinite number of lines that all satisfy the original equation.

This parametric representation grants you immense power. You can visualize the family of lines in a graph, where each line represents a specific value of t. This graphical representation provides valuable insights into the behavior of the equation and allows you to explore different scenarios easily.

Moreover, parametric solutions have a close connection to general solutions. A general solution is an expression that represents all possible solutions to an equation, without specifying any particular values for the variables. Parametric solutions can be viewed as particular solutions that are obtained by assigning specific values to the parameters.

In essence, parametric solutions offer a dynamic and flexible way to explore and visualize solution sets. They allow you to represent a range of solutions, understand how they relate to each other, and gain a deeper comprehension of the underlying equation.

So, next time you encounter a problem that calls for a solution set, consider the power of parametric solutions. By embracing this approach, you’ll unlock a world of mathematical possibilities and gain a newfound appreciation for the beauty and versatility of algebraic expressions.