Master Parametric Equation Graphing On Desmos: Unlocking Customization And Storytelling
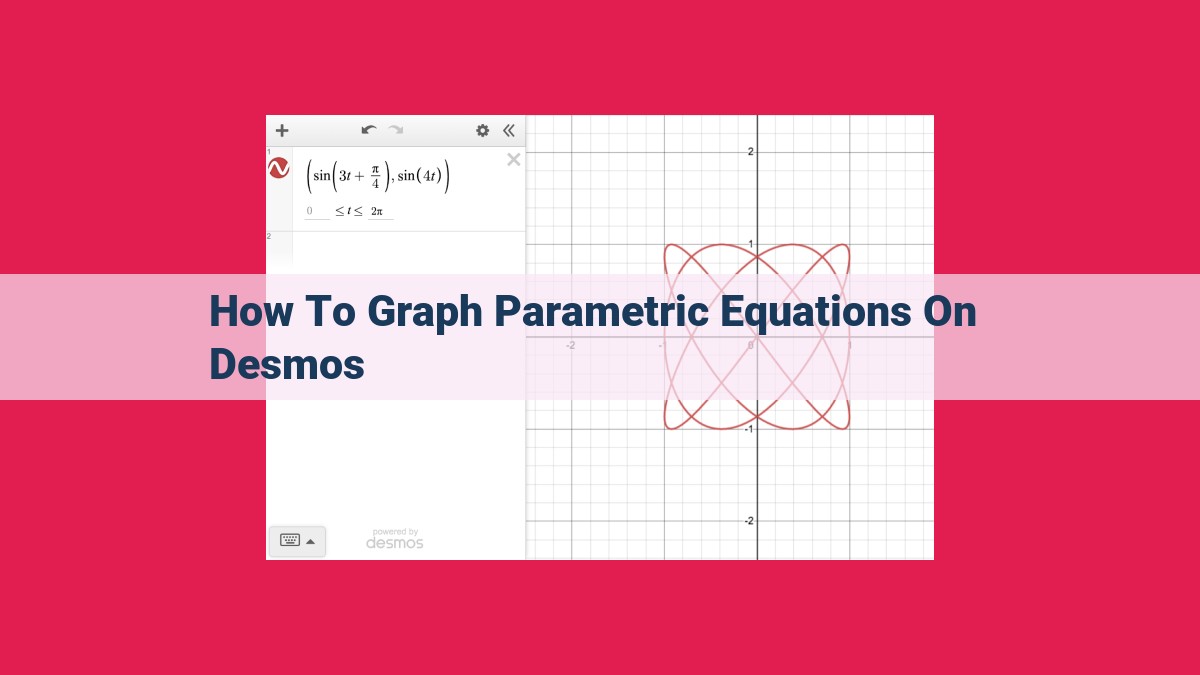
To graph parametric equations on Desmos, input the equations in the form x = f(t) and y = g(t). Customize parameters to control animation range and duration. Enhance the graph’s aesthetics with colors, gridlines, and trace options. Integrate sliders for interactive input. Export and share graphs to communicate findings.
Understanding Parametric Equations
- Definition and graphical representation of parametric equations
- Describing coordinates, functions, and how they relate to graphing
Understanding Parametric Equations: A Geometric Adventure
In the vast realm of mathematics, parametric equations ignite a spark of elegance that defies the confines of standard Cartesian coordinates. These enigmatic equations unlock the secrets of curves and surfaces, revealing their beauty in a new and captivating light.
Parametric equations breathe life into geometric shapes by introducing a time parameter, t, which functions as a conductor guiding the dance of coordinates. Each value of t orchestrates a distinct point on the curve, creating a dynamic and ever-evolving tapestry of geometric patterns.
At its core, a parametric equation comprises a set of equations, one for each Cartesian coordinate (x and y). These equations are functions of the parameter t, the maestro of the geometric ballet. By manipulating these functions, we paint the canvas of the coordinate plane with an infinite array of curves, each possessing its own unique character and flair.
Delving deeper into the intricacies of parametric equations, we discover that the functions for x and y serve as blueprints for the curve’s path. The x function defines the horizontal movement, while the y function governs the vertical ascent and descent. As t marches onward, the coordinates x and y dance in harmony, tracing out the contours of the curve.
Through this dance of coordinates, parametric equations unveil the profound relationship between algebra and geometry. By manipulating equations, we not only command the motion of points but also craft intricate shapes that ignite our imagination and challenge our preconceived notions of geometric form.
Using Desmos to Unleash the Power of Parametric Equations
Embark on a graphical adventure with parametric equations! Using the user-friendly Desmos platform, you can effortlessly input these equations and unlock a world of visual animations. Its intuitive interface empowers you to create stunning graphs with ease.
Step-by-Step Input
- Navigate to Desmos and click on the Custom Equation tab.
- Select the Parametric Equations option.
- Enter your equations in the “x(t)” and “y(t)” fields using the variable “t” as the parameter.
Customizing Parameters
Delve into the realm of customization to personalize your graphs to perfection. Desmos allows you to adjust:
- Parameter Range: Control the animation’s visible range by setting the minimum and maximum values of “t.”
- Animation Duration: Speed up or slow down the animation by changing the time it takes for “t” to vary from the minimum to maximum values.
- Trace Enabled: Turn on the trace to leave a trail behind the moving point, enhancing visualization.
Additional Tips
- Explore the Graph Settings menu to customize gridlines, colors, and more.
- Test different parameter ranges to visualize the equation’s behavior.
- Experiment with different equations to discover the diverse range of possible graphs.
Customizing Graph Properties: Tailoring Parametric Animations to Perfection
In the realm of parametric equations, where graphs dance to the rhythm of parameters, the ability to customize these properties unlocks a world of possibilities. By adjusting parameter ranges, you can control the animation’s flow, manipulating its speed and smoothness for an optimal visual experience.
Fine-tuning the Parameter Range: Shaping the Animation’s Dance
The parameter range serves as a choreographer for your animated graph, guiding its movement within the Cartesian plane. By adjusting the starting and ending values, you can determine the extent of the graph’s traversal. A wider range allows for a more expansive performance, while a narrower range confines the animation to a specific region of the plane.
Orchestrating Animation Duration: Setting the Pace of the Dance
The animation duration is the timekeeper of your parametric ballet, determining the speed at which the graph evolves. A longer duration allows the animation to unfold gracefully, allowing viewers to appreciate its nuances. Conversely, a shorter duration accelerates the dance, creating a more dynamic and captivating effect.
Illuminating the Trace: Unveiling the Path Behind the Scenes
The trace option provides a visual record of the graph’s journey as it animated. By enabling the trace, you can unveil the path traced by the graph, gaining insights into its trajectory and motion. This feature is particularly useful for understanding the underlying mechanics of the parametric equation.
Enhancing Graph Aesthetics: The Art of Visualizing Data
Parametric equations, with their ability to represent curves and surfaces dynamically, offer a powerful tool for data visualization. To effectively convey information and engage readers, it’s crucial to consider the aesthetics and design of your graphs.
Selecting Colors, Styles, and Gridlines
The choice of colors, styles, and gridlines can significantly impact the readability and aesthetics of your graph. Vibrant colors can draw attention to important features, while contrasting colors can enhance the visibility of different curves. Dashed lines or dotted lines can distinguish between multiple datasets, while thicker lines can emphasize specific sections of the graph.
Importance of Aesthetics in Effective Graphing
A visually appealing graph not only enhances its aesthetic value but also facilitates data interpretation. Clear labels and consistent units ensure that readers can easily understand the graph’s axes and scales. Gridlines provide a reference grid for accurate measurements and comparisons. By carefully considering aesthetics, you can create graphs that effectively convey information and make a lasting impression.
Customizing Graph Properties for Optimal Visualization
In addition to selecting colors and styles, you can customize other graph properties to optimize its visual impact. Adjusting the parameter range allows you to control the animation speed, creating graphs that are either fluid or deliberate. Manipulating the animation duration ensures that the graph plays smoothly, enhancing its visual appeal. Enabling the trace option allows readers to trace the path of the animation, providing a more dynamic visualization experience.
Interactive Features: Enhancing User Experience with Sliders
Parametric equations bring graphs to life by introducing animation, and to enhance this experience even further, we can use Desmos’ interactive features.
One such feature is the integration of sliders. Sliders allow users to interact with the graph in real-time, providing control over the animation. By adjusting the slider’s value, users can modify the parameters of the equations, altering the shape, motion, and appearance of the graph.
This interactivity not only enhances the user experience but also serves as an effective teaching tool. Users can manipulate the parameters and observe the corresponding changes in the graph, gaining a deeper understanding of the relationship between the equations and the resulting animation.
For instance, let’s consider a parametric equation describing a circle:
x = r * cos(t)
y = r * sin(t)
By adding a slider to control the parameter t, users can rotate the circle, changing its position and orientation in real-time. Such visual interactions make learning about parametric equations more engaging and interactive.
In addition to enhancing user experience, sliders promote collaboration and communication. Users can share their graphs with others, including the slider settings. This allows recipients to explore the graph, interact with the sliders, and understand the mathematical concepts being illustrated.
In summary, sliders in Desmos are a powerful tool that transforms parametric equations into interactive experiences. By empowering users to control the animation, gain insights, collaborate, and communicate, sliders greatly enhance the value and enjoyment of parametric graphing.
Exporting and Sharing Graphs in Desmos: Collaborate and Communicate Visual Insights
Communicating and sharing graphical representations of mathematical concepts is crucial for effective collaboration and knowledge exchange. With Desmos, you can seamlessly export and share your graphs with others, enabling remote collaboration and enhancing visual storytelling.
Exporting Options
Desmos provides multiple export options to cater to various needs. You can export graphs as images in various formats (PNG, SVG, PDF), ensuring compatibility with different software and platforms. Alternatively, you can export the graph as a link, allowing others to view and interact with it online. This link can be easily shared via email, messaging apps, or social media.
Collaborative Features
For collaborative projects, Desmos offers a user-friendly interface that makes it easy to share and edit graphs. By creating a class or group, you can invite others to join and contribute to the same graph. This collaborative feature streamlines the process of brainstorming, visualizing ideas, and refining concepts as a team.
Enhancing Visual Storytelling
Exported graphs can be integrated into presentations, reports, and other documents to enhance visual storytelling. The high-quality exported images and interactive links enable you to present complex mathematical concepts in an engaging and understandable manner. By incorporating these visual aids, you can captivate your audience and convey your ideas with clarity and precision.
Sharing on Social Media
Desmos also allows you to share your graphs directly on social media platforms, such as Twitter and Facebook. This feature provides a convenient way to reach a wider audience and share your mathematical insights with the world. By including a link to your graph in your social media posts, you can promote collaboration and engage with others who are interested in the same mathematical topics.
Exporting and sharing graphs in Desmos empowers you to collaborate effectively, enhance visual storytelling, and reach a wider audience. With its user-friendly interface and diverse export options, Desmos makes it easy to communicate and share mathematical ideas with others, fostering collaboration and advancing knowledge.