Master Function Graph Sketching: A Comprehensive Guide To Revealing Key Features

Sketching the graph of a function involves understanding the domain and range, identifying asymptotes, finding intercepts, analyzing symmetry, determining extrema, and considering transformations. By following these steps, you can accurately depict the function’s behavior, revealing key features like limits, critical points, and the overall shape of the curve.

• Describe the importance of sketching graphs of functions for understanding function behavior.
• State the purpose of the guide: to provide a comprehensive explanation of how to sketch graphs accurately.

Unveiling the Secrets of Function Graphs: A Step-by-Step Guide to Sketching Mastery

In the realm of mathematics, functions play a pivotal role, describing relationships between variables and revealing hidden patterns in data. At the heart of understanding function behavior lies the art of sketching their graphs, a skill that empowers us to visualize these relationships and gain deeper insights. This comprehensive guide will equip you with the knowledge and techniques to sketch function graphs with precision, unlocking the mysteries of function behavior.

As you embark on this journey, recognize that sketching graphs is not merely an exercise in artistry; it’s a fundamental skill that enhances your understanding of functions and their applications. By delving into the underlying concepts and applying them systematically, you’ll be able to analyze function behavior, predict trends, and make informed decisions based on real-world data.

Understanding the Domain and Range

• Define the domain and range of a function.
• Explain the concepts of independent and dependent variables.
• Describe how to determine the domain and range from a function equation.

Understanding the Domain and Range: The Building Blocks of Function Graphs

When sketching the graph of a function, the first step is to define its domain and range. These two concepts are fundamental to comprehending how a function behaves.

The domain is the set of all possible input values, also known as independent variables, for which the function produces a valid output. Think of it as the “ingredients” you put into a function to get a result.

The range is the set of all possible output values, or dependent variables, that the function can generate. It’s the “result” you get when you plug in a value from the domain.

Determining the domain and range isn’t always straightforward. Sometimes, it’s immediately apparent from the function equation. For instance, in the function f(x) = x^2, the domain is all real numbers because you can square any number. The range, however, is only non-negative numbers because the square of any number is always positive or zero.

In other cases, you may need to consider the function’s properties and restrictions. For example, the function f(x) = 1/x has a domain of all real numbers except zero, because you can’t divide by zero. The range is all real numbers except zero as well, because the reciprocal of any number (except zero) is always a non-zero number.

Understanding the domain and range is crucial for sketching accurate function graphs. It provides the framework within which the function operates, and it helps you identify key features like asymptotes and intercepts.

Asymptotes: A Guide to Understanding Function Behavior

Imagine you’re driving down a road that seems to stretch on forever. Suddenly, a fence appears in the distance, seemingly blocking your path. This is a vertical asymptote, a boundary that your car (or the function’s graph) cannot cross.

Vertical Asymptotes

Vertical asymptotes occur where the function’s denominator is zero. To find them, solve the denominator of the function for x = 0. For example, consider the function f(x) = (x-2)/(x+1). Setting the denominator to zero gives x+1 = 0, or x = -1. This means that the graph of f(x) has a vertical asymptote at x = -1.

Horizontal Asymptotes

Now, envision yourself driving on the interstate, and in the distance, the road seems to level off, gradually converging towards a horizontal line. This is a horizontal asymptote, a line that the function’s graph approaches but never quite touches.

To find horizontal asymptotes, analyze the numerator and denominator as x approaches infinity (x → ∞) or negative infinity (x → -∞). If the ratio of the leading coefficients is non-zero, then y = k is a horizontal asymptote, where k is the constant term of the numerator divided by the constant term of the denominator. For example, the function f(x) = (2x+3)/(x-1) has a horizontal asymptote of y = 2.

Asymptotes provide valuable insights into a function’s behavior. Vertical asymptotes reveal discontinuity points, while horizontal asymptotes indicate the limit of the function as x approaches infinity or negative infinity. Understanding asymptotes is crucial for sketching accurate function graphs and comprehending their characteristics.

Intercepting the Secrets of Functions: Unveiling Their Points of Contact

In the realm of functions, intercepts are the gatekeepers to understanding a graph’s behavior. These pivotal points, where the graph meets the x-axis and y-axis, provide invaluable insights into the function’s characteristics.

X-Intercepts: Zeroing in on the x-axis

To determine the x-intercepts, we embark on a quest to find the values of x where the function’s y-coordinate vanishes. In other words, we set the function’s equation equal to zero, yielding an algebraic equation. Solving this equation reveals the x-intercepts, which are the points where the graph crosses the x-axis.

Y-Intercepts: Ascending to the y-axis

Unveiling the y-intercepts requires a similar approach. This time, we set the function’s x-coordinate equal to zero, resulting in an equation that divulges the values of y where the graph intercepts the y-axis. These points illuminate the function’s initial upward or downward trajectory.

Intercepts: Unveiling Function’s Signatures

Intercepts are not mere dots on a graph; they embody profound information about a function’s behavior. The number of x-intercepts often hints at the function’s degree, while the y-intercept indicates the function’s starting point. Furthermore, intercepts help establish the function’s domain and range, providing boundaries to its realm of possibilities.

In essence, intercepts are the gateway to understanding the intricate dance of functions on a graph. By mastering the art of finding intercepts, we unlock the secrets of a function’s characteristics, paving the way for a comprehensive analysis of its behavior.

Symmetry: Unraveling the Secrets of Function Behavior

When exploring the intricacies of functions, symmetry holds a special allure. Symmetry unveils hidden patterns and provides valuable insights into function behavior. Let’s delve into the world of even and odd functions and discover the concept of the axis of symmetry.

Even Functions: Embracing Symmetry

Even functions possess a remarkable characteristic: they mirror themselves across the y-axis. This means that if you draw a vertical line through the origin, the left and right halves of the graph are identical. The algebraic test for evenness is simple: if f(-x) = f(x) for all values of x in the domain, then the function is even. This symmetry reflects the fact that the function values are unaffected by a change in the sign of the input.

Odd Functions: Chasing Asymmetry

In contrast to even functions, odd functions exhibit a different kind of symmetry. They mirror themselves across the origin, creating a reflection instead of a straight mirror image. The algebraic test for oddness is equally straightforward: if f(-x) = -f(x) for all values of x in the domain, then the function is odd. This symmetry stems from the sign of the function value changing when the sign of the input is reversed.

Axis of Symmetry: The Guiding Line for Even Functions

For even functions, the y-axis serves as the axis of symmetry. This line divides the graph into two congruent halves, with the left half being a mirror image of the right half. The axis of symmetry provides a reference point for understanding the behavior of the function and can help in sketching its graph.

Understanding symmetry is not just an exercise in mathematical aesthetics; it’s a powerful tool for analyzing function behavior. Even and odd functions exhibit unique properties that can simplify calculations, identify important features, and aid in problem-solving. So, the next time you encounter a function, take a moment to consider its symmetry—it might just unlock a deeper understanding of its nature.

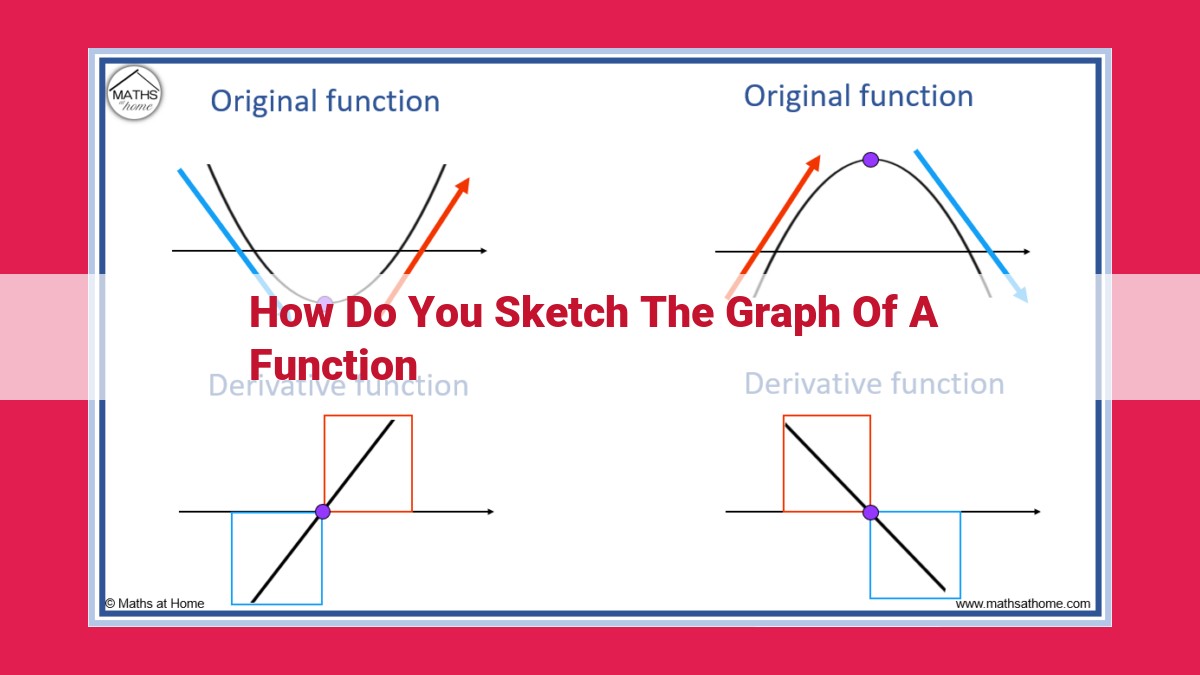
Extrema: Unveiling the Peaks and Valleys of a Function’s Landscape

Extrema, also known as critical points, are special locations on a function’s graph where the function either reaches a maximum or minimum value. Maxima are the highest points, while minima are the lowest points. Identifying extrema is crucial for understanding the overall behavior of a function.

To find extrema, we use the First Derivative Test:

1. Find the critical points: Calculate the derivative of the function and set it equal to zero. The values of the independent variable that make the derivative zero are the critical points.

2. Determine the extrema: At each critical point, evaluate the function. The highest value found is a maximum, while the lowest value is a minimum.

Extrema play a significant role in revealing key features of a function’s graph. They indicate:

• Local maximum and minimum: These points represent the highest and lowest values the function attains within a specific interval.

• Rate of change: At extrema, the derivative is zero, indicating that the function is neither increasing nor decreasing.

• Concavity: Extrema determine whether the function is concave up or down at a specific point.

Understanding extrema is essential for sketching accurate graphs. They help identify crucial points that shape the function’s overall trajectory, making it easier to visualize and analyze its behavior.

Understanding Function Transformations: The Art of Shaping Graphs

When it comes to sketching the graph of a function, transformations are the magic wand that enable us to manipulate and shape the graph to reveal its hidden characteristics. These transformations allow us to translate, stretch, shrink, and reflect graphs effortlessly, creating a kaleidoscope of possibilities.

• Translations: Think of translations as relocating the graph on the coordinate plane. Moving the graph right or left along the x-axis is a horizontal translation, while moving it up or down along the y-axis is a vertical translation.

• Dilations: Dilations are like using a magnifying glass to stretch or shrink the graph. A dilation with a factor greater than one enlarges the graph, while a factor less than one makes it smaller.

• Reflections: Reflections are just as they sound – they mirror the graph across an axis. Reflecting across the x-axis flips the graph upside down, while reflecting across the y-axis flips it from left to right.

The beauty of transformations lies in their ability to be combined, creating intricate patterns. For instance, a translation followed by a dilation can shift and enlarge the graph simultaneously. By experimenting with different combinations, you can create graphs that resemble works of art.

Remember, understanding function transformations is the key to unlocking the full potential of graph sketching. They allow us to manipulate graphs with precision, revealing their hidden features and patterns. With practice, you’ll become a master of transformations, painting beautiful graphs that tell the stories of functions.