Discover Limit Calculations With Desmos: A Comprehensive Guide To Asymptotes And Continuity

To use the limit operator in Desmos, [lim(expression, variable, value)], enter the expression to be evaluated, the variable approaching the limit, and the value of the limit. For example, to calculate the limit of (x^2 – 1)/(x – 1) as x approaches 1, use: lim((x^2 – 1)/(x – 1), x, 1). Desmos can also be used to explore related concepts such as asymptotes, continuity, and derivatives, providing a comprehensive tool for limit exploration.

In the realm of mathematics, limits stand as beacon of discovery, shedding light on the enigmatic behavior of functions as they approach infinity or specific inputs. These mathematical entities are not mere abstractions; they hold immense significance in various fields, including calculus, analysis, and physics.

Limits are used to describe the asymptotic behavior of functions, revealing whether they converge to a finite value, diverge to infinity, or oscillate between two values. Understanding limits allows us to make predictions about the behavior of functions even beyond the immediate confines of their domains.

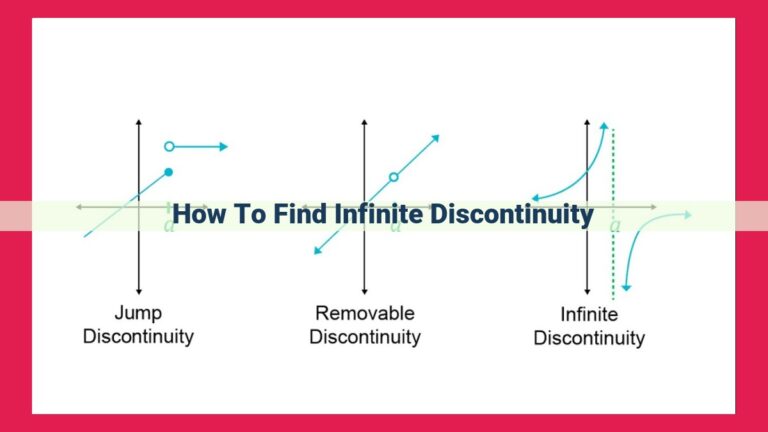
Furthermore, limits are intimately connected to other fundamental mathematical concepts such as asymptotes, continuity, and derivatives. Asymptotes represent lines that functions approach but never intersect, indicating the presence of a limit. Continuity ensures that functions have no “jumps” or breaks, while derivatives measure the instantaneous rate of change of functions. By integrating these concepts, we gain a comprehensive understanding of the local and global behavior of functions.

Syntax of the lim Operator in Desmos: Unlocking the Secrets of Mathematical Boundaries

In the realm of mathematics, limits stand as gatekeepers to understanding the true nature of functions as they approach specific values or infinity. Desmos, the online graphing calculator, empowers us to explore these boundaries with its powerful lim operator.

The Essential Elements of the lim Syntax

The syntax of the lim operator revolves around three key elements: the expression, the variable, and the value. The expression represents the function we wish to evaluate the limit of, while the variable defines the input that approaches the desired value. Finally, the value specifies the point at which we want to calculate the limit.

For instance, to find the limit of the function f(x) = x^2 as x approaches 2, we would enter the following expression in Desmos:

lim(x^2, x, 2)

Arguments galore: Exploring the Versatility of the lim Operator

Desmos offers a wide range of arguments that can enrich our limit exploration. These arguments include:

• Left-Hand Limit (lim_from_left): Evaluates the limit as the variable approaches the value from the left side of the number line.
• Right-Hand Limit (lim_from_right): Evaluates the limit as the variable approaches the value from the right side of the number line.
• Two-Sided Limit (lim): Evaluates the limit as the variable approaches the value from both the left and right sides.
• Infinity (oo or -oo): Calculates the limit as the variable approaches positive or negative infinity, respectively.

Harnessing the Power of Desmos to Illuminate Limits

Using the lim operator in Desmos is a breeze. Simply enter the expression, variable, and value into the calculator’s input field. Desmos will swiftly compute the limit and display the result.

For example, to find the left-hand limit of the function f(x) = 1/x as x approaches 0, we can enter the following expression:

lim_from_left(1/x, x, 0)

Desmos will promptly reveal the result as -infinity.

Unveiling the Secrets of Limits with Desmos

In the realm of mathematics, limits hold immense significance. They allow us to explore the behavior of functions as they approach specific values. Desmos, a powerful graphing calculator, empowers us to calculate limits with ease.

Navigating the Syntax of the lim Operator

Desmos utilizes the lim operator to evaluate limits. This operator follows a precise syntax:

lim(expression, variable, value)

• Expression: The mathematical expression whose limit is being determined.
• Variable: The variable approaching the specified value.
• Value: The value towards which the variable approaches.

Step-by-Step Guide to Evaluating Limits in Desmos

1. Open Desmos: Navigate to www.desmos.com.

2. Enter the Expression: Type the mathematical expression whose limit you wish to find in the Desmos input field.

3. Specify the Variable: After the expression, include the variable that approaches the specified value. Separate them with a comma.

4. Define the Value: Lastly, specify the value that the variable approaches. This is separated from the variable by another comma.

5. Calculate the Limit: Click the “Evaluate” button or press Enter to calculate the limit.

For example, to find the limit of the function f(x) = (x^2 – 1)/(x – 1) as x approaches 1, enter the following expression in Desmos:

lim((x^2 - 1)/(x - 1), x, 1)

6. Interpret the Result: Desmos will display the calculated limit. Analyze the result to understand the behavior of the function as the variable approaches the specified value.

Exploring Related Concepts with Desmos

In the realm of mathematics, limits hold immense significance, revealing the behavior of functions as they approach specific values. While the lim operator in Desmos empowers us to calculate limits with ease, its true power lies in its ability to explore a tapestry of related concepts that enrich our understanding of these mathematical marvels.

Graphing Functions for Limit Analysis

By graphing functions in Desmos, we can visually observe their behavior as they approach a particular point. Asymptotes, those vertical or horizontal lines that the graph approaches but never touches, become evident, providing insights into the function’s behavior at infinity. The presence of holes or discontinuities in the graph can also signal that the limit does not exist at that point.

Asymptotes and Limit Evaluation

Asymptotes play a crucial role in limit evaluation. Vertical asymptotes indicate that the function approaches infinity or negative infinity as the independent variable approaches a specific value. Horizontal asymptotes, on the other hand, suggest that the function approaches a constant value as the independent variable approaches infinity or negative infinity. By observing the presence of asymptotes in the graph of a function, we can make informed predictions about its limits.

Continuity and Limit Existence

Continuity examines the smooth transition of a function at a given point. If the function is continuous at that point, its graph will have no “jumps” or “breaks,” and the limit at that point will exist. Conversely, if the function is discontinuous at that point, its graph will exhibit a sudden change, and the limit may not exist or may be different from the value of the function at that point.

Derivatives and Limit Evaluation

Derivatives measure the rate of change of a function. By examining the derivative of a function at a given point, we can determine whether the function is increasing or decreasing as it approaches that point. This information can provide valuable insights into the existence and value of the limit at that point.

Desmos emerges as an invaluable tool for limit exploration. By harnessing its capabilities to visualize functions, identify asymptotes, assess continuity, and leverage derivatives, we gain a multifaceted understanding of the behavior of functions as they approach various points. This exploration unveils the intricate tapestry of relationships between limits and related concepts, empowering us to navigate the mathematical landscape with greater confidence and insight.