Kinetic Energy: Understanding The Energy Of Motion
Kinetic energy, representing the energy of motion, is measured in joules (J). This unit honors physicist James Prescott Joule and represents the energy expended by a force of one newton acting over a distance of one meter. Joules can be interchanged with Newton-meters (Nm) and ergs, where 1 J = 1 Nm and 1 J = 10^7 ergs. Kinetic energy depends on both mass and velocity, as per the formula KE = 1/2 * m * v², where KE is kinetic energy, m is mass, and v is velocity.
Kinetic Energy: The Energy of Motion
In the realm of physics, energy takes center stage, and among its diverse forms, kinetic energy stands out as the embodiment of energy in motion. This concept is so fundamental to our everyday experiences that we often take it for granted. But let’s delve into the captivating world of kinetic energy and unravel its secrets.
Imagine a speeding car zooming past you. The kinetic energy it possesses gives it the ability to move, and its magnitude depends on two crucial factors: mass (m) and velocity (v). The heavier the car and the faster it travels, the greater its kinetic energy. It’s like a weightlifter with a heavy stack of weights – the more weight they lift and the faster they move it, the more energy they exert.
The relationship between kinetic energy and mass and velocity is precisely captured by the formula: KE = 1/2 * m * v². This equation reveals that kinetic energy is directly proportional to mass and the square of velocity. That means doubling the mass of an object doubles its kinetic energy, while doubling its velocity quadruples it. In other words, speed matters a lot!
Kinetic Energy: The Energy of Motion
Kinetic energy is the energy possessed by an object due to its motion. It’s an intrinsic property of moving objects, and its magnitude depends on both the mass of the object and its velocity.
The relationship between kinetic energy and the motion of an object is described by the formula KE = 1/2 * m * v², where KE is kinetic energy, m is the mass of the object, and v is its velocity. This equation illustrates how kinetic energy is directly proportional to both mass and the square of velocity.
Mass is a measure of the object’s resistance to acceleration. The greater the mass, the greater the force required to accelerate the object, and consequently, the more kinetic energy it possesses. On the other hand, velocity is a measure of the object’s speed and direction. The faster the object is moving, the greater its kinetic energy.
Kinetic energy plays a crucial role in understanding the behavior of moving objects. For example, in a collision, the kinetic energy of the colliding objects is converted into other forms of energy, such as sound, heat, or deformation. Additionally, kinetic energy is used to explain the motion of fluids, such as the flow of water or air.
Understanding kinetic energy is essential for comprehending the dynamics of moving objects, and its importance extends across various scientific disciplines, from physics to engineering.
Kinetic Energy: The Energy of Motion
In the realm of physics, energy manifests in myriad forms, and one of the most fundamental is kinetic energy. It’s the energy an object possesses due to its motion, a concept that has fascinated scientists and engineers for centuries.
Kinetic energy is directly proportional to an object’s mass and the square of its velocity. The greater the mass of an object or the faster it moves, the more kinetic energy it carries. This relationship is mathematically expressed as:
KE = 1/2 * m * v²
where KE represents kinetic energy, m is the mass of the object, and v is its velocity.
One of the key concepts to grasp about kinetic energy is its unit of measurement, the joule (J), named after the renowned physicist James Prescott Joule. A joule is defined as the energy used to exert a force of one newton over a distance of one meter.
In essence, a joule is a measure of the work done or the energy transferred. To illustrate, imagine lifting a 1-kilogram object one meter into the air. This action requires 9.8 joules of energy, as you’re overcoming the gravitational force pulling the object down.
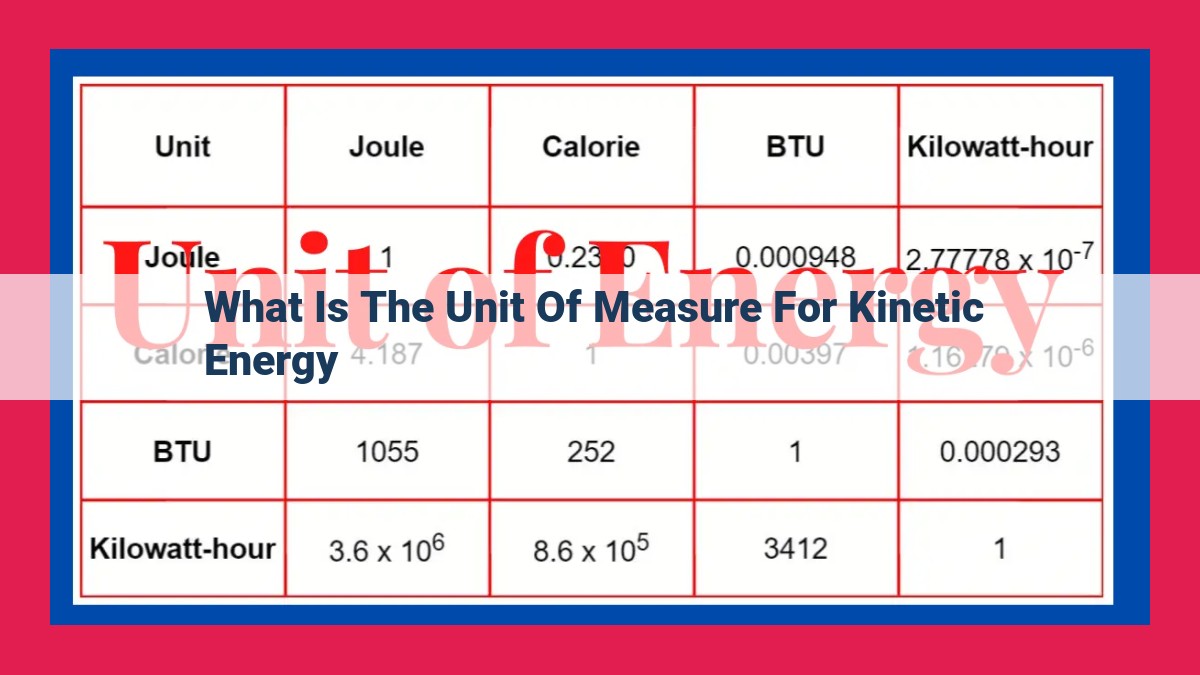
The joule is a SI unit, meaning it’s part of the International System of Units, the globally recognized standard for scientific measurements. Other units can also be used to express kinetic energy, such as the newton-meter (N m) and the erg. One joule is equivalent to one newton-meter and 10 million ergs.
Understanding the unit of kinetic energy is crucial for quantifying and comparing the motion of objects. It empowers us to make calculations, solve problems, and gain insights into the dynamics of our physical world. So, the next time you observe an object in motion, remember the joule, a testament to the energy inherent in its movement.
Understanding Kinetic Energy: The Energy of Motion
Kinetic energy is the energy possessed by an object in motion. It depends on two crucial factors: mass and velocity. The mass of an object represents its resistance to acceleration, while velocity measures the speed and direction of its motion.
Energy of Motion
Kinetic energy embodies the energy of motion. The faster an object moves, the greater its kinetic energy. Similarly, the more massive an object, the higher its kinetic energy. This relationship highlights the profound interplay between mass and velocity in determining an object’s kinetic energy.
Unit of Measure: Joule (J)
The standard unit of kinetic energy is the joule (J). It is named after James Prescott Joule, who made significant contributions to the understanding of energy and heat. A joule represents the amount of energy required to exert a force of one newton through a distance of one meter.
Equivalent Units
While the joule is the most commonly used unit for kinetic energy, other units are also employed in certain contexts. These include the Newton-meter (N m) and the erg.
- Newton-meter (N m): This unit is defined as the energy required to exert a force of one newton through a distance of one meter. It is equivalent to one joule.
- Erg: An erg is a smaller unit of energy, equal to one dyne-centimeter. One joule is equivalent to 10,000,000 ergs.
Understanding the relationship between kinetic energy, mass, and velocity is crucial for comprehending the mechanics of motion. The formula KE = 1/2 * m * v² succinctly expresses this relationship, where KE represents kinetic energy, m denotes mass, and v signifies velocity.
Unveiling the Symphony of Kinetic Energy: Mass, Velocity, and the Dance of Motion
In the realm of physics, energy manifests itself in myriad forms, and kinetic energy stands out as the embodiment of motion. It’s the driving force behind the flow of rivers, the soaring of birds, and the pulsation of our own hearts.
The essence of kinetic energy lies in its direct proportionality to both an object’s mass (m) and the square of its velocity (v). This intimate relationship is encapsulated in the formula:
KE = 1/2 * m * v²
Mass: The Inertia’s Anchor
Mass, a fundamental property of matter, measures an object’s resistance to acceleration. The greater the mass, the harder it is to set an object in motion or alter its course. Think of a colossal boulder compared to a nimble pebble—the boulder’s substantial mass makes it more challenging to budge than its diminutive counterpart.
Velocity: The Speed and Direction of Motion
Velocity, on the other hand, captures the speed and direction of an object’s movement. The faster an object travels, the greater its kinetic energy. Moreover, the direction of motion also plays a role: two objects with equal speeds but moving in opposite directions possess equal but opposite kinetic energies.
Interplay of Mass and Velocity: A Dynamic Duo
The formula for kinetic energy reveals the intricate interplay between mass and velocity. As mass increases, kinetic energy scales linearly. Conversely, velocity has an exponential effect on kinetic energy. Doubling the velocity of an object quadruples its kinetic energy.
This relationship underscores the significance of mass and velocity in determining the energy of motion. A massive object moving at a high speed carries immense kinetic energy, while a lighter object traveling at a slower speed possesses a lower amount of kinetic energy.
Understanding the connection between kinetic energy, mass, and velocity is crucial for comprehending the dynamics of our physical world. It enables us to calculate the forces required to accelerate objects, predict the outcomes of collisions, and appreciate the interplay of matter and motion in myriad contexts.