Kinetic Energy: A Comprehensive Guide To Mass, Velocity, And Energy

Kinetic energy is influenced by the mass and velocity of an object. Heavier objects have greater kinetic energy, and objects moving faster also possess more kinetic energy. The gravitational force acting on an object can affect its kinetic energy, as can its weight and inertia. The direction of an object’s motion, including its displacement and angle, can also impact its kinetic energy. The formula for kinetic energy, KE = 1/2 * mv², illustrates how these factors—mass and velocity—determine the kinetic energy of an object.

Kinetic Energy: Unveiling the Energy of Motion

What is Kinetic Energy?

Imagine a speeding bullet or a rolling bowling ball. What gives these objects their ability to do work or cause damage? The answer lies in kinetic energy, the energy an object possesses solely due to its motion. It’s the hidden power behind every movement we see around us.

Kinetic energy (KE) is a scalar quantity, meaning it has only magnitude and no direction. It is directly proportional to an object’s mass m and the square of its velocity v. Mathematically, it is expressed as:

KE = 1/2 * m * v^2

The Significance of Kinetic Energy

Kinetic energy plays a crucial role in our daily lives and in the world around us. It:

• Drives machines: Engines convert fuel into kinetic energy, which powers cars, airplanes, and other machines.
• Causes damage: A moving object with high kinetic energy can inflict significant damage upon impact, like a car crash or a meteorite striking Earth.
• Is conserved in collisions: In an isolated system, the total kinetic energy of objects remains constant before and after a collision, although it may be transferred between objects.
• Provides insights into motion: By measuring an object’s kinetic energy, scientists can determine its velocity, mass, and even its momentum, which is a crucial quantity in physics.

Present the formula for kinetic energy: KE = 1/2 * mv².

Understanding Kinetic Energy: The Essence of Motion

Kinetic energy, the energy of motion, is an essential concept in physics that plays a pivotal role in our everyday lives. Imagine a rolling ball, a speeding car, or even the beating of your heart; these are all examples of kinetic energy in action.

At its core, kinetic energy (KE) is defined as the energy an object possesses due to its motion. It depends on two crucial factors: mass (m) and velocity (v). The formula for kinetic energy is a cornerstone of physics: KE = 1/2 * mv².

The Influence of Mass on Kinetic Energy

Mass, a measure of an object’s resistance to acceleration, heavily influences its kinetic energy. Consider two objects of different masses traveling at the same speed. The object with greater mass will possess higher kinetic energy due to its greater inertia. Inertia is the tendency of an object to resist any change in its motion.

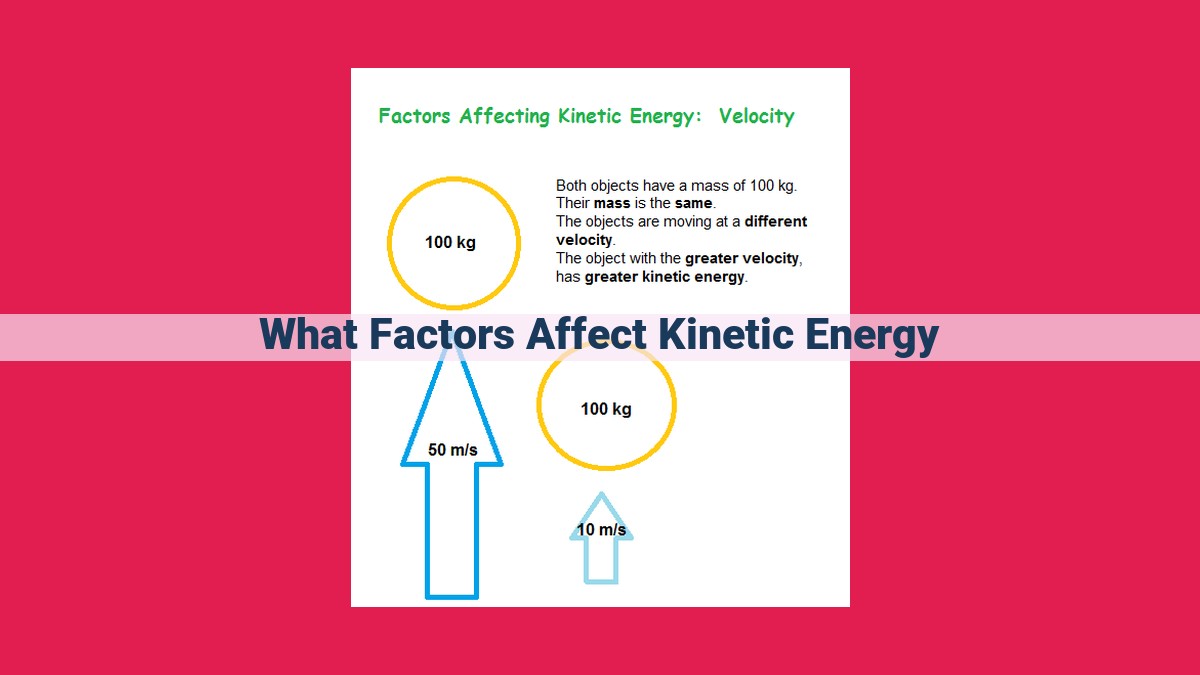
The Role of Velocity on Kinetic Energy

Velocity, a vector quantity that includes both speed and direction, also plays a significant role in determining kinetic energy. As an object’s speed increases, so does its kinetic energy. Acceleration, the rate at which velocity changes, also affects kinetic energy. Objects with greater acceleration gain kinetic energy more rapidly.

The Importance of Direction in Kinetic Energy

Kinetic energy is a scalar quantity, meaning it has only magnitude and no direction. However, the direction of velocity is crucial in determining the net kinetic energy in a system. Imagine two objects colliding head-on; the resulting kinetic energy will be different than if they collide at an angle.

Real-World Applications of Kinetic Energy

Kinetic energy is a fundamental concept in numerous real-world applications, from power plants to everyday devices. Understanding the physics behind kinetic energy empowers us to harness its potential and create innovative solutions for various challenges.

The Influence of Gravitational Force on Kinetic Energy

Kinetic energy, the energy of motion, plays a crucial role in the dynamics of our world. Gravitational force, an invisible yet powerful force that draws objects towards each other, profoundly influences the kinetic energy of objects.

Imagine a ball rolling down a hill. As it descends, the gravitational force pulls it downwards, causing it to accelerate. This acceleration translates into an increase in kinetic energy, as the ball’s velocity increases. The greater the gravitational force, the faster the acceleration and the higher the kinetic energy of the ball.

This interplay between gravitational force and kinetic energy is not limited to balls rolling down hills. It governs the motion of planets orbiting the Sun, satellites circling the Earth, and even the flight of rockets.

For instance, when a rocket is launched into space, its fuel combusts, generating thrust that propels it upwards against the pull of Earth’s gravity. As it overcomes gravity and gains altitude, its kinetic energy increases significantly.

On the flip side, as the rocket ascends, the gravitational force acting upon it gradually weakens. This reduction in force results in a decrease in acceleration, and consequently, a reduction in kinetic energy. Eventually, the rocket reaches a point where the force of gravity is negligible, and its kinetic energy becomes constant.

The relationship between gravitational force and kinetic energy is fundamental to understanding the dynamics of motion in our universe. From the rolling ball to the soaring rocket, gravitational force plays a pivotal role in shaping the kinetic energy of objects, influencing their trajectories and potential for motion.

Kinetic Energy: A Comprehensive Guide

Understanding Kinetic Energy

Kinetic energy, the energy of motion, is a fundamental concept in physics that governs the behavior of moving objects. It arises from the object’s velocity and mass. The formula for kinetic energy is KE = 1/2 * mv², where KE represents kinetic energy, m represents the object’s mass, and v represents its velocity.

The Impact of Mass on Kinetic Energy

Mass plays a crucial role in determining an object’s kinetic energy. The more massive an object, the higher its kinetic energy will be for the same velocity. This relationship is evident in the formula KE = 1/2 * mv². As mass increases, so does kinetic energy.

Gravitational Force

Gravitational force, the attraction between objects with mass, further influences kinetic energy. On Earth, an object’s weight, the gravitational force acting upon it, is proportional to its mass. Therefore, heavier objects have more kinetic energy than lighter objects when moving at the same speed.

Inertia

Inertia, the resistance of an object to change its motion, is also affected by mass. Massive objects have greater inertia, which makes them more difficult to accelerate. Consequently, massive objects require more energy to reach the same kinetic energy as lighter objects.

The Influence of Velocity on Kinetic Energy

Velocity, the speed and direction of an object’s motion, has a significant impact on its kinetic energy. The faster an object moves, the higher its kinetic energy. Doubling an object’s velocity increases its kinetic energy fourfold. This relationship is demonstrated by the formula KE = 1/2 * mv².

Speed

Speed, the magnitude of velocity, directly influences kinetic energy. The faster an object travels, the more kinetic energy it possesses. This principle is evident in everyday life, such as the greater impact of a high-speed car crash compared to a low-speed collision.

Acceleration

Acceleration, the rate of change in velocity, also plays a role in kinetic energy. As an object accelerates, its kinetic energy increases. This increase is due to the work done by the force causing the acceleration.

Momentum

Momentum is a measure of an object’s motion, combining its mass and velocity. Kinetic energy and momentum are closely related, with kinetic energy being proportional to the square of the momentum. This relationship is expressed by the equation KE = p²/2m, where p represents momentum.

Inertia: Describe how inertia affects the acceleration and kinetic energy of an object.

Inertia: The Obstacle to Motion

Inertia, a concept introduced by Sir Isaac Newton in his first law of motion, refers to an object’s inherent reluctance to change its state of motion. Whether an object is at rest or moving at a constant velocity, it possesses inertia, which resists any attempt to alter its momentum.

Kinetic energy, on the other hand, is a measure of an object’s energy due to its motion. According to the formula KE = 1/2 * mv², the kinetic energy of an object is directly proportional to its mass (m) and the square of its velocity (v).

Inertia’s Impact on Acceleration

Inertia plays a crucial role in determining an object’s acceleration, the rate at which its velocity changes over time. Imagine a car at rest; its inertia resists the application of force, making it difficult to accelerate it. However, once the car is in motion, its inertia resists any change in velocity, making it challenging to brake or change its direction.

Inertia and Momentum

Momentum is the measure of an object’s mass in motion, and it is directly proportional to its kinetic energy. Inertia acts to conserve momentum, which means that an object’s momentum remains constant unless an external force acts upon it.

Examples of Inertia in Everyday Life

Inertia is a ubiquitous force in our daily experiences. When you try to push a heavy object, its inertia resists your efforts, making it challenging to move. When you stop pedaling your bicycle, its inertia keeps it gliding forward for a short while. Even when you simply stand still, your inertia prevents you from suddenly falling over.

Inertia is a fundamental property of matter that shapes our interactions with the world around us. It influences an object’s acceleration, kinetic energy, and momentum, affecting everything from the motion of cars to the flow of fluids. Understanding inertia allows us to make informed decisions in various aspects of our lives, from driving safely to designing efficient machinery.

The Nexus Between Speed and Kinetic Energy

In our quest to unravel the enigmatic tapestry of physics, we encounter a fundamental concept that intertwines energy and motion: kinetic energy. As we probe deeper into this phenomenon, let us pause and delve into the fascinating relationship between kinetic energy and its pivotal component: speed.

The essence of kinetic energy lies in its ability to quantify the energy possessed by an object in motion. Imagine a ball rolling down a slope, its speed increasing with each passing moment. This surge in speed corresponds to a corresponding increase in kinetic energy. The underlying mathematical formula, KE = 1/2 * mv², elegantly captures this intricate connection.

Speed, represented by the variable v in this equation, exerts a profound influence on kinetic energy. The faster an object moves, the greater its kinetic energy. This relationship holds true regardless of the mass of the object. Whether it be a minuscule pebble or a colossal boulder, the kinetic energy amplifies with increasing speed.

To illustrate this concept further, consider a car speeding down a highway. As it accelerates, its velocity rises, and so does its kinetic energy. Conversely, when the car decelerates, its kinetic energy diminishes proportionally. This interplay between speed and kinetic energy highlights the dynamic nature of this physical quantity.

Acceleration: Discuss how acceleration affects the kinetic energy of an object.

Acceleration: Fueling Kinetic Energy

Imagine a race car hurtling down the track, its engine roaring with power. As it accelerates, something extraordinary happens within the car’s framework: its kinetic energy skyrockets. Kinetic energy, measured in joules, is the energy an object possesses due to its motion. And as we delve deeper into the world of physics, we uncover a profound relationship between acceleration and kinetic energy.

Acceleration, the rate at which an object’s velocity changes over time, plays a pivotal role in shaping an object’s kinetic energy. The simple yet elegant formula for kinetic energy encapsulates this relationship: KE = 1/2 * mv², where m is the object’s mass and v its velocity. As acceleration increases, it triggers a cascade of events that propel the object to greater speeds. With each surge in velocity, the object’s kinetic energy rises exponentially, reflecting the increased energy it now possesses due to its faster movement.

For instance, in a drag race, the cars that accelerate the quickest often emerge victorious. The reason? By harnessing their engines’ power to accelerate rapidly, they build up substantial kinetic energy that propels them towards the finish line with unmatched velocity.

Acceleration not only dictates an object’s speed but also its momentum. Momentum is a vector quantity, meaning it has both magnitude (the mass of the object times its velocity) and direction. As an object accelerates, its momentum changes accordingly. This interconnectedness between acceleration, kinetic energy, and momentum underscores the intricate interplay of these physical concepts.

In summary, acceleration acts as a catalyst for kinetic energy, enabling objects to amass more energy as they move faster. From the roaring engines of race cars to the subtle movements of everyday life, acceleration is the driving force behind the ever-changing kinetic energy of our world.

Momentum: The Twin of Kinetic Energy

In the realm of physics, momentum stands beside its sibling, kinetic energy, as an inseparable pair. Momentum measures the mass in motion, while kinetic energy quantifies the energy of that motion. The relationship between these two fundamental concepts is profound.

Imagine a colossal bowling ball hurtling down the lane at blazing speed. Its momentum is immense, determined by its mass and the velocity with which it rolls. As it crashes into the pins, some of its kinetic energy, the energy stored in its motion, is transferred to the pins, which in turn gain momentum.

The connection between momentum and kinetic energy can be expressed mathematically through a simple formula:

Momentum (p) = Mass (m) x Velocity (v)

Kinetic Energy (KE) = 1/2 x Mass (m) x Velocity (v)²

As you can see, momentum is directly proportional to velocity, while kinetic energy is proportional to the square of velocity. This implies that a small change in velocity can have a dramatic impact on kinetic energy.

In the bowling alley example, the bowling ball’s kinetic energy is vastly greater than its momentum because its velocity is squared in the kinetic energy formula. Therefore, a small increase in speed results in a significant increase in kinetic energy, which is evident as the bowling ball obliterates the pins.

Understanding the relationship between momentum and kinetic energy is crucial for grasping the dynamics of our world. From the flight of a billiard ball to the motion of celestial bodies, these two quantities play a vital role in shaping the universe we experience.

Unraveling the Enigma of Kinetic Energy: A Comprehensive Guide

Embarking on a Journey into Motion

In the realm of physics, kinetic energy holds a pivotal role, defining the energy possessed by an object due to its motion. Imagine a speeding bullet, its relentless trajectory fueled by the unseen force of kinetic energy. Defined as KE = 1/2 * mv², it reveals the intimate connection between the object’s mass and velocity.

The Dance of Mass and Kinetic Energy

Mass, the unwavering essence of matter, plays a profound role in shaping kinetic energy. Gravitational force, an irresistible cosmic pull, influences the amount of kinetic energy an object can possess. Weight, a measure of gravitational force acting on an object, is directly proportional to kinetic energy. Inertia, the obstinate resistance to changes in motion, dictates how readily an object accelerates, ultimately impacting its kinetic energy.

Velocity’s Enigmatic Influence

Velocity, the vibrant expression of motion, exerts a transformative effect on kinetic energy. Speed, the velocity’s magnitude, holds a quadratic relationship with kinetic energy, while acceleration, the rate of velocity change, serves as a catalyst for energy conversion. Momentum, the product of mass and velocity, mirrors kinetic energy, revealing their intertwined nature.

The Nexus of Direction and Kinetic Energy

While often overlooked, direction plays a subtle yet crucial role in kinetic energy. Displacement, the vector representing an object’s change in position, influences its kinetic energy. The angle of motion, relative to a reference point, can alter the object’s kinetic energy by modifying the magnitude of its velocity vector. Understanding this intricate relationship unlocks the secrets of kinetic energy’s dynamic nature.

Angle: Unraveling the Impact on Kinetic Energy

Kinetic energy, a measure of an object’s motion, depends not only on its mass and velocity but also on the direction of motion. The angle of motion plays a crucial role in determining the object’s kinetic energy.

Consider a ball thrown upward at an angle. As it rises, its vertical velocity decreases due to gravity, reducing its kinetic energy in that direction. However, its horizontal velocity remains constant, resulting in a non-zero kinetic energy component in the horizontal direction.

The angle of projection significantly influences the ball’s kinetic energy. A ball thrown at a high angle will spend more time in the air, resulting in a greater reduction in vertical kinetic energy compared to a ball thrown at a low angle. Conversely, a low-angle projection minimizes the vertical kinetic energy loss, allowing the ball to maintain a larger horizontal kinetic energy component.

In the context of circular motion, the angle of motion is vital. An object moving in a circular path experiences centripetal force, causing it to accelerate and change direction. This change in direction results in a change in kinetic energy as the object’s velocity vector changes.

Understanding the angle’s influence on kinetic energy is crucial in various applications, including projectile motion, orbital mechanics, and collisions. Engineers and physicists rely on these principles to design efficient systems and predict object behavior in complex environments.

Understanding Kinetic Energy: A Journey into Motion

Kinetic energy, the energy of movement, is fundamental to our understanding of the physical world. Its formula, KE = 1/2 * mv², reveals the critical influence of mass and velocity on an object’s kinetic energy.

The Dance of Mass and Kinetic Energy

Mass, a measure of the amount of matter, plays a vital role in determining kinetic energy. Heavier objects, with greater mass, possess more kinetic energy than lighter ones when moving at the same speed. Imagine a bowling ball and a baseball rolling down a hill; the bowling ball will have significantly more kinetic energy due to its greater mass.

Velocity’s Dynamic Impact

Velocity, a vector quantity involving both speed and direction, has a profound impact on kinetic energy. As an object’s speed increases, so too does its kinetic energy, albeit quadratically. A car traveling at twice the speed will have four times the kinetic energy.

The Connection between Momentum and Kinetic Energy

Momentum, a measure of an object’s motion, is directly proportional to its kinetic energy. An object with greater momentum, indicating more mass or velocity, will have higher kinetic energy. This relationship highlights the interdependence of mass and velocity in determining an object’s kinetic energy.

Direction and Kinetic Energy: A Subtle Dance

While kinetic energy is independent of the direction of motion, the angle of movement can affect its rate of change. An object thrown upwards will have maximum kinetic energy at launch and zero kinetic energy at its peak height. This is due to the change in velocity caused by the influence of gravity.

The Velocity Vector: A Direction of Energy

The velocity vector, a quantity that specifies both the speed and direction of motion, provides context for an object’s kinetic energy. Objects with identical speed but different velocity vectors will have the same kinetic energy magnitude but different directional components. Understanding the velocity vector allows us to fully comprehend an object’s kinetic energy.