Unveiling The Base Of An Isosceles Triangle: Essential Methods And Applications
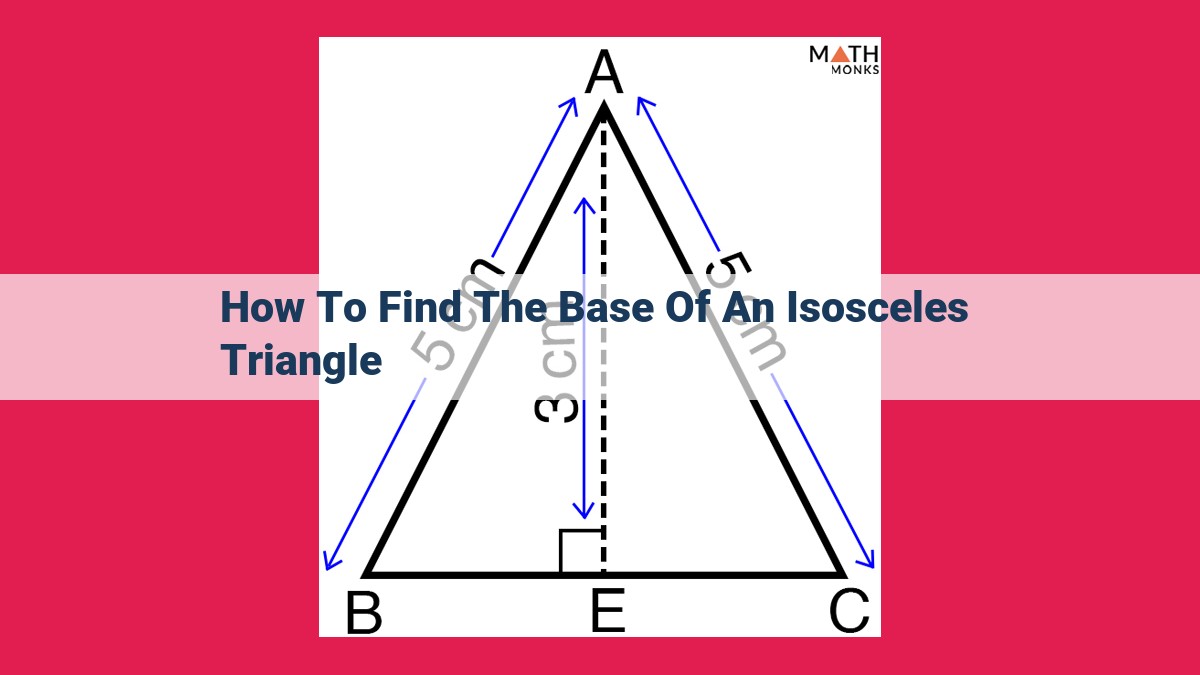
To find the base of an isosceles triangle, leverage its equal sides. Draw the altitude from the vertex opposite the base, dividing the triangle into two congruent right triangles. Apply the Pythagorean theorem to one of these right triangles to solve for the altitude. Knowing the altitude and one side length, use the Pythagorean theorem again to find the length of half the base. Alternatively, for triangles with known sides and an angle, the Law of Cosines can directly determine the base length. Understanding isosceles triangle properties, altitude, and the Pythagorean theorem is crucial for these methods. Applications include finding length in various fields, such as geometry, architecture, and surveying.
Determining the Base Length of an Isosceles Triangle: A Guide for Geometry Enthusiasts
In the realm of geometry, isosceles triangles, with their captivating symmetry and enigmatic nature, have fascinated mathematicians for centuries. Defined by the equal length of two sides, these triangular wonders pose an intriguing challenge: discovering the length of their hidden base. In this comprehensive guide, we embark on a journey to uncover the secrets of isosceles triangles, exploring various methods to unravel the elusive base length.
Prerequisite Concepts
Before delving into the captivating world of isosceles triangles, it is essential to establish a firm foundation. Familiarize yourself with the properties that govern these geometric marvels, including the fundamental principle that the angles opposite to the congruent sides are also congruent. Additionally, grasp the concept of altitude, the perpendicular segment that connects a vertex to the opposite side, bisecting it into two congruent right triangles.
Embracing the Power of the Pythagorean Theorem
Prepare to witness the magic of the Pythagorean theorem, a powerful tool that empowers us to determine side lengths within right triangles. This theorem illuminates the squared lengths relationship between the hypotenuse (longest side) and the other two sides. Harnessing this knowledge, we can unravel the hidden dimensions of isosceles triangles by strategically employing right triangles.
Prerequisite Concepts for Finding the Base of an Isosceles Triangle
Before we embark on our quest to determine the base of an isosceles triangle, let’s first refresh our understanding of some fundamental concepts that will serve as our trusty tools.
Properties of Isosceles Triangles
As the name suggests, isosceles triangles hold a secret: they possess two equal sides. This special characteristic sets them apart from other triangle types. So, if you’re ever faced with a triangle with two identical sides, rest assured, it’s an isosceles triangle.
Definition of Altitude
Now, let’s turn our attention to altitude. In the realm of triangles, altitude refers to the perpendicular distance from a vertex to the opposite side. In the case of isosceles triangles, the altitude bisects the base, creating two equal segments. This trusty altitude will be our guide in unlocking the secrets of the base length.
Discovering the Pythagorean Theorem: A Journey into Right Triangle Geometry
In the intricate world of geometry, isosceles triangles hold a special place, distinguished by their two equal sides. For those seeking to determine the length of the enigmatic base of these fascinating shapes, the Pythagorean theorem emerges as an invaluable tool.
The Pythagorean theorem, a cornerstone of right triangle geometry, reveals the profound relationship between the hypotenuse (the longest side opposite the right angle) and the other two sides. In the case of an isosceles triangle, where two sides are equal, the Pythagorean theorem takes on a unique significance.
Picture an isosceles triangle, its congruent sides stretching out like twins. Imagine drawing an altitude, a line perpendicular to the base that divides the triangle into two identical right triangles. The Pythagorean theorem then steps into the spotlight, illuminating the connection between the side length, altitude, and the length we seek – the base.
The formula encapsulates the theorem’s essence: (side length)² + (altitude)² = (hypotenuse)². Using this potent equation, we can unravel the mystery of the base by extracting its value from the given side length and altitude measurements.
Delving deeper into the theorem’s workings, we encounter the hypotenuse, a crucial component in the triangle’s geometry. The hypotenuse signifies the longest side, always lying opposite the right angle. In the context of an isosceles triangle, with its two equal sides, the hypotenuse becomes the third distinct side, holding the key to unlocking the base’s length.
Thus, the Pythagorean theorem emerges as an indispensable instrument for exploring the depths of isosceles triangles, guiding us in our quest to determine the elusive base. Its power lies in its ability to illuminate the hidden relationships within these geometric marvels, making it a cornerstone of right triangle geometry.
Finding the Base of an Isosceles Triangle Using Altitude and Side Length
Step 1: Draw the Altitude and Divide the Triangle
To find the base of an isosceles triangle using altitude and side length, we need to first draw the altitude. The altitude is the segment perpendicular to the base and divides the triangle into two right triangles. The altitude intersects the base at its midpoint.
Step 2: Apply the Pythagorean Theorem to a Right Triangle
Once we have drawn the altitude, we can apply the Pythagorean theorem to one of the right triangles. The theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let’s label the two equal sides of the isosceles triangle as (a) and the base as (b). Also, let’s call the altitude (h). In the right triangle, the hypotenuse is (a), and the other two sides are (h) and (b/2).
Using the Pythagorean theorem, we can write:
a^2 = h^2 + (b/2)^2
Step 3: Solve for the Base
We can rearrange the equation to solve for the base:
(b/2)^2 = a^2 - h^2
b^2 = 4(a^2 - h^2)
b = 2√(a^2 - h^2)
This formula gives us the length of the base (b) of the isosceles triangle using its altitude (h) and one of its equal sides (a).
Finding the Base of an Isosceles Triangle Using the Law of Cosines
When the altitude of an isosceles triangle isn’t readily available, we can turn to the Law of Cosines to determine the base length. This method involves using the relationship between the side lengths and the included angle in a triangle.
In an isosceles triangle, where two sides are equal in length, say ‘a‘ and the base is represented by ‘b,’ we have the following equation:
**c² = a² + b² - 2ab * cos(C)**
where ‘c‘ is the length of the third side, and ‘C‘ is the angle opposite the base.
To find the base ‘b,’ we can rearrange the equation:
**b² = a² + c² - 2ac * cos(C)**
**b = √(a² + c² - 2ac * cos(C))**
Example:
Let’s consider an isosceles triangle with equal sides of 10 cm and an angle between them of 60 degrees. Using the Law of Cosines formula, we can calculate the base length:
“`
b² = 10² + 10² – 2(10)(10) * cos(60)
b² = 200 + 100 – 200 * 0.5
b² = 200 – 100
b² = 100
b = √100
b = 10 cm
Therefore, the base of the isosceles triangle is also 10 cm.
Importance:
The Law of Cosines is a versatile tool for solving a variety of triangle problems, including finding the base of an isosceles triangle. By understanding the relationship between side lengths and angles, we can accurately determine the unknown dimensions of triangles even when the altitude is not immediately known.
Practical Applications of Finding the Base of Isosceles Triangles
Understanding the methods to determine the base of an isosceles triangle extends beyond theoretical knowledge. In various practical applications, this fundamental concept finds significant relevance.
Architecture and Engineering:
When designing structures such as roofs or bridges, architects and engineers often rely on isosceles triangles for their stability. Determining the base length is crucial for ensuring the overall structural integrity.
Surveying and Land Measurement:
In surveying, isosceles triangles are used to establish property boundaries. By measuring the length of the sides and the included angle, surveyors can accurately calculate the base and determine the extent of the land.
Navigation and Geography:
Isosceles triangles play a role in navigation and geography. For instance, sailors use the Law of Cosines to find the distance between two points based on the side lengths and included angle of an isosceles triangle formed by their starting point and two landmarks.
Art and Design:
Artists and designers harness the properties of isosceles triangles to create balanced and visually appealing compositions. The base length influences the overall shape and proportions of a triangle, affecting the overall aesthetic impact of an artwork.
Physics and Engineering:
In physics and engineering, isosceles triangles are commonly encountered in the analysis of forces and moments. Determining the base length is essential for calculating the magnitude and direction of forces acting on a system.
By mastering the techniques for finding the base of isosceles triangles, individuals gain a versatile tool that can be applied across diverse fields, from architecture to navigation and beyond.
Unveiling the Secrets of Isosceles Triangles: A Comprehensive Guide to Determining the Base Length
In the realm of geometry, isosceles triangles hold a special place, characterized by their captivating symmetry. With two equal side lengths, they present an intriguing challenge: determining the length of the base, the side opposite the vertex formed by those equal sides. In this blog, we embark on a captivating journey to unlock the secrets of finding the base of these enigmatic triangles.
Prerequisite Concepts
Before our adventure begins, let us establish a solid understanding of isosceles triangle properties:
- Equal side lengths, denoted as a
- Unequal side length or base, denoted as b
Another important concept is altitude, a perpendicular segment drawn from the vertex opposite the base, creating two right triangles.
Pythagorean Theorem
The Pythagorean theorem comes to our aid when dealing with right triangles. This powerful theorem states that the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. This knowledge will serve as our guiding light in our quest to find the elusive base.
Finding the Base Using Altitude and Side Length
In this method, we imagine drawing an altitude, diving the triangle into two right triangles. Applying the Pythagorean theorem to one of these right triangles gives us:
a² = (b/2)² + h²
where:
- a is the side length
- b is the base length
- h is the altitude
Solving for b, we arrive at:
b = 2√(a² - h²)
Finding the Base Using Two Sides and an Angle
In certain situations, we may know the lengths of the two equal sides (a) and an angle (θ) between them. Here, we employ the Law of Cosines:
b² = a² + a² - 2a²cos(θ)
Solving for b, we get:
b = √(2a² - 2a²cos(θ))
Applications
The ability to find the base of isosceles triangles finds practical applications in various fields:
- Architecture: Designing roofs and bridges with isosceles triangle supports
- Engineering: Calculating forces and moments in structures with isosceles components
- Agriculture: Determining plot sizes and crop yields in isosceles triangular fields
Summary
In this exploration, we have unveiled two powerful methods for finding the base of isosceles triangles. The first method utilizes the Pythagorean theorem, while the second employs the Law of Cosines. Understanding isosceles triangle properties, altitude, and the Pythagorean theorem is paramount in mastering these methods. By equipping ourselves with this knowledge, we unlock the secrets of isosceles triangles, allowing us to confidently navigate their geometric complexities in various real-world applications.