Inverse Relationship Between Period And Frequency In Wave Dynamics

Period and frequency, two fundamental properties of waves, are inversely related: as one increases, the other decreases. Period measures the time for a single oscillation, while frequency denotes the number of oscillations per second. The inverse relationship is evident in the formula f = 1/T, where f is frequency and T is period. For instance, a wave with a period of 0.5 seconds has a frequency of 2 Hz (1/0.5), and conversely, a wave with a frequency of 100 Hz has a period of 0.01 seconds (1/100). Understanding this relationship is crucial in wave dynamics and applications such as acoustics, electromagnetism, and quantum mechanics.

Understanding the Rhythm of Waves: A Tale of Period and Frequency

Waves, like graceful dancers, move across vast bodies of water or propagate through the very fabric of our universe. Understanding their intricate movements requires unraveling the secrets of their period and frequency.

Period and Frequency: The Dance of Time and Oscillation

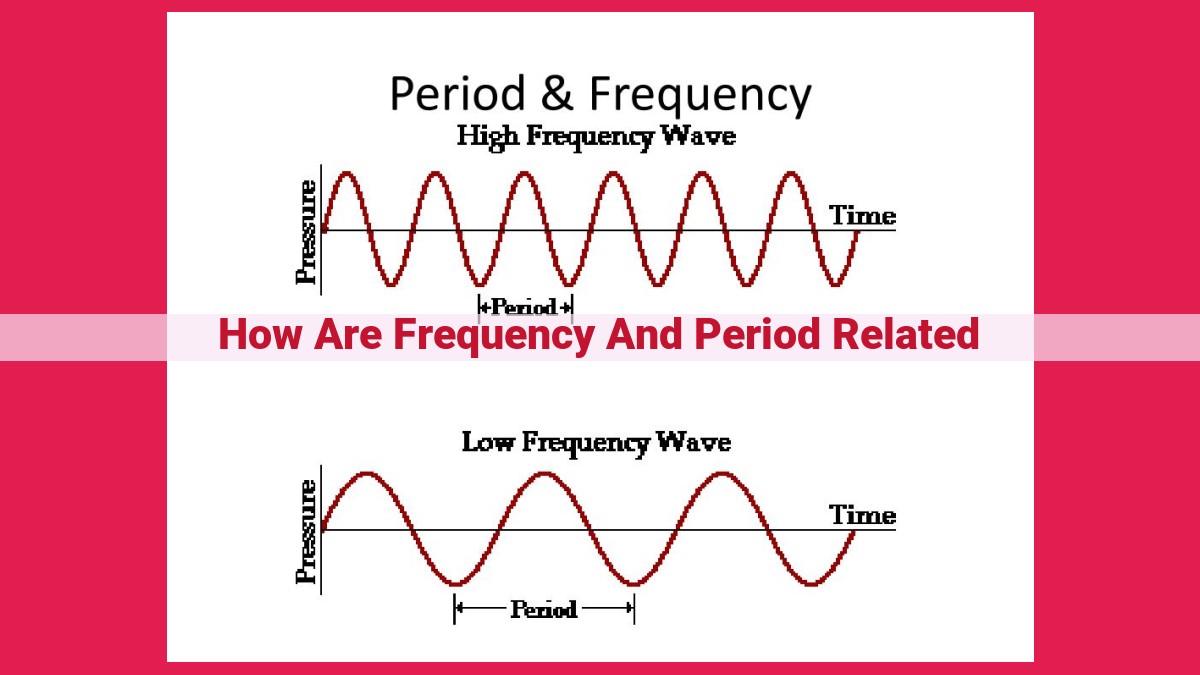
The period of a wave is the time it takes for a single complete oscillation, from its peak to trough and back to peak again. It is like the heartbeat of the wave, marking the rhythm of its movement. On the other hand, frequency measures how often a wave oscillates in one second. It represents the number of complete cycles it performs in a unit of time.

The Inverse Tango: Period’s Decreasing as Frequency Soars

Period and frequency share an inverse relationship, waltzing in opposite directions. As the period of a wave increases, its frequency decreases, and vice versa. This means that longer waves, with longer periods, swing more slowly, while shorter waves, with shorter periods, dance more rapidly.

A Formulaic Connection: Translating Period to Frequency

A simple formula links period and frequency: f = 1/T, where f represents frequency and T represents period. This formula serves as an interpreter, translating between the measures of a wave’s oscillation. If you know the period, you can calculate the frequency, and if you know the frequency, you can determine the period.

Examples in the Wild: Nature’s Symphony of Waves

Nature offers a plethora of examples showcasing the inverse relationship between period and frequency. The gentle lapping of small waves on a calm shore boasts a longer period and lower frequency, while the relentless pound of larger waves crashing against towering cliffs exhibits a shorter period and higher frequency.

Related Concepts: Amplitude, Wavelength, and Velocity

Period and frequency intertwine with other wave characteristics, such as amplitude, wavelength, and velocity. Amplitude refers to the wave’s height, wavelength measures the distance between consecutive peaks or troughs, and velocity determines how fast the wave travels. These concepts, along with period and frequency, form the foundational understanding of wave dynamics.

The inverse relationship between period and frequency holds the key to understanding wave dynamics. It allows us to interpret the rhythmic movements of waves and delve into the intricacies of their behavior. From ocean waves to sound waves, this fundamental concept permeates the world of waves, empowering us to unravel the mysteries of our oscillating universe.

Understanding Period and Frequency: The Rhythm of Waves

Period: The Heartbeat of an Oscillation

Imagine you’re watching a pendulum swing. The period is the time it takes for the pendulum to complete one full oscillation, from its highest point to its lowest and back again. It’s like the heartbeat of the pendulum, a measure of its rhythm.

Frequency: The Number of Beats in a Second

In contrast to period, frequency is the number of oscillations that occur in one second. Think of a strobe light flashing. The frequency is the number of flashes per second. A higher frequency means more flashes, while a lower frequency means fewer.

The Inverse Dance of Period and Frequency

These two quantities are inversely related, like partners in a waltz. As the period increases, the frequency decreases, and vice versa. It’s like a seesaw, where the period goes up when the frequency goes down, and vice versa.

The Inverse Dance of Period and Frequency in Wave Dynamics

Waves, ubiquitous in nature, are characterized by two fundamental properties: period and frequency. Period, the time it takes for a single complete oscillation, is measured in seconds. Frequency, on the other hand, the number of oscillations per second, is expressed in Hertz (Hz).

Their relationship is an intricate inverse dance. As period increases, frequency decreases, and vice versa. Imagine a child on a swing. When the child swings slowly, the time between swings (period) is longer, resulting in a lower frequency. Conversely, when the child swings faster, the period becomes shorter, and the frequency increases.

This inverse relationship can be mathematically expressed by the equation: f = 1/T, where f is frequency and T is period. This formula underscores their reciprocal nature, allowing us to calculate one from the other with ease.

**Unraveling the Intricate Dance of Period and Frequency: Essential Keys to Wave Dynamics**

In the vast expanse of our world, waves hold an enigmatic allure, shaping everything from the gentle ripples of a tranquil pond to the thunderous crash of ocean breakers. At the heart of this mesmerizing dance lies a fundamental relationship: the inverse connection between period and frequency.

Period, simply put, is the duration of a single oscillation, the time it takes for a wave to complete one full cycle. Frequency, on the other hand, measures the number of oscillations that occur in one second. As one increases, the other decreases, like a delicate balancing act.

This inverse relationship is encapsulated in the formula f = 1/T, where f represents frequency and T represents period. This equation empowers us to effortlessly calculate frequency from period (f = 1/T) or vice versa (T = 1/f).

Let’s illuminate this concept with a practical example. Imagine a wave with a period of 2 seconds. Employing the formula, we find its frequency to be 0.5 Hz (1/2). Conversely, a wave with a frequency of 10 Hz would have a period of 0.1 second (1/10).

This inverse relationship plays a crucial role in understanding wave dynamics. Shorter periods correspond to higher frequencies, resulting in waves that appear faster and more energetic. Conversely, longer periods lead to lower frequencies, producing waves that seem slower and gentler.

By grasping the intricacies of period and frequency, we unlock a deeper understanding of the rhythmic pulse of waves. This knowledge forms the foundation for exploring more complex wave phenomena, such as amplitude, wavelength, and velocity. Together, these concepts unravel the tapestry of wave dynamics, enriching our appreciation for the hidden harmonies that govern our physical world.

Understanding the Inverse Relationship between Period and Frequency in Waves

Waves are characterized by their oscillatory motion, repeating over time. Two fundamental properties of waves are period and frequency.

Period is the time it takes for a wave to complete one full oscillation, from its maximum displacement to its next maximum displacement. Frequency is the number of oscillations that occur in one second.

These two properties are inversely related. As the period of a wave increases, its frequency decreases, and vice versa. This inverse relationship is mathematically expressed by the formula:

f = 1/T

where:

• f is frequency
• T is period

This formula demonstrates that if the period is doubled, the frequency is halved, and vice versa.

Practical Examples

To illustrate the inverse relationship, consider the following examples:

• Heart Rate: A person with a high heart rate has a shorter period between beats, resulting in a higher frequency. Conversely, someone with a low heart rate has a longer period and a lower frequency.
• Pendulum: A pendulum with a long string has a longer period and a lower frequency. Conversely, a pendulum with a short string has a shorter period and a higher frequency.
• Sound Waves: A high-pitched sound wave has a shorter period and a higher frequency, while a low-pitched sound wave has a longer period and a lower frequency.

Graphs and Diagrams

The inverse relationship between period and frequency can be visualized using graphs and diagrams.

• Time-Displacement Graph: This graph shows the displacement of a wave over time. A wave with a shorter period will have a steeper graph, indicating faster oscillations.
• Frequency Spectrum: This diagram shows the distribution of frequencies in a signal. A signal with a narrow frequency band has a longer period, while a signal with a wide frequency band has a shorter period.

The inverse relationship between period and frequency is a fundamental property of waves. Understanding this relationship is crucial for analyzing wave dynamics in various fields, including physics, engineering, and music. By grasping the concept of period and frequency, we gain a deeper understanding of the oscillatory nature of waves and their behavior in different contexts.

Understanding the Inverse Relationship between Wave Period and Frequency

In the fascinating realm of physics, waves possess two fundamental characteristics: period and frequency. Period refers to the time it takes for a single complete wave oscillation, while frequency measures the number of oscillations that occur within one second. Understanding the inverse relationship between these two properties is crucial for deciphering the intricate dynamics of waves.

The Inverse Relationship

The period and frequency of a wave exhibit an inverse relationship. This means that as the period increases, the frequency decreases, and vice versa. Mathematically, this relationship is expressed by the formula:

f = 1/T

where:

• f represents the frequency in Hertz (Hz)
• T represents the period in seconds (s)

This formula demonstrates that frequency is inversely proportional to period. If the period increases, the frequency decreases, and if the period decreases, the frequency increases.

Practical Examples

To illustrate this concept, consider a rope tied to a doorknob. When you gently swing the rope, it oscillates at a particular frequency. If you gradually increase the period of the swing by pulling the rope back more slowly, you will notice that the frequency decreases. Similarly, if you shorten the period by increasing the speed of the swing, the frequency increases.

Related Concepts

Period and frequency are closely linked to other wave properties, such as amplitude, wavelength, and velocity.

• Amplitude measures the height or depth of a wave.
• Wavelength is the distance between two consecutive crests or troughs.
• Velocity refers to the speed at which a wave travels.

The period and frequency of a wave influence its wavelength and velocity. Longer periods result in longer wavelengths and slower velocities, while shorter periods lead to shorter wavelengths and faster velocities.