What Is An Integrand? Its Role In Calculus And Integration
An integrand is a function that is integrated to find its antiderivative. It is the input to the integration process, and the output is the antiderivative, which is also known as the integral of the integrand. Indefinite integrals represent antiderivatives, while definite integrals are used to calculate areas under curves. Integrands play a crucial role in calculus, as they provide the foundation for understanding integration and its applications.
Integrands: The Building Blocks of Integration
In the realm of calculus, where functions dance and numbers intertwine, the concept of an integrand takes center stage. An integrand is essentially the function that we integrate. It’s like the raw material from which the magical process of antiderivation produces its enchanting results.
An integrand can be any well-behaved mathematical function. It could be a simple polynomial like x^2 or a more complex trigonometric expression like sin(x). The key is that the integrand must be a continuous function over the interval where we wish to integrate. Just imagine it as the curvy path that we want to find the area under.
The Integral Connection
The relationship between integrands and antiderivatives is a beautiful dance of opposites. An antiderivative is a function whose derivative is the original integrand. Think of the antiderivative as the reverse of the derivative. Just as the derivative tells us how a function changes, the antiderivative tells us how to get back to the original function.
When we integrate an integrand, we’re essentially finding its antiderivative. It’s like retracing our steps along the curvy path, moving from the area under the curve back to the function itself. This process of integration is fundamental in calculus, providing the key to solving countless problems involving rates of change, volumes, and more.
The Connection Between Integrands and Antiderivatives
In the realm of calculus, integrands and antiderivatives dance hand-in-hand, forming an unbreakable bond that weaves the intricate tapestry of integral calculus.
An integrand represents a function whose antiderivative we seek, like a hidden treasure waiting to be unearthed. And what is this coveted treasure? None other than the antiderivative, the function whose derivative is our enigmatic integrand.
Think of an integrand as a footprint, a trace left behind by a wandering function. By retracing its steps through integration, we uncover its antiderivative, the original function that gave rise to this tantalizing trail.
Integration and differentiation, two sides of the same mathematical coin, play a mesmerizing game of hide-and-seek. Integration, the art of uncovering the antiderivative, is the inverse of differentiation, which seeks to find the rate of change.
In the vast landscape of calculus, the relationship between integrands and antiderivatives shines like a beacon, guiding us through the complexities of integral calculus. By understanding this profound connection, we unlock the power to excavate hidden functions and unravel the mysteries of change.
Integration and Integrands
In the realm of calculus, the concept of an integrand intertwines seamlessly with the notion of integration, a mathematical operation that allows us to unlock the mysteries hidden within functions and curves.
An integrand, in essence, is the function or expression being integrated. It represents the infinitesimal change in some variable, such as (x), (y), or (z), and is often denoted by the symbol (f(x)). Integration, on the other hand, is a process that transforms this integrand into a new function, known as an antiderivative.
Imagine a hiker traversing a rugged mountain path. The hiker’s altitude, (f(x)), changes gradually as they ascend the trail. The integrand in this scenario is the hiker’s rate of ascent, (\frac{df}{dx}). By integrating this integrand, we can determine the hiker’s total change in altitude from the start to any point along the path.
Integration thus provides a powerful tool for understanding the behavior of functions. It allows us to calculate areas under curves, volumes of solids, and much more. By breaking down the function into its infinitesimal components, we can piece together a comprehensive picture of its behavior.
Types of Integrals
- Discuss indefinite integrals and definite integrals
Indefinite vs. Definite Integrals: A Calculus Odyssey
In the realm of mathematics, integrals play a crucial role in unlocking the secrets of change and motion. Among these integrals, indefinite integrals and definite integrals stand out as fundamental tools for exploring the intricacies of calculus.
Indefinite Integrals: The Journey of Antiderivatives
Picture an antiderivative as a special function that represents the set of all possible functions whose derivative is the given function. Indefinite integrals embark on a quest to find these antiderivatives, unveiling the secrets of functions.
In simpler terms, if you have a function f(x), the indefinite integral, denoted as ∫f(x)dx, represents the family of functions F(x) such that F'(x) = f(x). This family of functions represents all possible antiderivatives of f(x).
Definite Integrals: Measuring Change with Precision
Unlike their indefinite counterparts, definite integrals focus on a specific interval rather than the entire real line. They seek to precisely calculate the area between a curve and the x-axis or the net change of a function over a specified range.
Definite integrals, represented by ∫[a,b]f(x)dx, measure the area under the curve of the function f(x) between the points x = a and x = b. They provide a quantitative understanding of the change or accumulation that occurs within that specific interval.
Indefinite and definite integrals are indispensable tools in the calculus toolkit. They empower us to explore the intricate world of change, unlocking the mysteries of functions and quantifying the evolution of quantities over time.
Understanding these integral types is essential for unlocking the full potential of calculus. They serve as gateways to deeper exploration, enabling us to solve complex problems and gain insights into the dynamic nature of our world.
Indefinite Integrals and Antiderivatives: Unlocking the Secrets of Functions
In the realm of calculus, we encounter the intriguing concept of the integral. An integral, represented by a stylized elongated S, is essentially a mathematical operation that reverses the process of differentiation. In this article, we will delve into the world of indefinite integrals and explore their intimate connection with antiderivatives.
Indefinite Integrals: A Journey of Anticipation
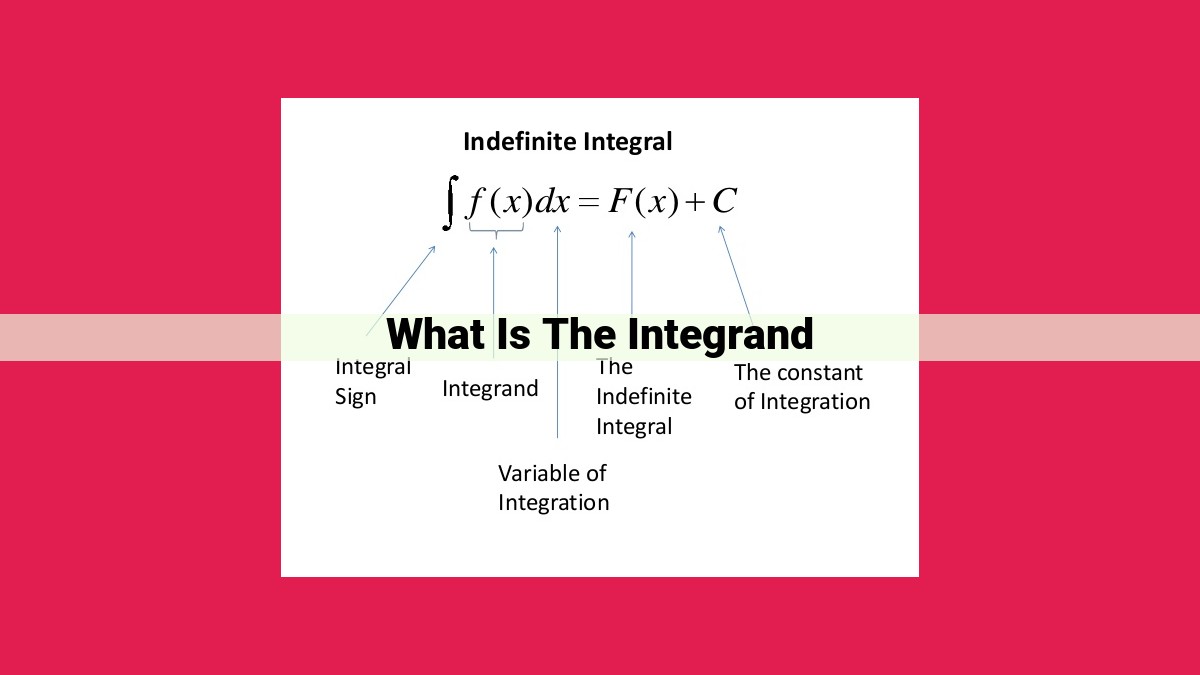
An indefinite integral is an integral that does not specify the limits of integration. We denote it using an elongated S with a small “c” next to it, known as the constant of integration:
∫f(x) dx = F(x) + C
Here, f(x) is the integrand, and F(x) is the antiderivative of f(x). An antiderivative is a function whose derivative is the original function. This relationship between integrals and antiderivatives is a fundamental concept in calculus.
The Antiderivative Connection: A Path to Recovery
An antiderivative is a function that, when differentiated, gives us back the original function. For example, if f(x) = x^2, then its antiderivative is F(x) = x^3/3 + C, where C is an arbitrary constant. This means that the indefinite integral of x^2 is:
∫x^2 dx = x^3/3 + C
The constant of integration C arises because there are infinitely many functions whose derivatives are the same. By adding C, we account for this family of antiderivatives.
The Role of Indefinite Integrals: A Bridge to Understanding
Indefinite integrals play a crucial role in calculus. They allow us to:
- Find the area under a curve
- Calculate volumes of solids of revolution
- Model physical processes involving rates of change
Indefinite Integrals in Context: A Real-World Example
Let’s say you want to find the area under the curve y = x^2 between x = 0 and x = 2. The indefinite integral of x^2 is F(x) = x^3/3 + C. To find the area, we evaluate the indefinite integral at the given limits:
Area = ∫[0, 2] x^2 dx = [x^3/3 + C] from 0 to 2 = 8/3 sq. units
Indefinite integrals, hand in hand with antiderivatives, form the cornerstone of integral calculus. They provide a powerful tool for understanding and manipulating functions, opening doors to a wide range of applications in mathematics, physics, and engineering.
Definite Integrals and Areas
- Define definite integrals and explain how they are used to find areas under curves
Definite Integrals and Areas: Unlocking the Secrets Under Curves
In the realm of calculus, where functions dance and numbers unravel, we encounter a fascinating concept known as definite integrals. These mathematical tools hold the key to unlocking the hidden areas beneath the curves that shape our world.
A definite integral is a special type of integral that calculates the area between a curve and the x-axis over a specific interval. Unlike its indefinite counterpart, a definite integral has both an upper and a lower limit, denoted by a and b, respectively.
Imagine a graph where a curve y = f(x) gracefully arches above the x-axis. Between the x-values a and b, the definite integral of f(x) represents the total area enclosed by the curve, the x-axis, and the vertical lines x = a and x = b.
Visualize it: The area under the curve is like a slice of pizza. The definite integral is the process of cutting that slice into infinitely thin strips and adding up their areas to get the entire pizza’s area.
Formula and Notation:
The formula for a definite integral of f(x) over the interval [a, b] is:
∫[a, b] f(x) dx
Example:
Let’s find the area under the curve y = x^2 between x = 0 and x = 2. The definite integral is:
∫[0, 2] x^2 dx = [x^3 / 3] from 0 to 2 = 8/3
The result, 8/3, represents the total area under the curve y = x^2 from x = 0 to x = 2. This area can be interpreted as the area of a triangle or a parabola, depending on the context.
Definite integrals find widespread applications in various fields, including engineering, physics, and economics. They help us calculate volumes, work done by forces, probabilities, and many more. By understanding and utilizing the power of definite integrals, we can unlock the secrets hidden beneath the curves that shape our surroundings.
The Intriguing World of Integrands: A Journey Through Calculus
What is an Integrand?
In the realm of mathematics, an integrand is a mathematical expression or function that lies at the heart of integral calculus. It represents the function under the integral sign. Imagine it as the building block of integrals, the essential ingredient that gives integrals their shape and purpose.
The Connection to Antiderivatives
Integrands and antiderivatives are two sides of the same mathematical coin. The antiderivative of an integrand is the function whose derivative is equal to the integrand. This intimate relationship allows us to find antiderivatives by integrating integrands. Integration, in essence, is the process of discovering the antiderivative of a given integrand.
Integration and Integrands: A Dance of Unlocking Functions
Integration is the mathematical operation that transforms an integrand into its antiderivative. Just as a derivative tells us the rate of change, integration reveals the original function from which the integrand was derived. Integrands play a pivotal role in integration, providing the necessary information to uncover the hidden function.
Types of Integrals: Uncovering Shapes and Areas
Integrals fall into two primary categories: indefinite integrals and definite integrals. Indefinite integrals yield a family of antiderivatives, representing all possible functions that have the given integrand as their derivative. Definite integrals, on the other hand, calculate the area under the curve defined by the integrand over a specific interval.
Indefinite Integrals and Antiderivatives: A Symbiotic Relationship
Indefinite integrals serve as a powerful tool for finding antiderivatives, the functions who “bring integrals to life.” The indefinite integral of an integrand is an expression that represents all possible antiderivatives. This concept forms the cornerstone of solving differential equations and modeling real-world phenomena.
Definite Integrals and Areas: Quantifying the Unseen
Definite integrals measure the area under the curve of a function over a given interval. They provide a quantitative understanding of the shape and extent of the region bounded by the curve. Definite integrals are particularly useful in fields such as physics, engineering, and economics, where they help quantify physical quantities and model system behavior.
Example: Integrating x^2
To illustrate the process of finding an indefinite integral, let’s consider the integrand x^2. Integrating this expression involves the Power Rule, which states that the integral of x^n is x^(n+1)/(n+1). Applying this rule to x^2, we obtain the indefinite integral:
∫x^2 dx = x^3/3 + C
where C is an arbitrary constant representing the family of antiderivatives.
Integrands are the cornerstones of integral calculus, playing a crucial role in uncovering antiderivatives, calculating areas, and modeling real-world phenomena. Their importance extends far beyond the walls of academia, finding applications in diverse fields, from physics and engineering to economics and finance. By understanding integrands, we unlock the power of integrals and gain a deeper appreciation for the intricate tapestry of calculus.