Infinite Discontinuities In Functions: Identifying Asymptotes And Types For Optimal Function Behavior

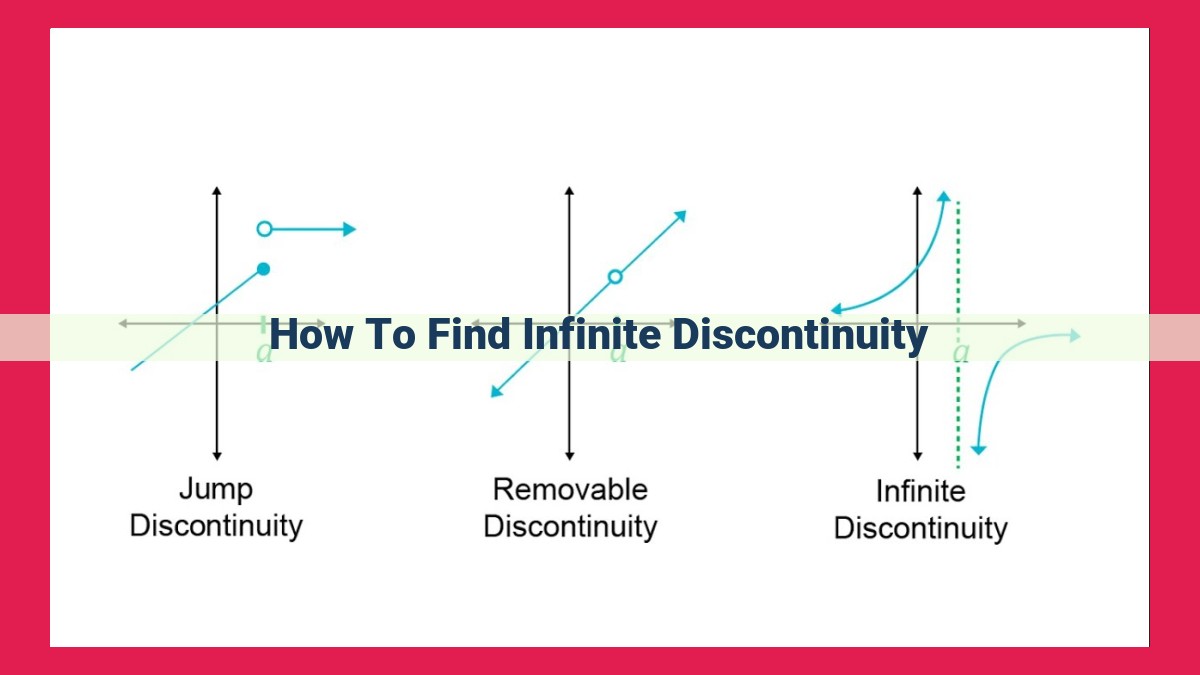
To find infinite discontinuity, identify functions where the limit at the point of discontinuity is infinity. This can be indicated by vertical asymptotes in the graph. Infinite discontinuities fall into two types: removable, where the discontinuity can be eliminated by redefining the function, and non-removable, where it cannot be removed. Removable discontinuities create “holes” in the graph, while non-removable discontinuities result in jumps or breaks in the function’s behavior.

Discontinuities: A Tale of Interrupted Functions

In the realm of mathematical functions, discontinuities arise when the function’s values abruptly change at specific points. These disruptions can lead to fascinating behaviors and insights into the nature of the function.

Types of Discontinuities:

Infinite Discontinuities: These occur when a function’s value approaches infinity at a particular point. Like celestial bodies zipping past the horizon, they leave behind a trail of vertical asymptotes, imaginary lines where the function’s value cannot be defined.

• Removable Discontinuities: These infinitesimal interruptions can be smoothed out by redefining the function at the discontinuous point. They are the mathematical equivalent of a tiny pothole that can be filled to restore the function’s continuous flow.

• Non-Removable Discontinuities: These persist even after attempting to redefine the function. They are the stubborn roadblocks that refuse to budge, creating permanent fissures in the function’s graph.

Infinite Discontinuities: When Functions Go to Infinity

In the realm of mathematics, discontinuities disrupt the otherwise smooth flow of a function’s graph. Among these interruptions, infinite discontinuities stand out as points where the function’s value becomes unbounded, soaring towards infinity.

Conditions for an Infinite Discontinuity

An infinite discontinuity arises when a function approaches infinity as the input variable approaches a specific value. This occurs when the denominator of a fraction becomes zero while the numerator remains nonzero. The resulting division yields an undefined expression, represented as $\infty$.

Examples of Functions with Infinite Discontinuities

Consider the function $f(x) = \frac{1}{x-2}$. At $x=2$, the denominator vanishes, leaving us with an infinite discontinuity. As $x$ gets closer and closer to 2, the value of $f(x)$ grows larger and larger, either positively or negatively, depending on the sign of the numerator.

Another example is $g(x) = \tan x$ at $x = \frac{\pi}{2}$. In this case, the tangent function becomes undefined as the cosine of $x$ approaches zero, resulting in an infinite discontinuity.

Behavior of Infinite Discontinuities

Functions with infinite discontinuities exhibit a characteristic behavior when graphed. They often have vertical asymptotes at the discontinuity points. A vertical asymptote is a vertical line that the graph approaches but never touches. It indicates that the function’s value is undefined at that point.

The graph of a function with an infinite discontinuity may also have a hole at the discontinuity point. A hole represents a point where the function is undefined but can be redefined to make the function continuous.

Understanding infinite discontinuities is crucial for analyzing the behavior of functions and making informed decisions about mathematical models. These discontinuities provide valuable insights into the limits and singularities that shape the mathematical landscape.

Removable Discontinuities: Smoothing out the Rough Edges

In the realm of mathematics, discontinuities can be like unexpected roadblocks on a function’s smooth journey. But what if these roadblocks could be removed, paving the way for a seamless experience? Enter removable discontinuities!

Removable Discontinuities: A Definition

A removable discontinuity occurs when a function’s graph has a hole that could be filled by redefining the function at that point. Unlike infinite discontinuities, which cause the graph to jump or soar to infinity, removable discontinuities are less dramatic.

Methods for Removing Removable Discontinuities

To remove a removable discontinuity, we simply need to redefine the function at the point where it’s discontinuous. This can be done in several ways:

• Factorization and Cancellation: If the discontinuity is caused by a factor in the denominator that can be canceled out, we can factor the expression and simplify it.
• Redefining the Function: In some cases, we can redefine the function at the point of discontinuity to make it continuous. For instance, we can assign a specific value to the function at that point.

Example: Smoothing out a Removable Discontinuity

Consider the function f(x) = (x-2) / (x-1). This function has a removable discontinuity at x = 1 because the denominator cancels out at that point.

To remove the discontinuity, we can factor the numerator and cancel out the common factor:

f(x) = (x-2) / (x-1) = 1

By redefining the function as f(1) = 1, we have eliminated the removable discontinuity and created a smooth, continuous graph.

Removable discontinuities are less severe interruptions in a function’s graph. By understanding the concept and employing techniques like factorization and redefinition, we can smooth out these bumps and ensure a continuous journey. These refined functions allow us to better analyze and interpret the behavior of our mathematical equations.

Non-Removable Discontinuities: An Exploration of Unbridgeable Gaps

In the realm of functions, discontinuities are intriguing anomalies that disrupt the smooth flow of their graphs. Non-removable discontinuities, in particular, stand out as persistent obstacles that cannot be rectified by mere mathematical tweaks.

Unlike removable discontinuities, which can be magically erased by redefining the function at the problematic point, non-removable discontinuities are stubborn entities that refuse to budge. They arise when a function experiences a fundamental breakdown in its structure, leaving behind an unfillable chasm in its domain.

One common culprit behind non-removable discontinuities is the presence of an infinite limit. When a function approaches infinity (either positively or negatively) as it nears a particular point, a vertical asymptote appears to mark the boundary of its domain. This asymptote represents the insurmountable barrier that prevents the function from crossing the gap and achieving continuity.

For example, consider the function (f(x) = 1 / (x – 2)). As (x) approaches 2, the function’s value becomes infinitely large, creating a vertical asymptote at (x = 2). No matter how we tinker with the function’s definition at that point, the discontinuity remains unmovable.

Another breed of non-removable discontinuities stems from oscillations. These functions behave like restless travelers, bouncing back and forth across a particular point without ever settling down on either side. Take, for instance, the function (f(x) = sin(1 / x)). As (x) approaches 0, the function oscillates wildly between -1 and 1, leaving a gaping hole in its graph.

Non-removable discontinuities are not mere curiosities; they have profound implications for the function’s behavior. They can dictate the function’s domain, affect its differentiability, and even cause it to have multiple branches. Understanding these discontinuities is crucial for fully comprehending the landscape of a function and its mathematical idiosyncrasies.

Understanding Holes in the Graph: A Guide to Removable Discontinuities

Introduction:
In the realm of mathematics, discontinuities are points where functions behave erratically, causing gaps or jumps in their graphs. One type of discontinuity that often arises is removable discontinuities, also known as holes in the graph. In this article, we’ll explore the concept of holes in the graph, their relationship to removable discontinuities, and how to identify and interpret them.

What are Holes in the Graph?
Holes in the graph refer to points where a function is undefined, but the limit of the function as it approaches that point exists. This means that if we were to connect the two sections of the graph on either side of the hole, the resulting graph would be continuous.

Relationship to Removable Discontinuities:
Removable discontinuities and holes in the graph are two sides of the same coin. When we have a removable discontinuity, it means that the function is undefined at a particular point, but we can redefine the function at that point to make it continuous. This redefinition fills the hole in the graph, making the function continuous across its entire domain.

Identifying Holes in the Graph:
To identify holes in the graph, we can look for points where the function is undefined but the limit of the function as it approaches that point exists. Graphically, this appears as a small gap or discontinuity in the graph.

Interpreting Holes in the Graph:
The presence of a hole in the graph suggests that there is a value that the function should have at that point, but it is missing. This missing value can be due to various reasons, such as the function being defined only for certain intervals or the function having a discontinuity that can be removed by redefining the function.

Conclusion:
Holes in the graph are an important concept in understanding the behavior of functions. They represent removable discontinuities where the function can be redefined to make it continuous. By identifying and interpreting holes in the graph, we gain a deeper understanding of the function’s behavior.

Jump Discontinuities

• Explain what jump discontinuities are and how they differ from other types of discontinuities.
• Provide examples of functions with jump discontinuities and discuss their characteristics.

Jump Discontinuities: A Tale of Sudden Breaks

In the realm of functions, discontinuities are like bumps in the road, disrupting the smooth flow of their graphs. Among these disruptions, jump discontinuities stand out as abrupt leaps from one point to another. Unlike their gradual counterparts, they occur when a function’s value changes instantly at a specific point.

Consider the graph of the function f(x) = x – 1, a linear function with a continuous graph. Now imagine the following scenario: we add a single point x = 2 with a different function value of f(2) = 3. Suddenly, the graph jumps from the point (2, 1) to (2, 3). This abrupt transition is a classic example of a jump discontinuity.

Jump discontinuities can arise from various mathematical operations. For instance, the function f(x) = 1/(x – 2) has a jump discontinuity at x = 2 because the denominator becomes zero at that point, creating an infinite discontinuity. However, when we allow the graph to extend beyond x = 2, we observe two separate branches that meet at that point, resulting in a jump discontinuity.

Another common source of jump discontinuities is piecewise functions, which define different formulas for different intervals of the input. For example, the function f(x) = {x + 1 if x < 0, -x if x ≥ 0} switches between two linear functions at x = 0, creating a jump discontinuity at that point.

Jump discontinuities differ from other types of discontinuities in several ways. Unlike infinite discontinuities, which approach infinity, jump discontinuities involve a finite change in value. Furthermore, while removable discontinuities can be made continuous by redefining the function at that point, jump discontinuities cannot be removed without fundamentally altering the function’s behavior.

In conclusion, jump discontinuities are distinct disruptions in the continuity of a function’s graph. They occur when the function’s value changes instantly at a specific point, resulting in an abrupt leap. Understanding these discontinuities is crucial for accurately analyzing and interpreting the behavior of functions in the real world.