Understand Moment Of Inertia: Key To Rotational Motion

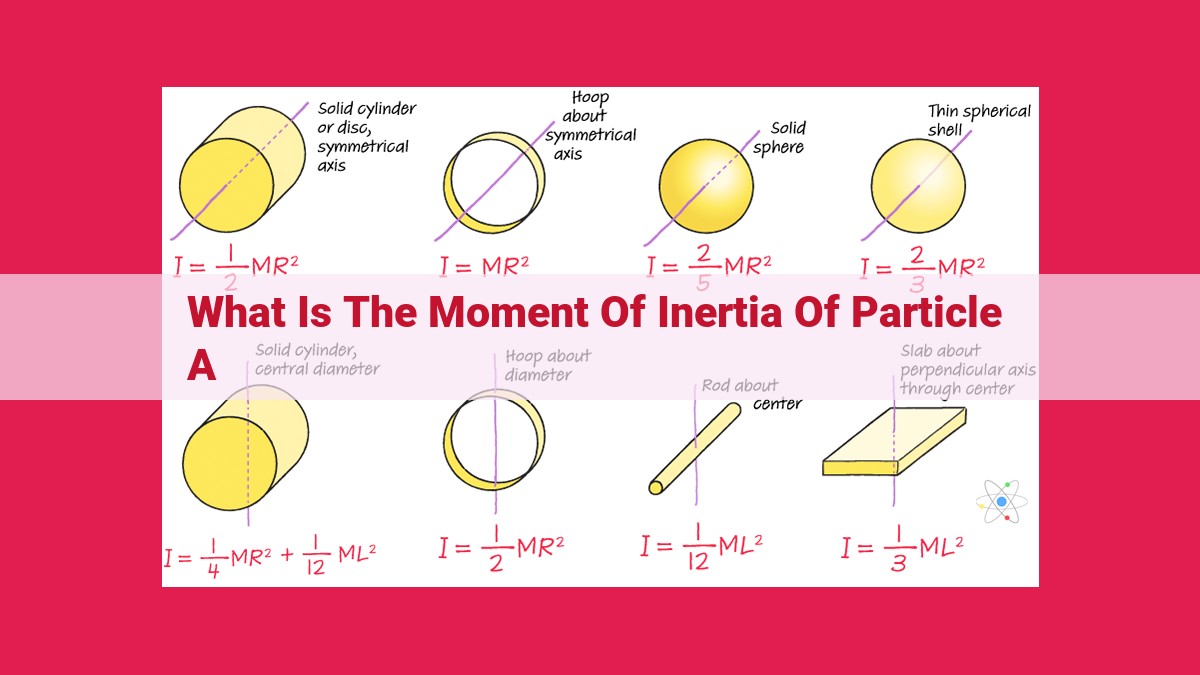
The moment of inertia of particle A refers to its resistance to rotational acceleration around an axis. It is a scalar quantity determined by the particle’s mass and its distance from the axis of rotation. The higher the mass or the greater the distance, the higher the moment of inertia. It plays a crucial role in understanding rotational motion, as it determines the particle’s angular velocity and rotational kinetic energy.

Moment of Inertia: A Key Concept in Understanding Rotational Motion

Imagine a spinning top or a rotating planet. These objects appear to resist changes in their rotational motion, a phenomenon that can be attributed to a fundamental property called moment of inertia. Moment of inertia is a measure of an object’s resistance to rotational acceleration. It plays a pivotal role in understanding how objects behave during rotational motion.

Moment of inertia is analogous to mass in linear motion. While mass determines an object’s resistance to linear acceleration, moment of inertia quantifies an object’s resistance to rotational acceleration. The larger an object’s moment of inertia, the more difficult it is to change its rotational motion. This concept is crucial for analyzing the motion of rotating objects in various fields, such as physics, engineering, and astronomy.

Moment of Inertia: Understanding a Particle’s Resistance to Rotational Motion

Moment of inertia, often denoted by the symbol I, is a crucial concept in understanding the rotational motion of objects. Essentially, it measures how difficult it is for an object to rotate around an axis. Imagine a child on a merry-go-round; the more massive the child (heavier mass) and the farther away they sit from the center (greater distance from the axis), the harder it is to spin the merry-go-round.

Mass and Moment of Inertia

Mass plays a significant role in determining the moment of inertia. The heavier the particle, the greater its moment of inertia. This is because mass represents the amount of matter in the particle, and more matter means more resistance to rotation.

Distance from the Axis

The distance of the particle from the axis of rotation also has a profound impact on its moment of inertia. The farther the particle is from the axis, the higher its moment of inertia. Picture a ballerina spinning on the spot; when she extends her arms, her moment of inertia increases because her mass is now distributed farther away from the axis.

Mathematical Formula

The relationship between mass, distance, and moment of inertia is mathematically expressed as:

I = m x r^2

Where:

• I is the moment of inertia
• m is the mass of the particle
• r is the distance from the axis of rotation

This formula highlights that moment of inertia is proportional to both mass and the square of the distance from the axis.

Rotational Motion and Moment of Inertia

The Dance of Rotation and Resistance

In the realm of physics, rotational motion captivates us with its mesmerizing dance of objects spinning and twirling. Just as mass plays a pivotal role in linear motion, moment of inertia emerges as the governing force in rotational motion, determining an object’s defiance against angular acceleration.

Angular Velocity and Moment of Inertia: A Delicate Balance

Picture a ballerina pirouetting gracefully; her outstretched arms increase her moment of inertia. This increased inertia makes her more resistant to changes in her angular velocity. Similarly, in physics, a particle with a greater moment of inertia resists rotational acceleration more resolutely.

Torque: The Catalyst of Rotation

Torque emerges as the driving force behind rotational motion. Think of a doorknob you turn; the force you apply creates a torque, causing the door to rotate. The greater the torque acting on a particle, the greater its resistance to rotational acceleration, as dictated by its moment of inertia.

Practical Applications: From Spinning Tops to Celestial Orbits

The concept of moment of inertia extends far beyond theoretical explorations. It governs the rotational motion of a wide array of objects, from spinning tops mesmerizing children to the majestic dance of planets around the sun. Engineers harness it to design efficient flywheels for energy storage, while astronomers rely on it to calculate the rotational periods of celestial bodies.

By understanding the interplay between rotational motion and moment of inertia, we unlock the secrets of objects in motion, from the smallest particles to the grandest cosmic bodies.

The Moment of Inertia: Unlocking the Secrets of Rotational Motion

Imagine a spinning wheel, its motion fluid and graceful. Or a pendulum swinging back and forth, its rhythmic sway a testament to the forces acting upon it. These seemingly simple objects hold a hidden secret: the moment of inertia, a measure that quantifies their resistance to changes in rotational motion.

The Essence of Moment of Inertia

Simply put, the moment of inertia, denoted by the symbol I, is a measure of an object’s tendency to resist rotational acceleration. Just as mass gauges an object’s resistance to linear acceleration, moment of inertia captures its “rotational inertia.”

Moment of Inertia and Its Factors

The moment of inertia is not an inherent property but depends on two key factors:

• Mass: The more massive an object is, the greater its moment of inertia. It takes more force to accelerate a heavier object rotationally.

• Distance from the Axis: The distance of the object’s mass from the axis of rotation plays a crucial role. Mass located farther from the axis contributes more to the moment of inertia.

The Mathematical Formula for Moment of Inertia

For a single particle rotating about a fixed axis, the moment of inertia is expressed by the equation:

I = m x r^2

where:

• I is the moment of inertia
• m is the mass of the particle
• r is the distance from the particle to the axis of rotation

Moment of Inertia and Rotational Motion

The moment of inertia is critical in determining the rotational motion of an object. It influences the object’s resistance to changes in its angular velocity, which measures how fast the object is rotating. Objects with a larger moment of inertia are more difficult to accelerate rotationally.

Applications of Moment of Inertia

The moment of inertia finds numerous applications in physics, engineering, and everyday life:

• Analyzing Rotational Motion: Engineers use moment of inertia to design rotating machinery, such as wheels, gears, and flywheels, to optimize their performance.

• Calculating Rotational Kinetic Energy: The rotational kinetic energy of an object is directly proportional to its moment of inertia and angular velocity. This knowledge is essential in fields like sports biomechanics and machine design.

• Other Practical Applications: Moment of inertia also plays a role in calculating the stability of objects, the oscillation of pendulums, and the dynamics of celestial bodies like planets orbiting the sun.