Identifying Linear Equations: A Guide To Distinguishing Linearity

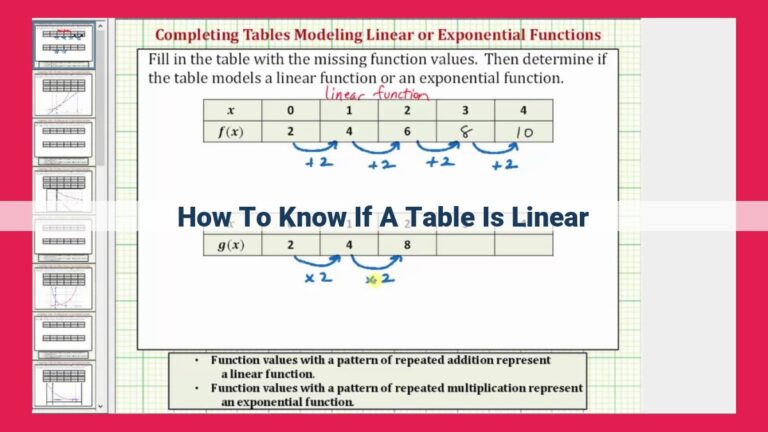
To determine if an equation is linear, analyze its form. A linear equation is represented by y = mx + b, where m is the slope and b is the y-intercept. If an equation matches this form, it is linear. Conversely, if it deviates from this form, it is non-linear.

• Explain the significance of understanding linear equations in mathematics and real-world applications.

Unveiling the enigma of linearity is akin to embarking on an enchanting journey, where the comprehension of linear equations unveils a tapestry of mathematical elegance and real-world practicality. Understanding these equations empowers us to navigate the intricate world of straight lines, unraveling their hidden secrets and unlocking their transformative power. From predicting the trajectory of a flying projectile to modeling economic growth, linear equations serve as a ubiquitous tool, orchestrating the symphony of science and everyday life.

The Importance of Linearity

Imagine a quaint cottage by the tranquil shores of a picturesque lake. As the setting sun casts an ethereal glow upon the cerulean waters, a young maiden plucks a willow leaf and gently drops it into the serene depths. Ripples emanate from the point of impact, spreading outward in perfect concentric circles. This mesmerizing display of nature epitomizes linearity, a fundamental concept that governs the behavior of countless phenomena in the realm of both mathematics and real-world applications.

By understanding linear equations, we gain the ability to describe and predict patterns in a myriad of contexts. In the world of science and engineering, they model the motion of objects, predict the trajectory of projectiles, and design structures that can withstand the test of time. In the realm of economics, they help us analyze market trends, forecast demand, and make informed decisions.

Understanding Slope: Embarking on a Journey of Steepness and Direction

In the realm of mathematics, where intricate equations unravel the mysteries of our world, the concept of slope emerges as a guiding light, illuminating the character of lines. Slope, akin to a line’s fingerprint, captures its distinctive steepness and direction. Join us on an adventure as we explore the intricacies of slope, unraveling its significance and embracing its power as a mathematical explorer.

Unveiling Slope: The Compass of Steepness and Incline

Imagine a line traversing a coordinate plane, dancing across its grid. Slope serves as the compass that measures the line’s inclination, revealing how steeply it ascends or descends. A line with a positive slope soars upward, like a bird taking flight. Conversely, a negative slope sends the line plunging downward, like a waterfall cascading over a cliff’s edge. The greater the absolute value of the slope, the more pronounced the line’s steepness.

Allied Concepts: Gradient, Rate of Change, and Steepness

Gradient, a synonymous term for slope, captures the essence of the line’s ascent or descent. It represents the rate of change in the line’s y-coordinate for every unit change in its x-coordinate. A positive gradient signifies an upward trajectory, while a negative gradient indicates a downward path.

Another close companion of slope is steepness. Steepness quantifies the line’s inclination, revealing its angle of ascent or descent. The steeper the line, the more dramatic its rise or fall. Conversely, a less steep line exhibits a gentler incline. Understanding these allied concepts enhances our grasp of slope and its multifaceted nature.

Exploring Related Illustrations

• Hillside Trek: Picture a rugged hiking trail winding up a verdant hillside. The trail’s steepness, determined by its slope, challenges hikers as they ascend. A steeper trail demands greater effort, while a gentler slope allows for a more relaxed climb.
• Water Flow: Observe a swiftly flowing river, its cascading waters forming a steep waterfall. The waterfall’s slope mirrors the river’s rapid descent, while a meandering stream exhibits a more gradual slope, reflecting its leisurely pace.
• Financial Growth: Track the trajectory of a stock’s price over time. The stock’s slope reveals its rate of growth or decline, providing insights into its performance and potential.

Identifying the Y-Intercept: Determining the Line’s Origin

• Definition of the y-intercept and its representation as the point where the line crosses the y-axis.
• Related concepts: initial value and starting point.

Identifying the Y-Intercept: The Line’s Point of Origin

In the world of mathematics, understanding the intricacies of linear equations is as crucial as finding a map in an uncharted territory. And just like in geography, there are significant landmarks in the land of linear equations, and one of them is the y-intercept.

The y-intercept is the point where a line kisses the y-axis. It’s the line’s entry point into the two-dimensional world we call a graph. Think of it as the starting line of a race where the y-axis is the starting gate.

The y-intercept is often denoted by the letter b, and it represents the initial value of the line. It’s the value of the y-coordinate when the x-coordinate is zero. In other words, it tells us where the line begins on the y-axis.

For example, consider the linear equation y = 2x + 3. The y-intercept of this line is 3. This means that when x is 0, y is 3. So, the line starts at the point (0, 3) on the graph.

The y-intercept is an important characteristic of a linear equation because it gives us a way to quickly visualize and understand the line’s behavior. It’s like a sneak peek into the line’s personality, revealing its starting point and direction.

So, the next time you encounter a linear equation, don’t forget to pay attention to its y-intercept. It’s the key to unlocking the line’s secrets and understanding its journey through the graph.

Recognizing Linear Equations: Unveiling the Beauty of Straight Lines

In the realm of mathematics, equations serve as the language that describes the world around us. Among the vast tapestry of equations, linear equations hold a captivating simplicity that reveals the essence of straight lines.

A linear equation is an algebraic expression that represents a straight line on a graph. It is expressed in the form y = mx + b, where:

• y is the dependent variable, which represents the output of the equation.
• x is the independent variable, which represents the input to the equation.
• m is the slope of the line, determining its steepness and direction.
• b is the y-intercept, indicating where the line intersects the y-axis (when x = 0).

The beauty of linear equations lies in their ability to describe simple yet fundamental relationships. They are found everywhere, from the trajectory of a thrown ball to the growth of a plant. By recognizing linear equations, we gain a powerful tool for understanding and predicting the world around us.

To identify a linear equation, look for expressions that fit the y = mx + b format. First, check if the equation is a straight line by analyzing the exponent of x. In a linear equation, x has an exponent of 1. If it has any other exponent, the equation is not linear.

Furthermore, remember that m determines the slope and direction of the line. A positive slope indicates an upward slope, while a negative slope indicates a downward slope. The y-intercept (b) represents the point where the line intersects the y-axis.

Mastering the art of recognizing linear equations empowers you to unlock a treasure trove of mathematical applications and real-world scenarios. Embrace their simplicity and elegance, and you will find yourself navigating the world of mathematics with greater confidence and clarity.

Understanding Constants: The Unchanging Values in Equations

In the realm of mathematics, constants are like steadfast beacons, unyielding in their stability amidst the ever-changing landscape of variables. They represent values that remain constant, unperturbed by the fluctuations of their companions.

What Are Constants?

Simply put, a constant is a numerical value that does not change within a given equation. It is akin to a steadfast rock, unwavering in its presence and value. Unlike variables, which can assume different values depending on the context, constants remain immutable, their essence unyielding.

Importance of Constants

In the symphony of mathematical equations, constants play a pivotal role, providing a point of reference amidst the flux. They serve as the anchors that keep the equation grounded, ensuring that the relationship between variables remains consistent.

Identifying Constants

Spotting constants is a straightforward task. They typically appear as numbers that are not prefixed by a variable. These numerical entities stand alone, independent of the ever-changing variables that dance around them.

Examples of Constants

In the following equation, y = 2x + 5, the constant is 5, an unwavering value that remains unchanged regardless of the value of x.

Distinguishing Constants from Variables

In the world of equations, constants are the steady companions of variables. Variables, on the other hand, are the dynamic elements, changing their values as the equation evolves. Constants provide a sense of stability and predictability, while variables introduce an element of fluidity.

Defining Variables: X and Y, the Independent and Dependent

In the realm of mathematics, variables serve as enigmatic symbols, representing unknown quantities that dance within equations. Among these variables, none hold more sway than the illustrious X and Y, the independent and dependent variables.

X: The Independent Variable (Input)

Imagine a mischievous jester preparing to juggle a rainbow of balls. The jester’s mischievous intent? To control the number of balls he juggles at once, a decision represented by X, the independent variable. In this scenario, X reigns supreme, dictating the input or cause that sets the equation in motion.

Y: The Dependent Variable (Output)

As the balls soar through the air, their trajectory and outcome are determined by the jester’s input. The number of balls that gracefully land in his outstretched hands, represented by Y, the dependent variable, is merely an effect of his original decision. Y dances at the whims of X, the cause and effect harmoniously intertwined.

It is important to note that variables in mathematics behave like chameleons, changing their roles based on the context. The same variable may assume the guise of an independent variable in one equation and a dependent variable in another, much like the proverbial chameleon’s ability to blend seamlessly into its surroundings.

Determining Linearity: Examining the Equation’s Form

The standard form of a linear equation is y = mx + b, where m represents the slope and b represents the y-intercept. This equation describes a straight line on a graph. The slope determines the steepness of the line, while the y-intercept determines where the line crosses the y-axis.

Non-linear equations, on the other hand, deviate from this standard form. They may contain terms such as x^2, x^3, sin(x), or log(x), which make the graph of the equation non-linear. These equations often describe curves or other non-straight lines.

To determine whether an equation is linear, you can check if it can be expressed in the standard form y = mx + b. If it can, then the equation is linear. If it cannot, then the equation is non-linear.

Here are some examples:

• Linear Equation (y = mx + b): y = 2x – 5
• Non-Linear Equation: y = x^2 + 3

The first equation is linear because it can be written in the standard form y = 2x + (-5). The second equation is non-linear because it contains the term x^2.