Optimized Seo Title:identify Polynomial Functions: Characteristics, Properties, And Examples

A polynomial function is a function that can be written as a sum of terms, each with a non-negative integer exponent. Polynomial functions have a degree, coefficients, and a constant term. To identify a polynomial function, check the exponents of the terms; they must be non-negative integers. Common examples include linear functions (degree 1), quadratic functions (degree 2), and cubic functions (degree 3). Polynomial functions have a domain of all real numbers and a range that depends on the degree. They can have intercepts on the x-axis and y-axis. Non-polynomial functions, such as rational functions, exponential functions, and trigonometric functions, do not meet the properties of polynomial functions.

What are Polynomial Functions?

In the realm of mathematics, where functions reign supreme, we encounter a particular type known as polynomial functions. These functions are the embodiment of elegance and order, defined by their unique characteristic of being expressed as a sum of terms, each adorned with a non-negative integer exponent. In other words, they are functions that can be written as:

f(x) = a_n * x^n + a_{n-1} * x^(n-1) + ... + a_1 * x + a_0

where n is a non-negative integer called the degree of the polynomial, a_n is the leading coefficient, and a_0 is the constant term.

Properties of Polynomial Functions: Understanding the Language of Equations

In the realm of mathematics, polynomial functions reign supreme. They are mathematical expressions that, like a symphony of terms, paint a picture of a function’s behavior. But what sets them apart? Understanding their intricate properties is the key to unlocking their power.

Degree: The Height of a Polynomial

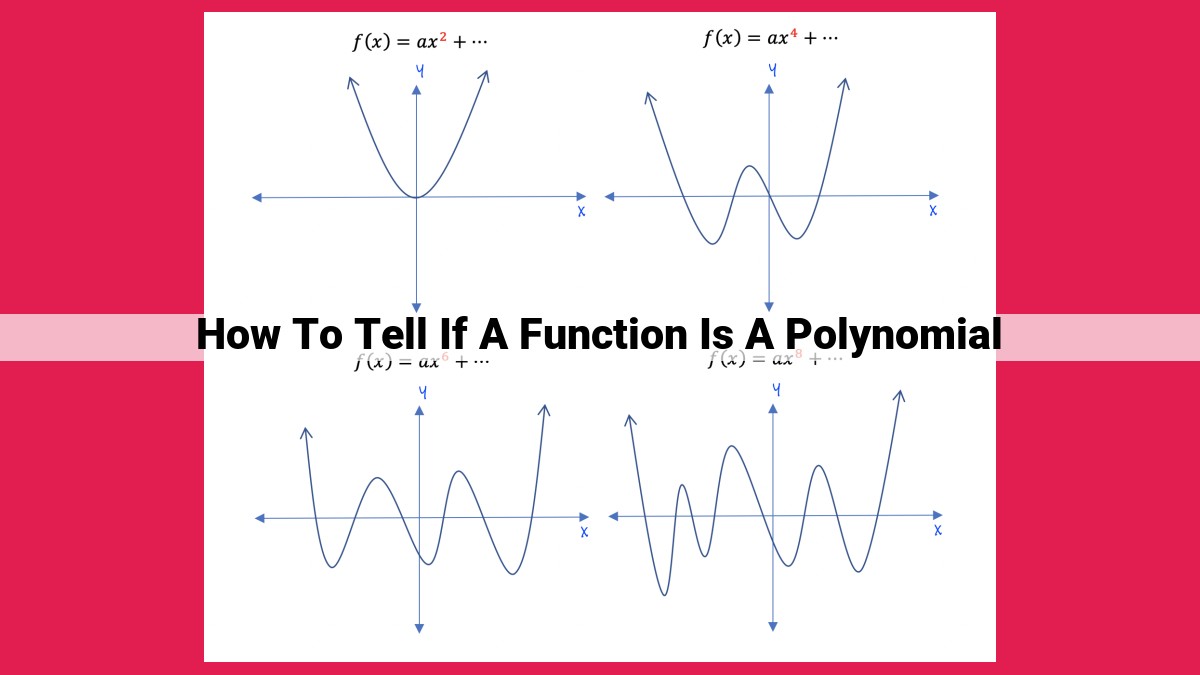
Every polynomial function has a degree, which represents the highest exponent of its variable. Just like buildings have stories, polynomials have degrees. The degree tells us how complex the function is, with each level representing a higher order of operation. For instance, a linear function has a degree of 1, while a quadratic function has a degree of 2.

Coefficients: The Numbers that Shape the Curve

Polynomial functions are made up of terms, each multiplied by a coefficient. These coefficients are the numbers that orchestrate the shape of the function’s graph. They determine how steep the curve is, where it turns, and where it intercepts the axes.

Constant Term: The Foundation of the Function

Every polynomial function has a constant term, a number that stands alone without any variable attached. It acts as the foundation for the function, setting the level at which it begins its ascent or descent. This term determines the y-intercept, the point where the graph crosses the y-axis.

Understanding these properties is essential for navigating the world of polynomial functions. They provide a framework for understanding how these equations work, allowing us to decode their behavior and harness their power for solving problems and modeling real-world phenomena.

Identifying Polynomial Functions

• Describe how to identify polynomial functions based on their degree.
• Provide examples of linear functions (degree 1), quadratic functions (degree 2), and cubic functions (degree 3).

Identifying Polynomial Functions

When it comes to categorizing functions, understanding polynomial functions is crucial. Polynomial functions are mathematical expressions that can be written as the sum of terms, each term having a non-negative integer exponent. These functions exhibit unique properties that set them apart from other function types.

Identifying Polynomial Functions by Degree

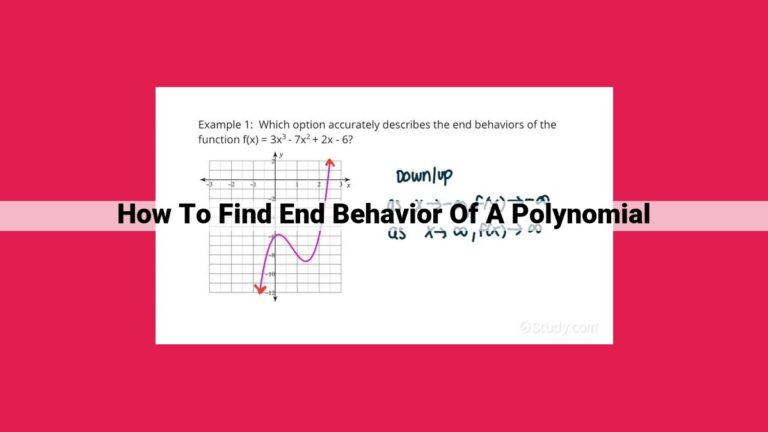
The degree of a polynomial function is the highest exponent of the variable in the function. Linear functions are polynomial functions with a degree of 1. They have the form f(x) = mx + b, where m is the slope and b is the y-intercept. For instance, f(x) = 2x + 1 is a linear function with a slope of 2 and a y-intercept of 1.

Quadratic functions are polynomial functions with a degree of 2. They have the form f(x) = ax² + bx + c, where a, b, and c are constants. For example, f(x) = x² - 4x + 3 is a quadratic function with a leading coefficient of 1, a linear coefficient of -4, and a constant term of 3.

Cubic functions are polynomial functions with a degree of 3. They have the form f(x) = ax³ + bx² + cx + d, where a, b, c, and d are constants. For instance, f(x) = x³ + 2x² - x + 1 is a cubic function with a leading coefficient of 1, a secondary coefficient of 2, a linear coefficient of -1, and a constant term of 1.

By understanding the degrees and forms of polynomial functions, you can easily identify them when you encounter them. These functions play a significant role in various fields, including mathematics, physics, and engineering.

Understanding the Distinctive Features of Polynomial Functions

In the realm of mathematics, polynomial functions reign supreme as expressions that can be depicted as a symphony of terms, each swaying to the rhythm of a non-negative integer exponent. Unlike their non-polynomial counterparts, these functions possess a unique set of characteristics that set them apart in the mathematical landscape.

1. Embracing All Real Numbers: The Universal Domain

Polynomial functions extend their welcoming invitation to all real numbers, embracing them as their boundless domain. This means that for any real number you may throw their way, they will respond with an output, never shying away from the challenge of computation.

2. Unveiling the Range: A Tale of Degree

The range of a polynomial function, the realm of its possible outputs, is a tale intertwined with its degree. For linear functions, the humble degree of one grants them a range as vast as the real numbers themselves. As the degree ascends, the range transforms, dictated by the leading coefficient’s whims and the constant term’s influence.

3. Intercepts: Where Curves Meet Axes

Polynomial functions often grace the x- and y-axes with their presence, marking the points where their curves gracefully intersect. The x-intercept whispers the secret of the function’s zeroes, unveiling where it grazes the x-axis. The y-intercept, a beacon of the constant term’s power, reveals the function’s value at the origin, where the journey of x begins.

Non-Polynomial Functions: Beyond the Realm of Polynomials

Polynomials, with their straightforward algebraic properties, often hold a special place in our mathematical toolkit. However, when functions venture beyond the realm of polynomials, a whole new world of mathematical possibilities unfolds. Meet non-polynomial functions, functions that challenge the familiar properties we’ve come to know and love.

Unlike polynomials, which are composed solely of terms with non-negative integer exponents, non-polynomial functions break free from these constraints. They can exhibit a diverse range of behaviors, making them indispensable tools for modeling complex phenomena.

Consider the graceful curves of rational functions, where polynomials take center stage in the numerator and denominator. Their intricate patterns arise from the interplay between polynomial and fractional expressions. Exponential functions, on the other hand, soar to infinity with breathtaking speed, as their outputs grow exponentially with the input. They capture the essence of processes where growth or decay occurs at a constant rate.

The rhythmic oscillations of trigonometric functions add a touch of elegance to the non-polynomial landscape. Their sinusoidal and cosinusoidal waves find applications in everything from sound waves to planetary motion.

Key Features of Non-Polynomial Functions

• They defy the non-negative integer exponent rule.
• They may exhibit complex algebraic expressions, including radicals, logarithms, and trigonometric functions.
• Their behavior can be nonlinear and unpredictable.

Applications of Non-Polynomial Functions

Non-polynomial functions play a pivotal role in numerous fields:

• Modeling population growth and decay
• Analyzing financial investments
• Simulating physical phenomena
• Solving differential equations

By embracing the power of non-polynomial functions, we expand our mathematical horizons and gain a deeper understanding of the intricate world around us.