How To Calculate Rectangle Height: Formulas, Techniques, And Applications

To find the height (or width) of a rectangle, use the area formula: Area = Length x Height. If you know the area and length, simply divide the area by the length to get the height. Another approach is to use the Pythagorean theorem for right-angled rectangles. If you know the diagonal length and one side length, you can use the formula: Height² = Diagonal² – Length². For similar rectangles, you can apply the ratio of length-to-width to find missing measurements. Additionally, trigonometry and indirect measurement techniques can be employed to determine inaccessible dimensions, using ratios and proportions to establish relationships between similar rectangles.

Understanding the Basics of Rectangles

• Describe the concept of a rectangle and its key features (length, width, perimeter, area).

Understanding Rectangles: A Journey into Geometric Simplicity

In the realm of geometry, rectangles stand out as pillars of simplicity and elegance. Their straight sides and right angles form a shape that is both recognizable and versatile.

At its core, a rectangle is defined by its length and width. Length refers to the horizontal measurement, while width indicates the vertical distance. These dimensions play a crucial role in determining a rectangle’s area and perimeter.

Area represents the space enclosed by a rectangle, calculated by multiplying its length by its width. Perimeter, on the other hand, denotes the distance around its edges, obtained by adding twice the length and twice the width. These measurements provide essential insights into a rectangle’s size and shape.

Understanding the relationship between these concepts is fundamental to unlocking the mysteries of rectangles. By manipulating the formulas for area and perimeter, we can solve for length or width when one is known. This enables us to analyze and compare rectangles with ease.

The Building Blocks of Rectangles: Area and Perimeter

In the realm of geometry, rectangles reign supreme as foundational shapes with a myriad of applications. Understanding their properties, particularly area and perimeter, is crucial for unlocking their mathematical secrets.

Area: A Measure of Space Within

Imagine a rectangle as a spacious dance floor, where the length and width serve as its dimensions. The area of a rectangle denotes the amount of space it encompasses, akin to the number of dancers that can gracefully twirl within its confines. The formula for calculating area is as simple as multiplying its length by its width:

Area = Length × Width

For instance, a rectangle with a length of 5 units and a width of 3 units would have an area of 15 square units – ample space for a small gathering.

Perimeter: Enclosing the Boundaries

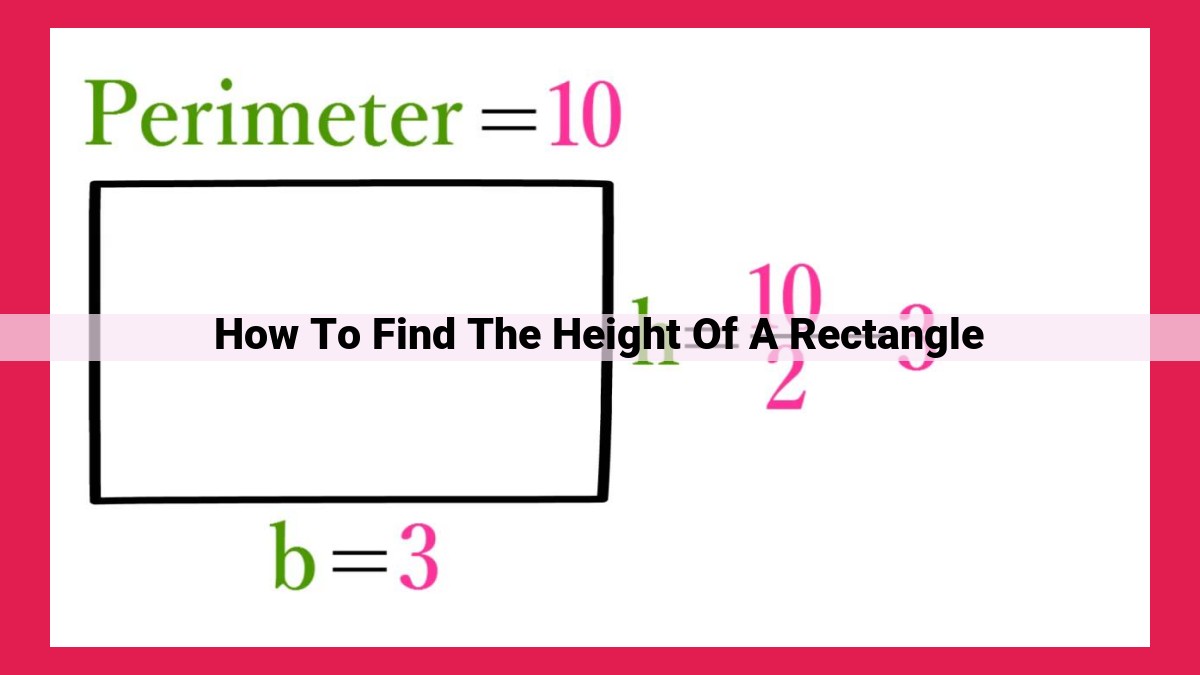
Now, envision the rectangle as a fenced-in enclosure, where the perimeter represents the total length of its fence. Unlike area, perimeter measures the distance around the rectangle’s edges, like a protective barrier. The formula for perimeter is equally straightforward:

Perimeter = 2 × (Length + Width)

Returning to our previous example, the perimeter of our 5-by-3 rectangle would be 2 × (5 + 3) = 16 units – a perfect size for a leisurely stroll along its periphery.

Area and Perimeter: A Dynamic Duo

The area and perimeter of a rectangle are not mere isolated calculations; they possess a symbiotic relationship. By knowing one, you can often determine the other, making them a versatile problem-solving tandem.

These formulas provide the cornerstone for exploring the captivating world of rectangles, unlocking their secrets and empowering us to unravel the mysteries of the geometric realm. Embrace the simplicity and power of these concepts, and witness how they transform your understanding of geometry forevermore.

Unraveling the Enigmatic Relationship between Length and Width in Rectangles

Rectangles, with their straightforward shape and key features, have piqued the curiosity of mathematicians and engineers alike. Their length and width play a pivotal role in determining their area and perimeter. Understanding the intricate dance between these dimensions empowers us to solve a myriad of problems.

Unveiling the Secrets of Area and Perimeter

The area of a rectangle, the space it encompasses, is calculated by multiplying its length and width (A = L × W). Similarly, its perimeter, the distance around its boundary, is found by summing the lengths of its four sides (P = 2 × (L + W)). These formulas serve as the foundation for delving into the relationship between length and width.

Resolving the Length or Width Quandary

Often, we encounter situations where only one of these dimensions is known. But fear not, for the area and perimeter formulas hold the key to resolving this dilemma. By equating the formula to a known value, we can solve for the unknown dimension. For instance, if the area is 50 square units and the length is 10 units, we can determine the width by setting A = L × W to 50 = 10 × W, yielding W = 5 units.

Illustrative Example

Suppose you have a rectangular plot of land with a perimeter of 120 meters. However, you only know that its length is twice its width. Using the perimeter formula, we can establish the equation:

P = 2 × (L + W)
120 = 2 × (2W + W)
120 = 2 × 3W
60 = 3W
W = 20 meters

Since the length is twice the width, L = 2 × 20 = 40 meters. Thus, the dimensions of the rectangular plot are 40 meters by 20 meters.

The Pythagorean Theorem: Unlocking the Secrets of Right-angled Rectangles

In the realm of geometry, rectangles stand tall as fundamental shapes, often encountered in our daily lives. From picture frames to construction blueprints, rectangles abound. Among these rectangular wonders lie a special breed known as right-angled rectangles, where two sides form a perfect right angle.

Within the tapestry of right-angled rectangles, a brilliant theorem unveils its power – the Pythagorean theorem. This legendary theorem, formulated by the enigmatic Greek mathematician Pythagoras, has stood the test of time, offering an invaluable tool for solving a myriad of geometric conundrums.

A Tale of Squares and Diagonals

Imagine a right-angled rectangle, its side lengths labeled as length and width. According to the Pythagorean theorem, the square of its diagonal (the hypotenuse of the right triangle formed by the length and width) is equal to the sum of the squares of the length and width. In equation form, it reads:

**Diagonal² = Length² + Width²**

Unraveling the Mystery of the Diagonal

The Pythagorean theorem empowers us to unravel the mystery of the diagonal’s length. Suppose we have a rectangle with a length of 6 units and a width of 8 units. To find the length of its diagonal, we simply plug these values into the formula:

**Diagonal² = Length² + Width²**
Diagonal² = 6² + 8²
Diagonal² = 36 + 64
Diagonal² = 100
Diagonal = √100
**Diagonal = 10 units**

Through this simple calculation, we have determined that the diagonal of our right-angled rectangle is 10 units long. Armed with the Pythagorean theorem, we can uncover the hidden secrets of any right-angled rectangle.

Similar Triangles and Rectangles: Unveiling Hidden Relationships

In the realm of geometry, rectangles hold a special place. They possess a distinct shape, characterized by four right angles and parallel sides. While their simplicity may seem unassuming, rectangles conceal a fascinating connection to triangles.

Delving into the concept of similar triangles, we encounter a powerful tool that allows us to establish relationships between different rectangles. Similar triangles share the same shape, but they may differ in size. This geometric kinship reveals a remarkable pattern when it comes to rectangles.

Consider two rectangles, aptly named Rectangle A and Rectangle B. If we draw diagonals in both rectangles, we create four right triangles. Surprisingly, the ratios of the perimeters, lengths, and widths of these two rectangles are equal. This observation paves the way for a fundamental property:

Ratio of Perimeters, Lengths, and Widths in Similar Rectangles

Let’s denote the perimeters, lengths, and widths of Rectangle A as P₁, L₁, and W₁, respectively. Similarly, for Rectangle B, we have P₂, L₂, and W₂. The ratio of perimeters is P₁:P₂. The ratio of lengths is L₁:L₂, and the ratio of widths is W₁:W₂.

Remarkably, these ratios are all equal:

P₁:P₂ = L₁:L₂ = W₁:W₂

This property unlocks a treasure trove of problem-solving opportunities. By knowing the dimensions of one rectangle and the ratio of perimeters, lengths, or widths, we can effortlessly determine the unknown dimensions of the other.

The concept of similar triangles and rectangles is a testament to the elegance and interconnectedness of geometry. It’s a tool that empowers us to explore the hidden relationships that shape the world around us.

Indirect Measurement Using Trigonometry

When it comes to measuring the world around us, we often encounter situations where direct measurement is challenging or impossible. That’s where indirect measurement comes into play, a technique that allows us to determine the dimensions of objects without physically accessing them.

Trigonometry, the study of angles and triangles, provides a powerful tool for indirect measurement. By utilizing trigonometric ratios, such as sine, cosine, and tangent, we can calculate the lengths of sides and angles in inaccessible triangles, thereby solving for unknown measurements in rectangles.

For instance, let’s say you want to determine the height of a tree without climbing it or using a measuring tape. You notice a nearby building of known height and measure the angles between the ground, the top of the tree, and the top of the building. Using trigonometry, you can calculate the tree’s height without ever directly touching it.

The key principle behind this technique is the law of similar triangles: if two triangles have the same shape but different sizes, the ratios of their corresponding sides are equal. By constructing similar triangles with one side known (e.g., the distance to the tree), you can use trigonometric ratios to find the unknown sides (e.g., the tree’s height).

Trigonometric indirect measurement also finds applications in surveying, architecture, and navigation. By employing principles of geometry and trigonometry, engineers and surveyors can determine the distance between inaccessible points, design structures with accuracy, and chart courses for ships and airplanes.

The beauty of indirect measurement using trigonometry lies in its versatility and precision. It allows us to measure distances, heights, and angles in challenging situations, empowering us to better understand and navigate our surroundings.

Ratios and Proportions: Unlocking Missing Measurements in Rectangles

In the realm of geometry, rectangles often hold a special place as symbols of precision and symmetry. Understanding their properties and relationships not only enhances our mathematical knowledge but also provides valuable tools in various practical applications. Among these properties, ratios and proportions play a crucial role in unlocking the secrets of these versatile shapes.

When dealing with similar rectangles, we discover an intriguing connection between their dimensions and measurements. Rectangles are considered similar if they share the same shape, meaning that their corresponding sides are proportional. This proportionality can be expressed using ratios, which compare the values of these measurements.

Unraveling Proportions

For instance, let’s consider two similar rectangles with lengths of 6 cm and 8 cm, respectively. The ratio of their lengths can be written as 6:8. This ratio suggests that the length of one rectangle is two-thirds (6/8) of the length of the other. Similarly, the ratio of their widths might be 4:6, indicating that the width of the smaller rectangle is equivalent to two-thirds (4/6) of the width of the larger rectangle.

Ratios as Measurement Magicians

The power of ratios extends beyond mere comparisons. They can also be used to determine missing measurements in similar rectangles. This becomes especially useful when we have access to only partial information about the shape.

Suppose we know that one similar rectangle has a length of 10 cm and a width-to-length ratio of 2:3. To find the missing width, we can set up a proportion:

Width / Length = 2/3
Width / 10 cm = 2/3
Width = (2/3) * 10 cm
Width = 6.67 cm

Ta-da! We have successfully determined the unknown width using the ratio and the known length.

Proportions in Real-World Applications

The principles of ratios and proportions find practical applications in various fields. Architects and engineers use them to scale designs and ensure structural integrity. Artists rely on them to maintain proportions in their drawings and paintings. Even in everyday life, proportions can help us with tasks such as determining the correct dosage of medication or mixing ingredients in a recipe.

In conclusion, ratios and proportions are indispensable tools in geometry, allowing us to explore the hidden relationships between measurements and dimensions in similar rectangles. They provide a powerful means to unlock missing information and solve problems, making them invaluable in both theoretical and practical endeavors.

Unlocking the Treasure Trove of Rectangle Geometry

Embark on a геометрический adventure as we unveil the secrets of rectangles, the quintessential building blocks of our world. From their unassuming beginnings to their remarkable properties, we’ll explore the fascinating world of these geometric marvels.

Rectangles, defined by their parallel sides and right angles, are more than just shapes; they’re a canvas for geometric exploration. Their area, the measure of the space they enclose, can be calculated with ease using the formula Length x Width. The perimeter, the distance around their boundary, is equally straightforward to determine: 2 x (Length + Width).

Now, let’s delve into their length and width relationships. Suppose you know the area and perimeter of a rectangle. Using some geometric wizardry, you can solve for either length or width, proving that information begets information in this mathematical wonderland.

But rectangles hold another secret: the Pythagorean theorem. When a rectangle flaunts a right angle, this theorem steps into the spotlight. It reveals the mesmerizing relationship between the sides and the diagonal, connecting them in a beautiful geometric dance.

Venturing further into the realm of geometry, we encounter similar triangles and rectangles. Like mirror images, similar figures share the same shape but differ in size. Understanding this concept unlocks the secrets to unlocking ratios of perimeter, length, and width for rectangles, revealing a world of hidden connections.

And let’s not forget the magic of indirect measurement. Trigonometry, the study of triangles, empowers us to measure inaccessible distances by using angles. It’s like a geometric detective, solving mysteries with precision and grace.

Finally, we culminate our journey by summarizing the key geometry concepts that shape rectangles: area, perimeter, volume, and shape. These concepts, like threads in a tapestry, weave together to create the fabric of rectangle geometry.