How To Calculate P-Values From Z-Scores For Statistical Inference
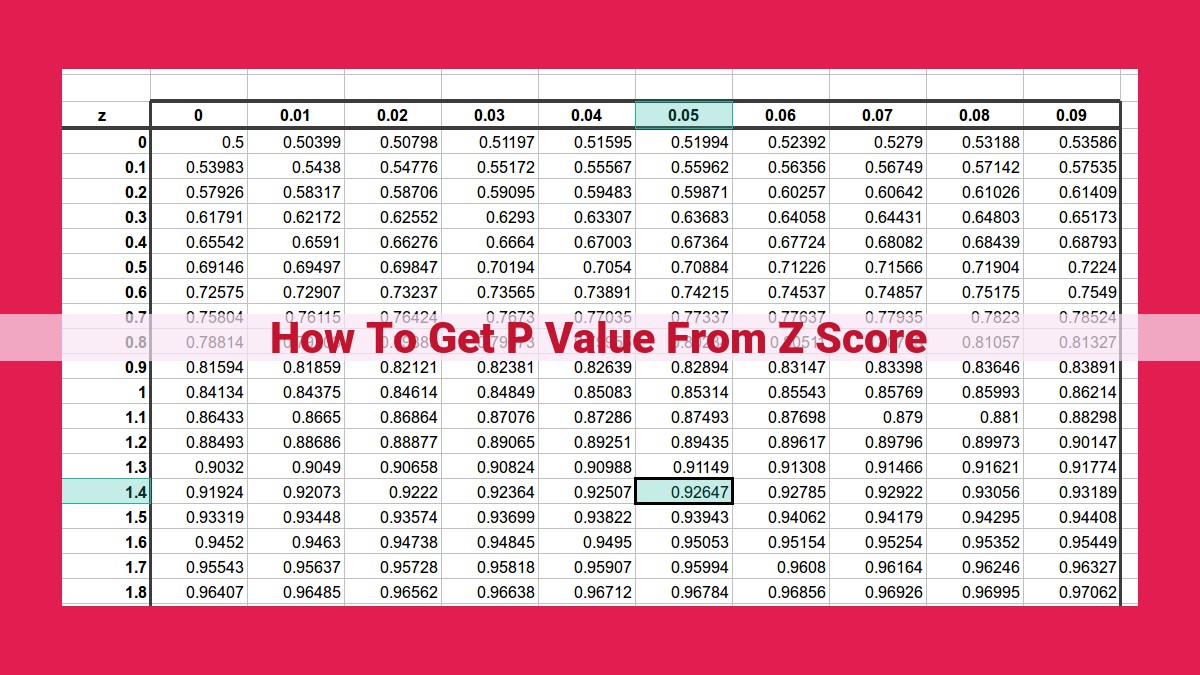
To derive a P-value from a Z-score, begin by understanding the Z-distribution and calculating the Z-score using the formula (X – μ) / σ. Next, determine if it’s a one-tailed or two-tailed test and identify the relevant critical value(s). For a one-tailed test, calculate the P-value as the area under the Z-curve beyond the critical value. For a two-tailed test, calculate the P-value as the sum of the areas under the Z-curve beyond each critical value.
Understanding the Significance of P-Values and Z-Scores in Statistical Analysis
In the realm of data analysis, P-values and Z-scores emerge as indispensable tools, offering valuable insights into the statistical significance of our findings. They guide us in making informed decisions, ensuring that our conclusions are not merely based on chance but are rooted in statistical evidence.
Z-scores are a measure of how many standard deviations a particular data point lies away from the mean. This allows us to compare observations within a dataset and assess their relative distance from the central tendency. P-values, on the other hand, represent the probability of observing a result as extreme or more extreme than the one obtained, assuming the null hypothesis is true.
The relationship between these two concepts is profound. Z-scores provide a measure of the deviation from the expected value, while P-values quantify the statistical significance of that deviation. By understanding this interplay, we gain a deeper comprehension of the strength and reliability of our findings.
Understanding the Standard Normal Distribution (Z-Distribution)
Imagine yourself at a crowded school carnival, surrounded by an endless sea of games and activities. Amidst the chaos, your gaze falls upon a peculiar booth adorned with a large bell curve. This is the world of the standard normal distribution, also known as the Z-distribution.
Just like the bell curve you encounter at the carnival, the standard normal distribution is a symmetrical bell-shaped curve that describes the probability of random variables in a large population. It has a mean of 0 and a standard deviation of 1, making it the basis for standardizing data and comparing it across different distributions.
The Z-score is a pivotal concept in the standard normal distribution. It measures how far a particular data point deviates from the mean in units of standard deviation. A Z-score of 0 indicates that the data point is exactly at the mean, while a positive Z-score implies that it lies to the right of the mean and a negative Z-score signifies it lies to the left.
Z-scores play a crucial role in determining the statistical significance of data. They allow us to quantify the probability of a particular value occurring in the distribution. This probability is known as the P-value. For instance, a Z-score of 2 corresponds to a P-value of 0.023, which means that there is only a 2.3% chance of observing a value that extreme or more extreme in the standard normal distribution.
Calculating Z-Scores: Measuring Deviation and Statistical Significance
In the realm of statistics, Z-scores and P-values play pivotal roles in unraveling the significance of data. To fully appreciate the significance of these statistical measures, delving into the intricacies of Z-scores is essential.
The Z-score, denoted by the symbol Z, is a standardized measure that quantifies the deviation of a data point (X) from the mean (μ) in terms of standard deviations (σ). The formula for calculating Z-scores is:
Z = (X - μ) / σ
A positive Z-score indicates that the data point lies above the mean, while a negative Z-score suggests it falls below the mean.
Interpreting Z-Scores
The magnitude of a Z-score conveys important information about the relative position of the data point within a distribution. For instance, a Z-score of 2.5 implies that the data point lies 2.5 standard deviations above the mean, whereas a Z-score of -1.2 signifies that it is 1.2 standard deviations below the mean.
One-Tailed Test vs. Two-Tailed Test
Z-scores can be employed in both one-tailed and two-tailed tests. A one-tailed test is used when one has a specific direction in mind (e.g., testing if the mean is higher or lower than a certain value). A two-tailed test, on the other hand, is used when no specific direction is specified.
In a one-tailed test, the rejection region (the area where the null hypothesis is rejected) lies in one tail of the distribution, while in a two-tailed test, it spans both tails. The choice of test type depends on the research question and the hypotheses being tested.
**The Significance of P-Values: Unlocking Statistical Clues**
In the realm of statistics, P-values play a pivotal role in unlocking the secrets of data, guiding our understanding of research findings. They are like forensic detectives, sifting through statistical evidence to help us make informed decisions and draw meaningful conclusions.
At their core, P-values measure the probability of obtaining a test statistic as extreme or more extreme than the one we observed, assuming our null hypothesis is true. They are expressed as numbers between 0 and 1, with smaller values indicating a lower probability of obtaining such an extreme result.
The Relationship between P-values and Z-scores
P-values and Z-scores are intimately connected. Z-scores measure how many standard deviations a data point lies from the mean of its distribution. They provide a standardized way to compare values from different distributions. Crucially, P-values can be calculated from Z-scores using the formula:
P(Z) = 1 - P(-Z)
This relationship highlights that P-values and Z-scores are two sides of the same coin, providing complementary perspectives on the statistical significance of a result.
P-Values and Hypothesis Testing
Hypothesis testing is a fundamental statistical method used to evaluate whether a particular hypothesis is supported by the data. In hypothesis testing, the P-value plays a pivotal role in determining whether we can reject the null hypothesis and conclude that the alternate hypothesis is true.
Typically, we choose a significance level, which represents the threshold of P-value below which we reject the null hypothesis. If the P-value is lower than the significance level, it suggests that the data is unlikely to have occurred by chance and that the alternate hypothesis is likely true. Conversely, if the P-value is higher than the significance level, we fail to reject the null hypothesis, indicating that the data is consistent with the null hypothesis.
Applications of P-Values
P-values have broad applications across various fields, including:
- Medicine: Evaluating the effectiveness of new treatments
- Psychology: Measuring the impact of interventions on behavior
- Finance: Assessing the risk of investment decisions
- Social sciences: Testing theories about human behavior
Understanding P-values is essential for interpreting statistical results and making informed data-driven decisions. By comprehending their significance and their relationship with Z-scores, you can unlock the power of statistics and gain valuable insights from your data.
Using Z-Scores to Calculate P-Values
Understanding the relationship between Z-scores and P-values is crucial in statistical analysis. In this section, we’ll explore how to calculate P-values from Z-scores for both one-tailed and two-tailed tests.
One-Tailed Test
In a one-tailed test, we hypothesize that the population mean is either greater than or less than a specified value. To calculate the P-value:
- Determine the critical value: Based on the level of significance (α), find the critical value (Zc) from the standard normal distribution table.
- Identify the rejection region: The rejection region is the area under the Z-curve that lies beyond the critical value. If the Z-score falls in the rejection region, we reject the null hypothesis.
- Calculate the P-value: The P-value is the area under the Z-curve that lies beyond the critical value. This area represents the probability of obtaining a Z-score as extreme as or more extreme than the observed Z-score, assuming the null hypothesis is true.
Two-Tailed Test
In a two-tailed test, we hypothesize that the population mean is different from a specified value. To calculate the P-value:
- Establish two critical values: Based on the level of significance (α), find two critical values (Zc1 and Zc2) from the standard normal distribution table, such that α is divided equally between the two tails.
- Divide the rejection region: The rejection region is divided into two tails, each with an area of α/2. We reject the null hypothesis if the Z-score falls in either tail.
- Compute the P-value: The P-value is the sum of the areas under the Z-curve that lie beyond each critical value. This area represents the probability of obtaining a Z-score as extreme as or more extreme than the observed Z-score, assuming the null hypothesis is true.