Glide Reflection: Combining Reflection And Translation For Unique Patterns

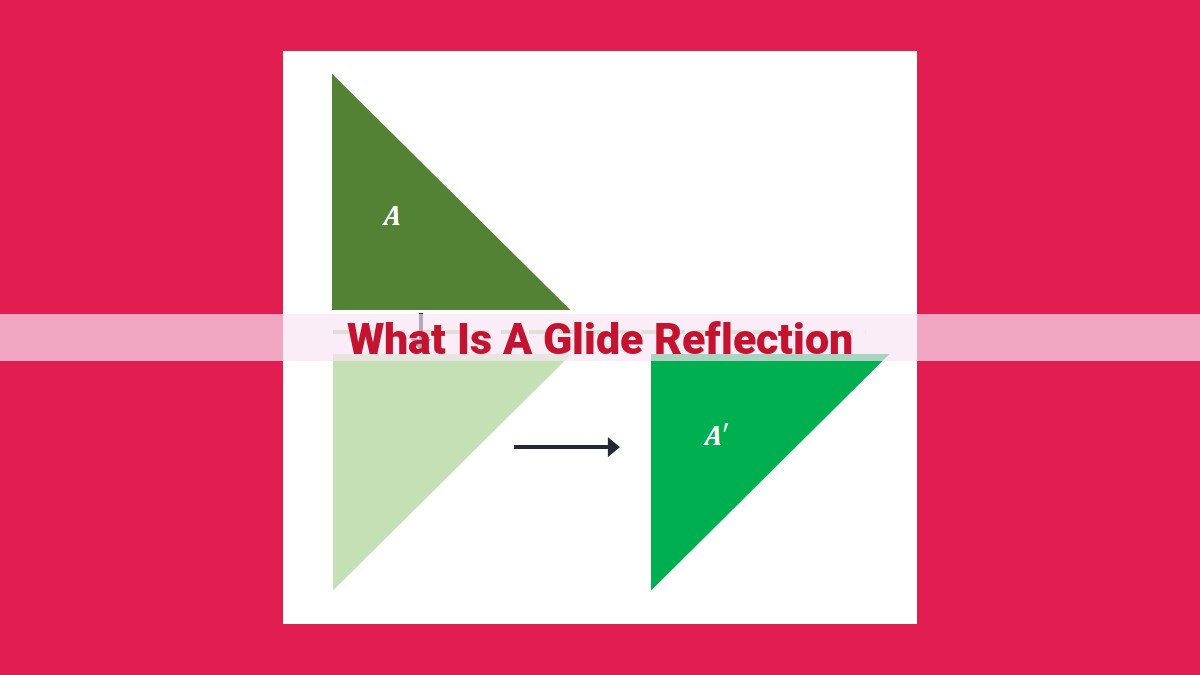
A glide reflection is an isometry that combines reflection and translation. It flips a figure across a line and then translates it parallel to the glide line, preserving congruence and similarity. Unlike reflections and translations alone, glide reflections have both perpendicular and parallel components, creating unique patterns and mirror images.

• Definition: A transformation combining reflection and translation.
• Type of isometry: Preserves congruence, similarity, equal area, and orientation.

Glide Reflections: A Journey through Symmetry and Transformation

In the realm of geometry, we encounter a fascinating transformation known as glide reflection. It’s a unique dance between two fundamental transformations: reflection and translation, creating a captivating blend of symmetry and movement.

Unveiling the Essence of Glide Reflections

A glide reflection is a geometric isometry, meaning it preserves the inherent properties of a shape. During this transformation, a figure undergoes a reflection across a line, followed by a translation along the line of reflection. This precise combination gives rise to a mirror image that appears shifted to one side.

Crucially, glide reflections adhere to the tenets of isometry. They maintain the congruence, similarity, equal area, and orientation of the original figure. This implies that distances and angles remain unchanged, ensuring a faithful representation of the original shape.

Exploring the Interplay of Reflection and Translation

At the heart of glide reflections lies the interplay of two distinct transformations. Reflection involves flipping a figure across a line, creating a mirror image. The line across which reflection occurs is known as the line of reflection. Meanwhile, translation denotes the movement of a figure without rotating or reflecting it. This movement is characterized by a vector that defines its direction and distance.

Unveiling the Glide Line and Glide Plane

Glide reflections involve two key elements: the glide line and glide plane. The glide line is the line along which the reflection and translation take place. The glide plane, on the other hand, is a plane that is perpendicular to the glide line and contains the reflection plane. The reflection plane is the line across which reflection occurs.

Glide reflections hold a prominent place in the world of geometry. They elegantly combine symmetry and movement, offering a deeper understanding of geometric transformations. Beyond their theoretical importance, glide reflections find practical applications in diverse fields such as art, design, and engineering. By understanding the nuances of glide reflections, we unlock the secrets of symmetry and its captivating role in shaping our world.

Isometry: Equal Measure

Isometry is a fascinating concept in geometry that describes transformations where equal measure is preserved. Glide reflections, among other transformations, are examples of isometries.

When we say “equal measure,” we mean that the distances and angles within a figure remain unchanged under the transformation. This means that glide reflections do not distort or stretch the figure, maintaining its congruence.

Another way to think about isometry is that it is the preservation of similarity, which means that the shape and proportions of the figure remain the same. This is in contrast to non-isometric transformations like stretching or shearing, which alter the figure’s shape.

Glide reflections also share a close relationship with congruence, which is the property of two figures being identical in shape and size. Since glide reflections maintain congruence, they inherently preserve equal area.

Isometry is a fundamental concept in geometry, providing a way to classify and understand transformations that maintain the integrity of figures. It is essential in fields like architecture, where maintaining the proportions of structures is crucial.

Reflection: Flipping Across a Line

• Definition: Reflection flips a figure across a line.
• Line of reflection and mirror image.
• Perpendicular bisector in relation to reflection.

Reflection: Flipping Across a Line

In the realm of geometry, where shapes dance and transformations unfold, we encounter the enigmatic concept of reflection. Reflection is the act of flipping a figure across a line, creating a mirror image that dances and swirls in a mirror-like symmetry.

The line of reflection serves as the dividing line between the original figure and its reflection. It’s like a boundary that separates the world as it is from its doppelganger. When a figure undergoes reflection, every point on one side of the line is mirrored to the corresponding point on the other side, creating a perfect, symmetrical twin.

The mirror image is a reflection’s faithful companion, identical in size, shape, and orientation to the original figure. It’s as if the figure has stepped through a magical portal, emerging on the other side with its every detail intact, save for the subtle inversion that whispers of a reflection’s presence.

One intriguing property of reflection is its reliance on the perpendicular bisector. The perpendicular bisector is a line that intersects the line of reflection at a right angle, creating two identical half-planes. The original figure and its reflection lie symmetrically on either side of the perpendicular bisector, confirming the reflection’s mirror-like precision.

Reflection plays a pivotal role in creating patterns, designs, and symmetries that adorn our world. From the mesmerizing patterns in Islamic art to the intricate tessellations of nature, reflections dance and intertwine, creating a breathtaking tapestry of visual wonder.

Translation: A Journey Without Twists or Turns

Embark on a geometric expedition, where we explore the intriguing world of translations. Unlike reflections that flip or rotations that spin, translations offer a straightforward journey. They carry figures from one point to another, preserving their shape, size, and orientation.

Vectors: Guiding the Path

Just like a compass guides a traveler, vectors direct the path of translation. These mathematical arrows point the direction and distance of the movement. The length of the vector indicates the magnitude of the translation, while its direction determines the route.

Parallel Paths: A Steady Course

Think of a train gliding along a straight track. That’s parallel translation in action! Figures move along a straight line, maintaining their original orientation. The distance and direction remain constant throughout the journey, making parallel translation a smooth and predictable transformation.

Applications: Beyond the Classroom

Glide reflections find their way into a fascinating array of applications, from art and design to engineering and even everyday life. They create mesmerizing patterns in architecture, enhance movement in animation, and enable efficient machinery operations.

Translations, along with reflections and rotations, form the cornerstone of isometries, a group of transformations that preserve congruent figures. They provide a foundation for understanding complex geometric concepts and have practical applications that touch various aspects of our world.

**Glide Lines: Unraveling the Secrets of Reflection and Translation**

In the realm of geometry, transformations play a pivotal role in shaping and manipulating figures. One such transformation, that of the glide reflection, stands out as a captivating combination of reflection and translation, unlocking a world of possibilities. As we delve into this fascinating concept, let’s embark on a journey to unravel the secrets of the glide line.

A glide line, a primordial entity in the world of transformations, weaves together the elegance of reflection and the dynamism of translation. Imagine reflecting a figure across a line, then sliding it along that same line. You’ve essentially performed a glide reflection!

The reflection plane, the boundary that governs the mirroring action, stands perpendicular to the glide line, creating a mirror image with respect to the reflection plane. As if by magic, the figure transforms, its reflection shimmering across the mirror image.

With a flick of the wrist, the figure then embarks on a translation journey along the glide line, gliding smoothly and effortlessly. This translation vector, a guiding force, propels the figure to its new destination, leaving behind a trail of congruent transformations.

The glide line, acting as a master choreographer, orchestrate the intricate interplay between reflection and translation, leading to an array of breathtaking geometric patterns. These patterns adorn the canvases of art, inspire intricate designs, and find applications across a wide range of fields, from architecture to materials science.

So, there you have it – the elusive glide line, a transformative force that combines the power of reflection and translation. As we continue our geometric explorations, may the glide line serve as a beacon of geometric ingenuity, guiding us through the fascinating world of transformations.

The Intriguing World of Glide Planes: Combining Reflection and Translation

In the enchanting realm of geometry, the concept of glide planes takes center stage as a fascinating amalgamation of reflection and translation. Let’s dive into this captivating dance of transformations and explore its captivating nature.

Imagine a glide plane as an imaginary flat surface that acts as a mirror image generator. When a figure interacts with this plane, it is reflected across it, creating an identical twin that exists on the opposite side. The translation component comes into play as the original figure then slides parallel to the glide plane, generating a congruent copy of itself.

This remarkable combination of reflection and translation unveils a mirror image that is both familiar and slightly shifted. Intriguingly, the translation distance is always perpendicular to the line of reflection. It’s as if the figure has taken a dance step, mirroring its former self before gracefully gliding to a new location.

The allure of glide planes extends beyond their conceptual beauty. These transformations hold immense significance in the realm of isometry. Isometries are special transformations that preserve vital geometric properties such as shape, size, and angles. Simply put, if you apply an isometry to a figure, it essentially looks the same as before, just in a different spot. Glide reflections, being isometries, maintain these cherished properties, showcasing their remarkable ability to manipulate figures while preserving their intrinsic qualities.