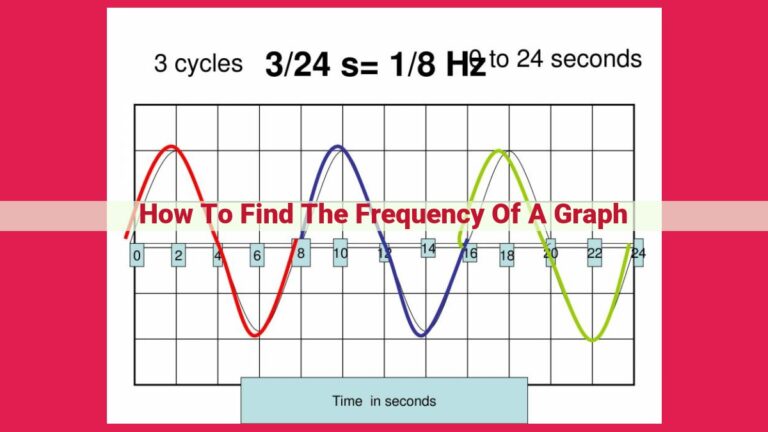
Understanding Frequency And Period: A Reciprocal Relationship In Science And Engineering

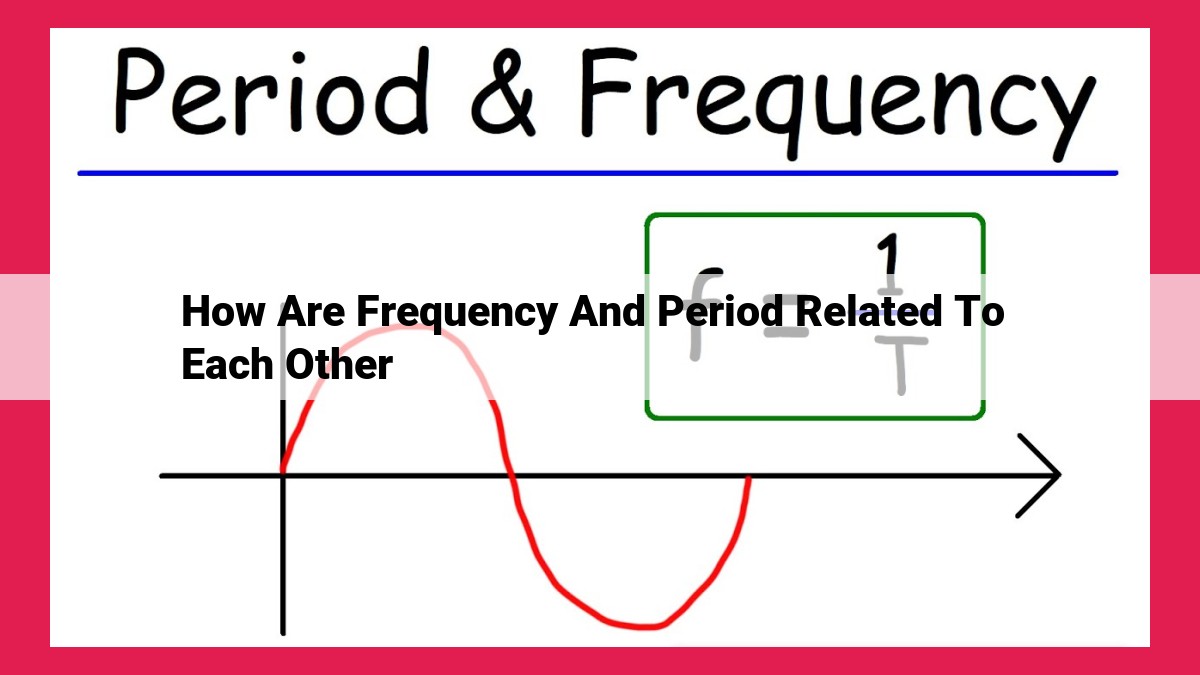
Frequency and period are inversely related, sharing a reciprocal relationship. Frequency measures the number of occurrences within a time unit, while period represents the time interval between those occurrences. The formula f = 1/T and T = 1/f demonstrates this inverse relationship, indicating that as frequency increases, period decreases, and vice versa. This concept finds applications in fields like medicine, signal processing, and mechanics, where understanding the frequency and period of signals and oscillations is crucial for analysis and design.

Understanding Frequency and Period: A Journey into the Rhythms of Nature

In the realm of science and engineering, two fundamental concepts that govern the rhythmic motion of waves and oscillations are frequency and period. They play a crucial role in understanding phenomena from the beating of our hearts to the transmission of data.

Frequency, denoted by the symbol f, measures the number of cycles or repetitions that occur in a given unit of time. It is expressed in units of hertz (Hz), with one hertz representing one cycle per second. Period, on the other hand, symbolized by T, represents the duration of a single cycle. Measured in seconds (s), it tells us how long it takes for a full oscillation to complete.

The interplay between frequency and period is an intriguing dance. They are inversely proportional to each other, meaning as frequency increases, period decreases, and vice versa. This relationship is captured by the mathematical formula:

f = 1 / T

This formula serves as a bridge between the two concepts, allowing us to easily convert between frequency and period. For instance, if a wave has a frequency of 10 Hz, its period would be 0.1 seconds.

Understanding frequency and period is essential for comprehending a wide range of phenomena in our world. In medical diagnostics, electrocardiograms (ECGs) rely on the frequency of heartbeats to assess heart health. In signal processing, frequency plays a crucial role in transmitting data over communication channels. Moreover, in mechanical vibrations, frequency and period are key to understanding the behavior of engines and musical instruments.

As we conclude our journey into the world of frequency and period, we recognize their interconnectedness and significance. They are the heartbeat of our universe, governing the rhythmic motion of waves and oscillations. Understanding their relationship is key to unlocking the secrets of nature and unlocking the power of technology.

Frequency: The Rhythm of the Universe

In the symphony of life, everything oscillates at its own unique rhythm, described by two fundamental concepts: frequency and period. They are the heartbeat of the universe, shaping the world we experience.

Frequency, measured in Hertz (Hz), is the number of cycles or repetitions of a periodic event per unit time. It represents the rate at which something happens. Think of a beating heart or a vibrating guitar string. The higher the frequency, the faster the repetition or vibration.

Period, on the other hand, is measured in seconds (s). It is the duration of one complete cycle or oscillation. It is the inverse of frequency. The longer the period, the slower the repetition or vibration. For instance, a heart rate of 60 beats per minute (bpm) would have a period of 1 second (60 s / 60 bpm = 1 s).

Interestingly, frequency and period have an inverse relationship. As the frequency increases, the period decreases, and vice versa. This relationship is mathematically expressed by the formula:

f = 1/T

Where:

• f is the frequency (in Hz)
• T is the period (in s)

This inverse relationship is crucial for understanding various phenomena, such as wave motion. For example, high-frequency waves have shorter wavelengths and travel faster than low-frequency waves.

Period: The Duration of a Cycle

In the symphony of motion, there exists a rhythmic dance of waves, oscillations, and vibrations. To fully comprehend these dynamic phenomena, we must delve into two fundamental concepts: frequency and period.

Period represents the duration of a single complete cycle in this rhythmic motion. Imagine a pendulum swinging back and forth. The period is the time it takes for the pendulum to complete one full swing, from its starting point to its highest point and back to its starting point. It is measured in seconds (s).

Period and Frequency: An Inverse Relationship

Period is a fascinating concept, intricately connected to its counterpart, frequency. Frequency measures how often a cycle occurs in a given unit of time, typically per second. These two quantities engage in an inverse dance. As frequency increases, the period decreases, and vice versa.

This inverse relationship can be expressed mathematically:

**Period (T) = 1/Frequency (f)**

This formula elegantly illustrates their interdependence. For instance, if a cycle repeats twice every second, its frequency is 2 Hz (hertz), and its period is 0.5 seconds.

Understanding the concept of period empowers us to analyze and interpret a wide range of phenomena. From the rhythmic beating of our hearts to the vibrations of guitar strings, period provides a crucial lens through which we can unlock the secrets of the dynamic world around us.

The Interplay of Frequency and Period: An Inverse Romance

Frequency and period, two inseparable concepts in the realm of oscillations, share a captivating dance that mirrors the delicate balance of their existence. Like a seesaw, as one ascends, the other gracefully descends.

The inverse relationship between frequency and period is mathematically encapsulated in the formula:

f = 1/T

Here, f represents the frequency, measured in Hertz (Hz), and T signifies the period, expressed in seconds (s). This equation reveals the fundamental connection between the two: as frequency increases, period decreases, and vice versa.

Imagine a pendulum swinging back and forth. The frequency of its oscillations, measured in Hz, describes how many times it completes a full swing in one second. Simultaneously, the period, measured in seconds, represents the time it takes for the pendulum to complete one full swing. The faster the pendulum swings (higher frequency), the shorter the time it takes for each swing (shorter period).

This inverse relationship finds myriad applications in diverse fields. In medical diagnostics, electrocardiograms (ECGs) rely on the frequency and period of electrical signals to assess heart health. In signal processing, manipulating frequency and period is crucial for efficient data transmission. Furthermore, engineers analyze the frequency and period of mechanical vibrations in engines and musical instruments to enhance performance and prevent damage.

Understanding the inverse relationship between frequency and period provides a deeper comprehension of wave motion and other phenomena. For instance, in a sound wave, the frequency determines the pitch we hear, while the period influences the duration of each sound. By adjusting these parameters, musicians create melodies and harmonies that resonate with our emotions.

In essence, frequency and period are two sides of the same coin, inextricably linked through their inverse relationship. Whether analyzing heartbeats, transmitting data, or creating symphonies, this interplay lies at the heart of understanding the rhythmic tapestry that surrounds us.

Converting Between Frequency and Period: A Simple Formula for Understanding Wave Patterns

In the realm of physics and beyond, understanding the concepts of frequency and period is essential for unraveling the mysteries of waves and their behavior. Frequency measures the number of oscillations (peaks or troughs) that occur within a specific time frame, while period represents the duration between consecutive peaks.

The relationship between frequency (f) and period (T) is an inverse one, meaning they are inversely proportional. This means that as the frequency increases, the period decreases, and vice versa. This inverse relationship can be beautifully captured by the simple yet powerful formula:

f = 1/T

T = 1/f

This formula acts as a bridge between frequency and period, allowing us to effortlessly convert between the two measurements. For instance, if a wave has a frequency of 5 oscillations per second, its period would be 1/5 second, or 0.2 seconds.

The ability to convert between frequency and period is a valuable tool in various fields. In medical diagnostics, electrocardiograms (ECGs) use frequency to measure heart rate and detect abnormalities. Signal processing in telecommunications relies on frequency to transmit data efficiently. Mechanical vibrations in engines and musical instruments are also analyzed using frequency and period measurements.

By understanding the interconnectedness of frequency and period, we gain deeper insights into the rhythmic patterns and periodic phenomena that surround us. From the heartbeat to the hum of an engine, the formula f = 1/T illuminates the symphony of waves and their fundamental characteristics.

Real-World Applications of Frequency and Period

In the realm of science, technology, and countless other fields, frequency and period play pivotal roles. These two interconnected concepts find their applications in a diverse range of real-world scenarios, from the depths of medical diagnostics to the intricate world of signal processing and the rhythmic vibrations of the physical world.

In the field of medical diagnostics, frequency and period are of paramount importance. Electrocardiograms (ECGs), a cornerstone of cardiac health monitoring, rely on analyzing the electrical impulses of the heart. The frequency of these impulses, measured in beats per minute, provides crucial information about the heart’s rhythm and overall functionality. Similarly, in brainwave monitoring, the period of brainwaves, measured in milliseconds, offers insights into brain activity and can aid in diagnosing neurological disorders.

Signal processing, a key component of modern communication systems, heavily relies on frequency and period. The frequency of a signal determines the amount of data that can be transmitted per unit of time. The higher the frequency, the greater the data transmission rate. Similarly, in data storage devices like hard drives, the period of magnetic pulses plays a vital role in determining the speed and efficiency of data storage and retrieval.

The realm of mechanical vibrations is another arena where frequency and period hold immense significance. In engines, the frequency of vibrations can indicate potential mechanical faults, allowing for timely maintenance and prevention of catastrophic failures. Conversely, in musical instruments, the period of vibrations determines the pitch of the sound produced. From the resonant frequencies of guitar strings to the intricate overtones of wind instruments, frequency and period are the essential ingredients that orchestrate the symphony of music.

The interconnectedness of frequency and period extends far beyond these examples, with their applications pervasive in many other scientific and technological domains. Understanding the interplay between these two concepts not only enriches our knowledge of the physical world but also empowers us to harness their power in myriad ways. From medical advancements to technological breakthroughs and the exploration of the sonic landscape, the world as we know it is shaped in countless ways by the symphony of frequency and period.