Finding Slope Of Parallel Lines: A Comprehensive Guide For Seo

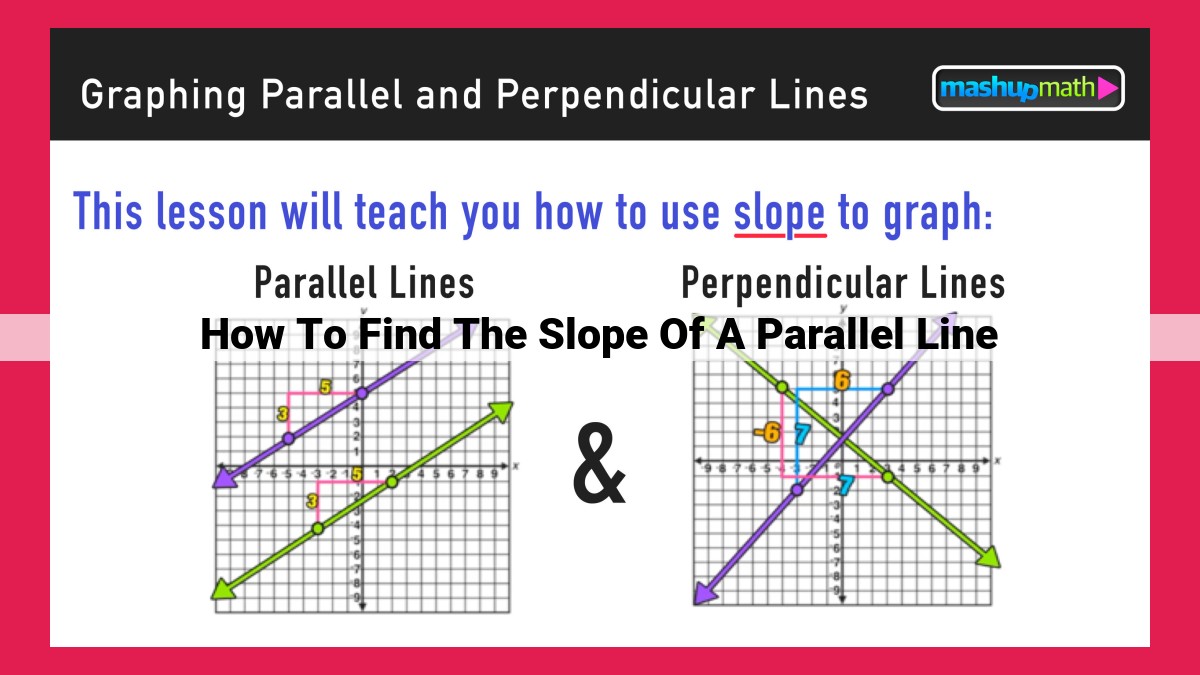
To find the slope of a line parallel to a given line, establish that parallel lines have identical slopes. Determine the slope of the given line using the slope formula: m = (y2 – y1) / (x2 – x1). The slope of the parallel line will be the same value as the slope of the given line. This is because parallel lines share the same angle of inclination, resulting in the same slope. Additionally, if the given line has an undefined slope (vertical), any parallel line will also have an undefined slope.

Understanding Parallelism

Imagine yourself driving down a long highway, with two lanes stretching out before you. As you travel, you notice that the lanes remain equidistant from each other, never crossing or diverging. These lanes are parallel — a fundamental concept in geometry that describes lines that maintain a constant distance.

The characteristics of parallel lines are equally fascinating. They lie on the same plane, never meeting or intersecting. This non-intersecting nature is what sets parallel lines apart from other line configurations.

One of the most significant relationships between parallel lines lies in their slopes. The slope measures the inclination of a line, or how steeply it rises or falls as you move along it. Remarkably, parallel lines share the same slope. This common slope is a crucial indicator of parallelism.

The Concept of Slope: A Geometrical Adventure into Line Inclination

In the realm of geometry, where lines dance before our eyes, the concept of slope plays a crucial role in understanding their orientation and behavior. Slope is a numerical value that measures the inclination of a line, revealing how it slants in the coordinate plane. It’s like a tiny compass, guiding us to unlock the secrets of parallel lines.

To grasp the essence of slope, imagine a line stretching across a terrain. Like a gentle breeze, the slope whispers the line’s angle of ascent or descent, telling us how much it rises or falls as it traverses the horizontal axis.

Mathematically, we express slope using a formula that has become a timeless treasure in the world of geometry: m = (y2 – y1) / (x2 – x1). This equation is the key that unlocks the slope’s numerical value, where:

• m represents the slope of the line.
• (y2 – y1) is the difference between the y-coordinates of two distinct points on the line.
• (x2 – x1) is the difference between the x-coordinates of those same two points.

Armed with this formula, we can embark on a quest to determine the slope of any line we encounter, opening doors to a deeper understanding of geometry and its captivating puzzles.

Slope of Parallel Lines: A Simple Explanation

In the realm of geometry, understanding the concept of parallelism is crucial. Parallel lines are those that never intersect, no matter how far they are extended. One of the key characteristics that defines parallel lines is their slope.

Slope is a measure of a line’s steepness or inclination. It is calculated using the following formula:

m = (y2 - y1) / (x2 - x1)

where:

• m represents the slope
• (x1, y1) and (x2, y2) are any two points on the line

Now, let’s delve into the relationship between parallel lines and their slopes. The fundamental fact to remember is that parallel lines have the same slope. This means that if you know the slope of one parallel line, you automatically know the slope of all other parallel lines.

This concept is particularly useful when you need to determine the slope of a parallel line without having direct access to it. For instance, imagine you have a line segment with a slope of 2. If you want to draw a parallel line that passes through a different point, simply use the same slope of 2.

It’s important to note that parallel lines can have undefined slopes. This occurs when the lines are vertical (i.e., perfectly straight up and down). In such cases, the slope formula results in an undefined value since the denominator (x2 - x1) becomes zero.

Understanding the slope of parallel lines is essential for various geometric applications. By recognizing that parallel lines have the same slope, you can solve problems related to line orientation, line intersections, and many other geometric concepts.

Parallel Lines and Slope: A Geometric Adventure

Understanding Parallelism: The Key to Geometric Harmony

In the realm of geometry, parallel lines hold a special place, characterized by their striking similarity. They run side by side, never meeting, like two ships sailing parallel courses across the vast ocean. Defining these lines, we uncover their unique characteristics: they share the same distance, never straying from each other, and they possess a constant angle of separation.

Delving into the Concept of Slope: Measuring the Line’s Inclination

Lines have a personality all their own, and a crucial aspect of this personality is their slope. Slope measures the line’s inclination, the angle it forms with the horizontal. Like a staircase, the slope determines how steeply the line ascends or descends. The slope formula, m = (y2 – y1) / (x2 – x1), serves as the key to unlocking this geometric attribute.

Slope’s Role in Parallel Lines: A Consistent Companion

Parallel lines, like twins separated at birth, share many traits, including the same slope. This fundamental property allows us to determine the slope of a parallel line if given the slope of one of its parallel companions. If we know the slope of line 1, we can confidently say that any parallel line 2 will have the same slope. This consistent slope serves as a guiding principle in understanding parallel lines.

Slope Formula for Parallel Lines: Decoding Geometric Relationships

The slope formula we encountered earlier plays a pivotal role in unraveling the mysteries of parallel lines. By substituting the coordinates of two points on the known parallel line, we can determine the slope. This slope value then becomes the guiding light for finding the slope of any other parallel line.

However, some parallel lines have a special secret: they possess undefined slopes. These lines run vertically, perpendicular to the horizontal, forming an angle of 90 degrees. In such cases, the slope formula yields an undefined value, signifying their vertical orientation.

Beyond Parallelism: Slope’s Significance in Geometry

Slope’s influence extends far beyond parallel lines. It plays a crucial role in understanding the orientation of lines, determining whether they are parallel, perpendicular, or at an angle. Perpendicular lines, for instance, have slopes that are negative reciprocals. This mathematical relationship highlights the contrasting directions of perpendicular lines, guiding us in our geometric explorations.

In the tapestry of geometry, understanding parallelism and slope is an essential thread. By unraveling the secrets of these geometric concepts, we gain a deeper appreciation for the intricate relationships that shape our mathematical world.

Parallel Lines and Slope: A Comprehensive Guide

Understanding Parallelism

In the realm of geometry, parallel lines dance across the plane side by side, never crossing paths. Parallel lines are defined by their unwavering distance apart, preserving their equidistance as they stretch towards infinity. An intrinsic characteristic of parallel lines lies in their slopes, a measure of their slant or inclination.

The Concept of Slope

Slope, denoted by the letter m, quantifies a line’s rise over its run, unveiling its angle of ascent or descent. The slope formula expresses this relationship mathematically: m = (y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2) are any two distinct points on the line.

Slope of Parallel Lines

A profound connection exists between parallel lines and their slopes: parallel lines have identical slopes. This immutable truth stems from the fact that parallel lines maintain the same angle relative to the horizontal, regardless of their starting or ending points. Thus, if the slope of one parallel line is known, the slopes of all other parallel lines can be effortlessly determined.

Slope Formula for Parallel Lines

The slope formula serves as a powerful tool for unraveling the slopes of parallel lines. Given the slope m of one parallel line, the slope m’ of any other parallel line can be found using the following formula: m’ = m. This equation underscores the equality of slopes among parallel lines, emphasizing their unwavering parallelism.

Additional Considerations

Perpendicular Lines: While parallelism focuses on lines maintaining equal orientation, perpendicular lines exhibit a contrasting behavior. When two lines intersect to form a right angle, they are said to be perpendicular. Intriguingly, the slopes of perpendicular lines are negative reciprocals of each other. This reciprocal relationship highlights the complementary nature of perpendicular lines, where one line’s rise compensates for the other line’s run, creating a perfect 90-degree angle.

Orientation: The slope of a line holds immense significance in understanding the orientation of parallel and perpendicular lines. Parallel lines, with their shared slope, exhibit a uniform slant, moving in tandem without deviating from their shared direction. Perpendicular lines, with their negative reciprocals of slopes, display a complementary slant, intersecting to form precise right angles. These slope relationships provide a vital key to deciphering the intricate dance of lines on the geometric plane.