How To Find The Equation Of A Line Parallel To A Given Line: A Step-By-Step Guide

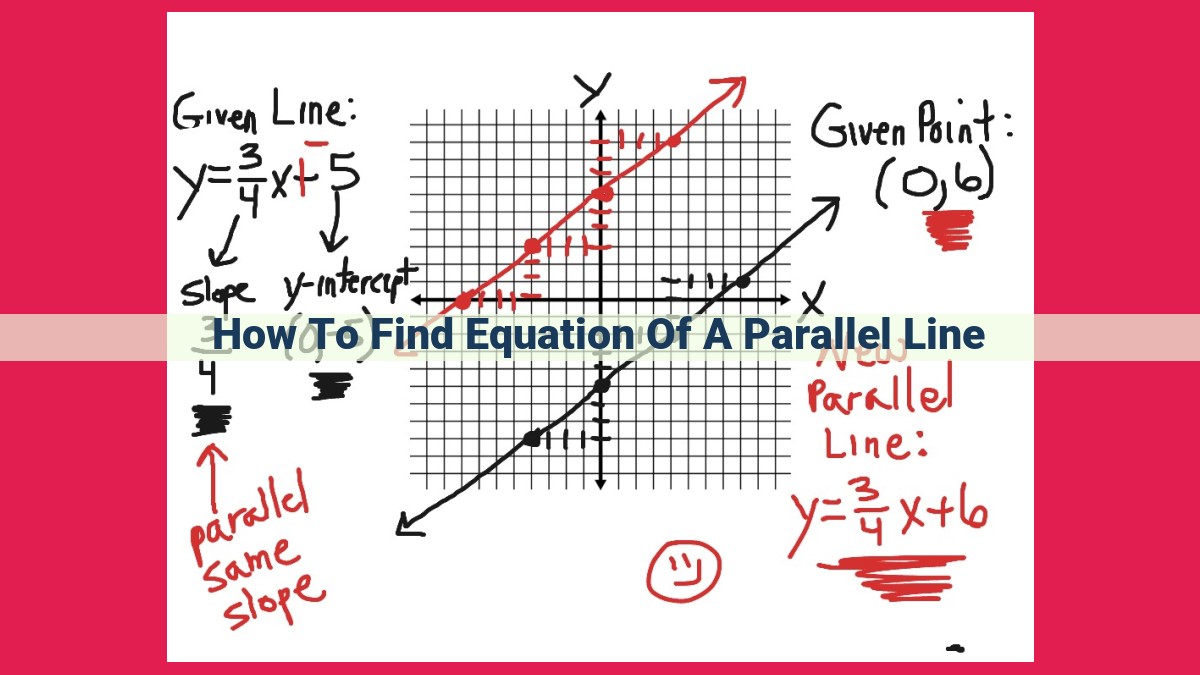
To find the equation of a line parallel to a given line, first determine the slope of the given line. Since parallel lines have the same slope, use the known slope to write the equation in point-slope form. Substitute the coordinates of a point on the parallel line into the point-slope form. Solve for the y-intercept (the value of b) to obtain the final equation of the parallel line in the slope-intercept form (y = mx + b).

Understanding Parallel Lines and Their Equations

When we embark on the mathematical journey of understanding lines, one pivotal concept we encounter is that of parallel lines. Parallel lines, by definition, are lines that never intersect and maintain an unwavering constant distance from each other. To comprehend the equation of a parallel line, we must first delve into the fundamental concept of slope.

Slope: The Inclination of a Line

Slope is the measure of a line’s inclination or steepness. It represents the ratio of the vertical change to the horizontal change along the line. By understanding slope, we can determine the direction and steepness of a line. Lines with a positive slope ascend from left to right, while lines with a negative slope descend. A zero slope indicates a horizontal line, and a slope of infinity corresponds to a vertical line.

Parallel Lines: Equal Slopes

The defining characteristic of parallel lines lies in their equal slopes. To understand this, we must first grasp the concept of intersecting lines, which cross each other at a single point. Perpendicular lines are a special case of intersecting lines where the lines meet at a right angle.

In contrast, parallel lines have the same slope but different y-intercepts. The y-intercept is the point where the line crosses the y-axis. This means that parallel lines share the same inclination or direction but differ in their vertical position. They run parallel to each other, never intersecting or crossing each other.

Importance of Slope for Parallel Lines

Understanding slope is crucial for finding the equation of a parallel line. Since parallel lines have equal slopes, the slope of the parallel line is the same as the slope of the given line. This knowledge enables us to derive the equation of the parallel line with ease.

Slope: The Measure of Inclination

Imagine a winding road snaking through a mountain landscape. As you drive along, you notice that the road is inclined, or tilted, from side to side. This inclination is a measure of how steep the road is. In mathematics, we refer to this inclination as the slope of a line.

Defining Slope

Slope is a fundamental concept in geometry and algebra. It measures the steepness or slant of a line. It is defined as the ratio of vertical change to horizontal change along the line.

To calculate the slope of a line, we take two points on the line, measure the vertical change, or rise, between them, and then divide it by the horizontal change, or run, between the same two points. The formula for slope is:

slope = (rise) / (run) = (y2 - y1) / (x2 - x1)

where (x1, y1) and (x2, y2) are the coordinates of the two points.

Slope and Angle

Slope is closely related to the angle that the line makes with the horizontal axis. A line with a steeper slope makes a larger angle with the horizontal, while a line with a smaller slope makes a smaller angle.

Negative, Positive, and Zero Slope

Slope can be positive, negative, or zero:

• A positive slope indicates that the line rises from left to right.
• A negative slope indicates that the line falls from left to right.
• A zero slope indicates that the line is horizontal and does not rise or fall.

Parallel Lines: A Journey Through Lines with Equal Slopes

In the realm of geometry, lines take center stage, revealing fascinating relationships that shape our understanding of shapes and spaces. When two lines embark on a journey of parallelism, they are destined to share a common trait – their slope, the measure of their inclination.

Parallel lines are like kindred spirits, their slopes harmoniously intertwined. They dance side by side, never destined to cross paths, their paths forever distinct. This unwavering parallelism has profound implications, painting a vivid picture of the geometric world.

Just as mountains share a similar gradient, parallel lines share a common slope. This shared inclination is their defining characteristic, the thread that binds them together. Unlike intersecting lines that embrace a collision course, parallel lines maintain their independence, forever parallel, forever apart.

In the tapestry of geometry, parallel lines play a pivotal role. They guide us in unraveling the mysteries of quadrilaterals, offering clues to the secrets of squares, rectangles, and parallelograms. Their presence is indispensable in the realm of symmetry, where their mirroring nature creates a sense of visual harmony.

Beyond the realm of geometry, parallel lines extend their influence into the practical world. They ensure the stable footing of bridges, guide the trajectories of airplanes, and serve as the foundation for architectural wonders. Their omnipresence underscores their multifaceted role in shaping our built environment.

As we delve deeper into the world of parallel lines, their characteristics and applications will continue to captivate and inspire. From the classroom to the construction site, their tale of parallelism unfolds, enriching our understanding of geometry and shaping the world around us.

Equation of a Line: Expressing Linear Relationships:

• Introduce the slope-intercept form (y = mx + b) and point-slope form (y – y1 = m(x – x1)).
• Explain the significance of the slope and y-intercept in each equation.

Equation of a Line: Expressing Linear Relationships

When exploring the world of mathematics, lines play a pivotal role in describing linear relationships. One crucial aspect of a line is its equation, which mathematically captures its path in the coordinate plane. Understanding how to write the equation of a line, particularly in the context of parallel lines, is essential for solving various mathematical problems.

Slope-Intercept Form

The *slope-intercept form is the most commonly used equation for a line. It takes the format y = mx + b, where:
* y represents the vertical (or y) coordinate of a point on the line.
* x is the horizontal (or x) coordinate of the point.
* m is the slope of the line, which measures its angle of inclination. It is calculated as the ratio of vertical change to horizontal change.
* b is the y-intercept of the line, which indicates the point where it intersects the y-axis (when x = 0).

Point-Slope Form

The *point-slope form is an alternative way to express the equation of a line. It is useful when we know a point on the line and its slope. The point-slope form is: y – y1 = m(x – x1), where:
* (x1, y1) is a known point on the line.
* m is the slope of the line.

Significance of Slope and Y-Intercept

The slope is a crucial factor in determining the line’s orientation. A positive slope indicates an upward slope, while a negative slope represents a downward slope. A zero slope represents a horizontal line, and a slope of infinity signifies a vertical line.

The y-intercept, on the other hand, indicates where the line crosses the y-axis. It provides valuable information about the line’s position relative to the origin.

Using Substitution to Find Parallel Lines

When working with parallel lines, a particularly intriguing aspect is their shared slope. Parallel lines by definition have the same slope, but different y-intercepts. Given a point on one parallel line and the slope of both lines, we can use substitution to derive the equation of the other parallel line.

First substitute the given point coordinates and the shared slope into the point-slope form.
Then solve for the y-intercept (b).
Finally construct the equation of the parallel line using the slope-intercept form: y = mx + b.

Y-Intercept: Where the Line Meets the Y-Axis

In the world of lines, there lies a special point known as the y-intercept, where the line intersects the y-axis. This point holds significance not only in defining the line’s position but also in understanding its relationship with the origin and axis of symmetry.

The y-axis, in its vertical splendor, serves as the boundary between positive and negative values. When a line crosses this axis, it marks the exact location where the line meets the y-axis. This point, where the value of x is zero, is known as the y-intercept.

The y-intercept tells us exactly how far the line is from the origin, the point where both the x-axis and y-axis meet. A positive y-intercept indicates that the line crosses the y-axis above the origin, while a negative y-intercept means it crosses below.

Furthermore, the y-intercept plays a crucial role in determining the axis of symmetry of the line. For linear lines, the axis of symmetry is a vertical line that divides the line into two mirror images. The axis of symmetry is located exactly halfway between the x-intercepts, which are the points where the line crosses the x-axis.

The y-intercept also provides insight into the line’s overall shape. Lines with a positive y-intercept slope upwards as they move from left to right, while those with a negative y-intercept slope downwards. By understanding the y-intercept, we can quickly visualize the orientation of the line in the coordinate plane.

In conclusion, the y-intercept is a vital point that defines a line’s position, relationship with the origin, and axis of symmetry. Its significance lies in providing a clear understanding of the line’s behavior and appearance in the world of geometry.

Point-Slope Form: The Key to Writing Equations for Parallel Lines

In the realm of geometry, we often encounter parallel lines, lines that run side by side forever without ever intersecting. The key to understanding parallel lines lies in their slopes. Slope, a measure of a line’s inclination, determines the direction in which it travels.

When two lines have the same slope, they are considered parallel. This concept is crucial in finding the equation of a line parallel to another. The point-slope form provides a powerful tool for constructing such equations.

To derive the point-slope form, let’s consider the slope-intercept form of a linear equation: y = mx + b. Here, m represents the slope, and b is the y-intercept, the point where the line crosses the y-axis.

Now, let’s take a specific point (x1, y1) on a line. Using the slope m, we can determine the slope of any line that passes through this point. The point-slope form is derived by solving for y in the slope-intercept form and substituting y1 and x1 for y and x, respectively:

y - y1 = m(x - x1)

This equation, the point-slope form, allows us to write the equation of a line given a point on the line and its slope. To find the equation of a line parallel to a given line, simply substitute the slope of the given line into the point-slope form and use a point on the parallel line.

By solving for y-intercept, we get the equation of the parallel line:

y = mx + (y1 - mx1)

Using the point-slope form and substitution, we can effortlessly find the equations of lines parallel to any given line. This concept is extensively applied in various domains of mathematics and science, helping us unravel the secrets of geometry and beyond.

Finding the Equation of a Parallel Line: A Step-by-Step Guide

When it comes to lines in mathematics, understanding parallelism is crucial. Parallel lines run alongside each other, never crossing paths, and they share a common characteristic: equal slopes.

Step 1: Substituting a Point on the Parallel Line

Imagine you have two parallel lines, l and m. You know a point (x1, y1) lies on line m. To find the equation of line m, substitute this point into the point-slope form:

y - y1 = m(x - x1)

Step 2: Solving for the Y-Intercept

The y-intercept is the point where the line intersects the y-axis. To solve for it, let x = 0 in the equation:

y - y1 = m(0 - x1)
y - y1 = -mx1
y = y1 - mx1

This gives you the y-intercept of the parallel line, (0, y1 – mx1).

Step 3: Writing the Equation of the Parallel Line

Now, use the slope-intercept form:

y = mx + b

Replace m with the slope and b with the y-intercept you found:

y = mx + (y1 - mx1)

This is the equation of the parallel line m, passing through the point (x1, y1) and having the same slope as line l.