Finding The Base Of A Parallelogram For Optimal Seo Performance
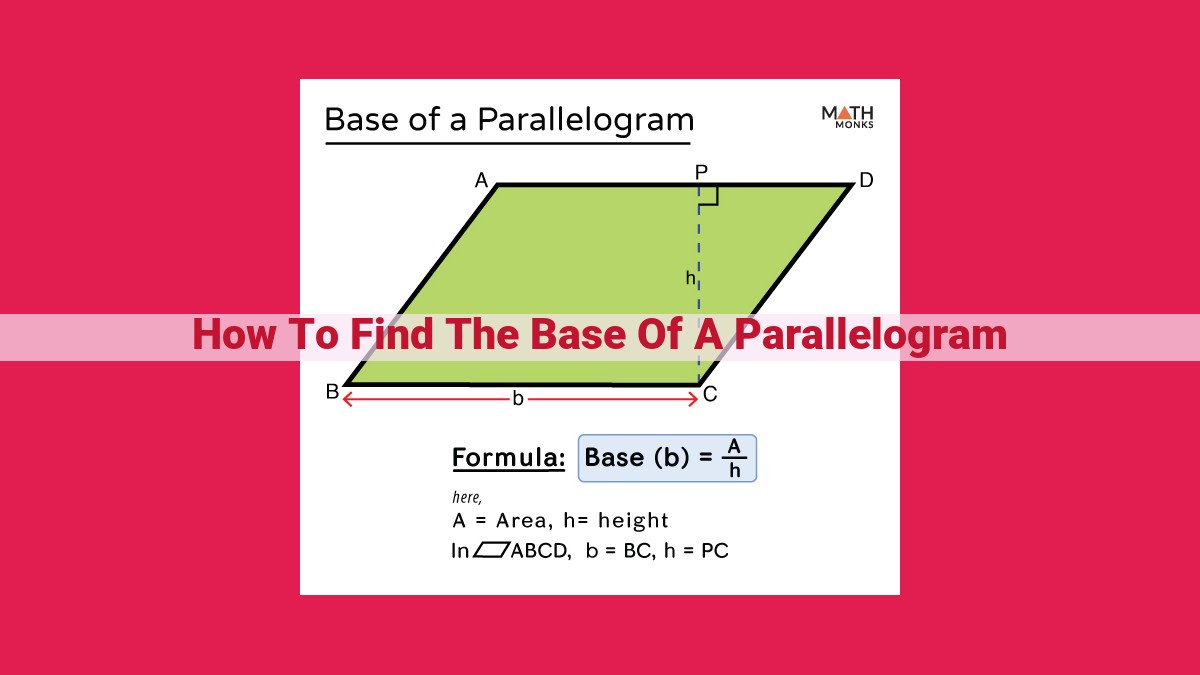
To find the base of a parallelogram, first understand its parallel sides. A parallelogram has two pairs of parallel sides. The base is one of the two parallel sides. The area of a parallelogram is calculated using the formula A = b * h, where ‘b’ is the base and ‘h’ is the height. To find the base, rearrange the formula to b = A / h. Determine the area of the parallelogram and divide it by the height to get the base length. For example, if the area is 24 square units and the height is 6 units, the base will be 4 units.
Understanding Parallelograms
- Definition of a parallelogram, including its parallel sides.
Understanding Parallelograms: Exploring a Geometric Quadrilateral
In the realm of geometry, where shapes dance and angles converge, lies a fascinating figure known as a parallelogram. Parallelograms, distinguished by their captivating parallel sides, have a rich history and practical applications that make them an integral part of our world.
Definition of a Parallelogram
A parallelogram is a quadrilateral, a figure with four sides. Its defining characteristic lies in its parallel sides, which run alongside each other without ever intersecting. When we draw a parallelogram on paper, we can observe two pairs of parallel lines forming the sides of the shape.
Parallel Sides: A Key Feature
The parallel sides of a parallelogram are equal in length and opposite to each other. This unique property gives parallelograms their distinctive shape and many of their interesting geometric properties.
Role in Architecture and Design
Parallelograms play a vital role in architecture and design, where their strong and stable structure makes them ideal for creating buildings, bridges, and other structures. Their parallel sides ensure uniformity and balance, while their equal opposite sides provide symmetry and aesthetics.
Understanding Base and Height of a Parallelogram
A parallelogram, distinguished by its parallel sides and opposite congruent angles, possesses a well-defined base and height. The base represents the horizontal side of the parallelogram, while the height stands perpendicular to the base, measuring the distance between the base and the opposite side.
In the context of a parallelogram, the base and height are crucial dimensions that play a pivotal role in calculating the parallelogram’s area. By understanding the concepts of base and height, we unlock the ability to efficiently determine the area of any parallelogram.
Area Formula
- Formula for calculating the area of a parallelogram (A = b * h).
Unveiling the Secret of Parallelograms: Area and Beyond
In the realm of geometry, parallelograms stand out with their unique shape, characterized by parallel sides. These fascinating figures possess a rich mathematical tapestry, and one of its most fundamental aspects is their area.
Area Formula: A Simple Yet Powerful Tool
Just like any other shape, parallelograms have a specific formula that allows us to calculate their area. It’s an equation that holds the key to unlocking the surface measure of these intriguing quadrilaterals. The formula for the area of a parallelogram is simply:
A = b * h
Where:
* A represents the area of the parallelogram
* b denotes the length of the base (one of the parallel sides)
* h represents the height (the perpendicular distance between the base and the opposite parallel side)
This formula is not just a random mathematical equation; it’s a testament to the fundamental properties of parallelograms. It embodies the concept that the area of a parallelogram is determined by the product of its base and height.
Unveiling the Hidden Beauty: Understanding Base and Height
The base and height are two crucial dimensions that play a pivotal role in the area calculation. The base is the length of one of the parallel sides, and the height is the perpendicular distance from any side to another parallel side. Together, they form the essential building blocks for determining the surface area of a parallelogram.
A Solveable Enigma: Finding the Base Using the Formula
Sometimes, we may know the area of a parallelogram and its height but not its base. That’s where the magic of algebra comes into play. By rearranging the area formula, we can derive an equation that allows us to find the base:
b = A / h
Using this formula, we can effortlessly determine the elusive base, unlocking the complete picture of the parallelogram’s dimensions.
A Glimpse into Action: An Illustrative Example
To solidify our understanding, let’s delve into a practical example. Suppose we have a parallelogram with an area of 48 square units and a height of 6 units. Armed with the formula b = A / h, we can find the length of its base:
b = 48 / 6 = 8 units
And there you have it! The base of the parallelogram is 8 units. This example highlights the power of the area formula and its ability to unveil the secrets hidden within a parallelogram’s shape.
Finding the Base of a Parallelogram Using the Area Formula
In the realm of geometry, parallelograms reign supreme as intriguing shapes with their distinctive parallel sides. These fascinating figures possess a unique charm, and understanding their properties is essential for navigating the world of shapes. One intriguing aspect of parallelograms is their base, which plays a pivotal role in determining their area.
To unveil the secrets of the parallelogram’s base, let’s embark on a mathematical adventure. We begin with the fundamental area formula for a parallelogram:
A = b * h
Where:
- A represents the area of the parallelogram
- b represents the base of the parallelogram
- h represents the height of the parallelogram
This formula serves as our guide in our quest to find the elusive base. However, challenges await us, for the formula assumes we know the base, which is precisely what we seek. So, how do we navigate this conundrum?
Fear not, for a clever strategy awaits us. By rearranging the formula, we can isolate the base as the unknown variable:
b = A / h
This revised formula empowers us to determine the base once we have the area and height at our disposal. It’s a tool that unlocks the mysteries of parallelogram bases, allowing us to conquer any geometric challenge that comes our way.
Understanding Parallelograms and Their Area
Defining Parallelograms and Their Unique Features
A parallelogram is a quadrilateral shape with parallel opposite sides. This means that the two pairs of sides run alongside each other, forming equal and opposite angles at each vertex. Parallelograms are characterized by their unique property of having opposite sides of equal length and opposite angles of equal measure.
Base, Height, and the Area Formula
Within a parallelogram, the base is typically denoted as the horizontal or bottom side, and the height represents the perpendicular distance from the base to the opposite side. Together, these two measurements are crucial in determining the area of the parallelogram.
The area formula for a parallelogram is A = b * h, where A represents the area, b is the base, and h is the height. This formula highlights the correlation between the area and the product of the base and height.
Finding the Base Using the Area Formula
If you’re faced with a scenario where you know the area and height of a parallelogram, you can use the area formula to determine the base. Here are the steps involved:
- Start with the area formula: A = b * h
- Isolate the base (b) by dividing the area (A) by the height (h).
- This gives you the formula: b = A / h
Example: Calculating the Base
Let’s put this concept into practice with an example. Suppose you have a parallelogram with an area of 24 square units and a height of 4 units. Using the formula b = A / h, we can find the base:
- b = 24 / 4
- b = 6
Therefore, the base of the parallelogram is 6 units.