Exponential Vs. Logistic Growth: Understanding Population Dynamics In Diverse Environments

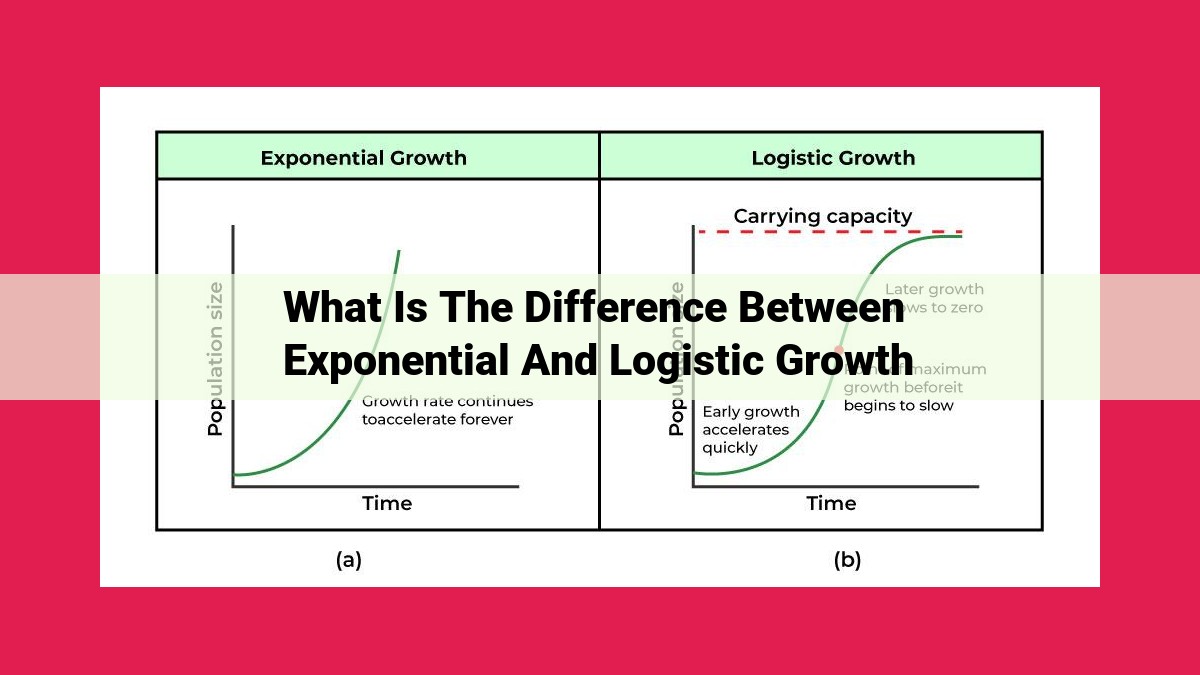
Exponential growth exhibits a constant percentage increase, leading to rapid population expansion, while logistic growth accounts for environmental limitations by introducing a carrying capacity, resulting in a more realistic representation of population growth. Exponential growth lacks an upper limit but has a higher initial growth rate, while logistic growth reaches a plateau due to carrying capacity. Both models have important applications, with exponential growth describing bacterial growth and radioactive decay, while logistic growth predicts population growth in limited environments and resource depletion.

Understanding Population Growth Models: Essential Tools for Various Fields

In the realm of scientific modeling, population growth models play a pivotal role in comprehending the dynamics of living organisms and their interactions with their environment. These models underpin a wide range of disciplines, including ecology, epidemiology, and resource management, empowering scientists to unravel complex patterns and make informed predictions.

Exponential Growth: A Surge in Numbers

Exponential growth, characterized by a constant percentage rate of increase, is often observed in situations where there are abundant resources and little competition. Think of a thriving bacterial colony or the spread of a rumor through a tightly connected network. As the population size increases, so does the rate of growth, leading to an exponential surge. However, this relentless expansion cannot persist indefinitely.

Logistic Growth: A Realistic Perspective

In contrast to exponential growth, logistic growth incorporates the concept of carrying capacity—the maximum population size that an environment can sustain. This model recognizes the interplay between population growth and resource constraints. Initially, a population may experience a lag phase, followed by a period of exponential growth. However, as resources become limited, the growth rate slows down, eventually reaching a stationary phase where the population size stabilizes around the carrying capacity.

Key Differences: A Comparative Analysis

Exponential and logistic growth models differ in several fundamental ways. Exponential growth exhibits an unbounded increase, while logistic growth has an upper limit determined by the carrying capacity. Exponential decay, the inverse of exponential growth, also contrasts with logistic growth, which depicts a gradual leveling off.

Applications in the Real World

Exponential growth models have found wide applicability in diverse fields. Biologists utilize them to understand the growth of bacterial populations, while physicists employ them to model the decay of radioactive isotopes. Logistic growth models are crucial for ecologists studying animal populations and predicting how resource limitations affect their dynamics.

Population growth models provide indispensable tools for scientists to unravel the complexities of living systems and predict future outcomes. Exponential and logistic growth models, with their unique characteristics and applications, serve as cornerstones in ecological studies, epidemiological modeling, and resource management. Understanding these concepts empowers us to make informed decisions and devise strategies to ensure the sustainability of life on Earth.

Exponential Growth: A Tale of Unchecked Expansion

Imagine a small forest nestled in a secluded valley. Its trees, thriving in the sunlight, grow taller and more numerous with each passing year. This steady increase, described by exponential growth, is a fundamental pattern observed in nature and beyond.

Defining Exponential Growth

Exponential growth occurs when a quantity grows at a constant percentage rate over time. The key characteristic of exponential growth is the consistent ratio between the change in quantity and the original quantity. This ratio is known as the growth rate.

Implications of Exponential Growth

The constant growth rate in exponential growth leads to rapid acceleration.

• Growth rate > 1: The quantity increases at an ever-increasing rate, leading to exponential expansion.
• Growth rate = 1: The quantity grows linearly, at a steady rate.
• Growth rate < 1: The quantity decreases exponentially, approaching zero over time.

Example: Bacterial Growth

Bacteria, tiny living organisms, are a classic example of exponential growth. When bacteria reproduce, they create identical copies of themselves, leading to a doubling of the population over a specific time interval. In a petri dish, bacteria can multiply at an astonishing rate, quickly covering the entire surface.

Implications of Exponential Decay

Exponential growth can also be applied to situations where a quantity decreases over time. Known as exponential decay, it occurs when the growth rate is less than 1.

• Radioactive isotopes lose their radioactivity over time at a constant percentage rate.
• Evaporation removes water from a puddle at a constant fractional rate.

Exponential growth and decay are powerful mathematical tools that describe the behavior of many natural and artificial systems. Understanding these concepts is crucial in fields such as ecology, epidemiology, and resource management. By unraveling the mysteries of exponential growth, we gain valuable insights into the dynamics of our world.

Logistic Growth: A More Realistic Population Growth Model

In the realm of population growth, exponential growth often sets the stage, characterized by an unbridled multiplication. However, reality often dictates a different story. Logistic growth emerges as a more nuanced and realistic model, acknowledging the environmental constraints that shape the trajectory of any population.

Unlike exponential growth, logistic growth recognizes that carrying capacity, the maximum population size an environment can sustain, plays a pivotal role. The carrying capacity represents the equilibrium point where resources and space become limiting factors, taming the relentless expansion of a population.

The logistic growth curve depicts a characteristic three-phase journey. The lag phase marks the initial period of population growth, where the population size remains relatively small, gathering momentum. This phase is characterized by low birth rates and high death rates.

As the population size increases, it enters the exponential phase, a period of rapid growth. Birth rates soar, while death rates decline, leading to a surge in population size. However, this exponential expansion cannot continue indefinitely.

Eventually, the population encounters the carrying capacity and enters the stationary phase. Birth rates and death rates equalize, and the population size stabilizes around the carrying capacity. This equilibrium represents a sustainable balance between population growth and environmental constraints.

Understanding logistic growth is crucial in fields such as ecology, epidemiology, and resource management. It provides insights into how populations adapt to limited resources and how environmental factors influence population dynamics. By modeling population growth using logistic functions, scientists and policymakers can predict population trends, manage resources sustainably, and anticipate the challenges associated with population growth in a finite world.

Exponential vs. Logistic Growth: Key Differences

Imagine two flourishing plant populations: one basking in the sun’s warmth, with ample space and resources, and the other struggling to survive in a crowded and limited environment. These two scenarios aptly illustrate the contrasting tales of exponential and logistic growth models.

Exponential Growth:

• Characterized by a constant percentage rate of increase
• Population size grows rapidly, unbound by external constraints
• Typical of environments with abundant resources and no limitations on growth potential
• Often seen in rapidly reproducing organisms or early stages of population growth

Logistic Growth:

• Incorporates environmental constraints that limit population growth
• Carrying capacity represents the maximum population size that can be sustained by the available resources
• Initially exhibits exponential growth, but slows down as it approaches carrying capacity
• Features distinct phases: lag phase, exponential phase, and stationary phase

Key Differences:

• Growth Pattern: Exponential growth is unbounded, while logistic growth slows down as it approaches carrying capacity.
• Upper Limit: Exponential growth has no upper limit, while logistic growth is capped by carrying capacity.
• Environmental Impact: Exponential growth does not consider environmental constraints, while logistic growth models the effects of resource availability.

In essence, exponential growth assumes unlimited resources and leads to unsustainable population increases. On the other hand, logistic growth acknowledges environmental limitations and predicts a more realistic population trajectory. Understanding these key differences is crucial for accurate modeling in fields such as ecology, epidemiology, and resource management.

Applications of Exponential and Logistic Growth

Exponential Growth: A Tale of Unchecked Expansion

Imagine a rapidly growing colony of bacteria. Each bacterium divides every twenty minutes, doubling its population. This is exponential growth at its peak, where the rate of increase is proportional to the current population. Such growth can be observed in various scenarios, including the spread of infectious diseases or the escalating decay of radioactive substances.

Logistic Growth: A Realistic Adaptation to Environmental Limits

However, in most real-world situations, growth is not unchecked. Resources become有限, and the environment poses constraints. Logistic growth captures this reality. As a population grows, it reaches a point of equilibrium, known as the carrying capacity. Beyond this point, growth slows and eventually stabilizes.

Logistic growth models have practical applications in predicting population growth in limited environments. Ecologists use these models to forecast the dynamics of animal populations, while epidemiologists predict the spread of diseases in constrained settings. For example, logisticians may help estimate the number of individuals who will contract a contagious disease in a defined community, taking into account factors like immunity and vaccination rates.

Additionally, logistic growth can also be used to model resource depletion. As resources become scarce, the growth of the population that relies on those resources slows and eventually plateaus. Understanding these growth patterns is critical for sustainable resource management and conservation efforts.