Understanding Event Relationships In Probability: Disjoint, Independent, And Marginal Independence

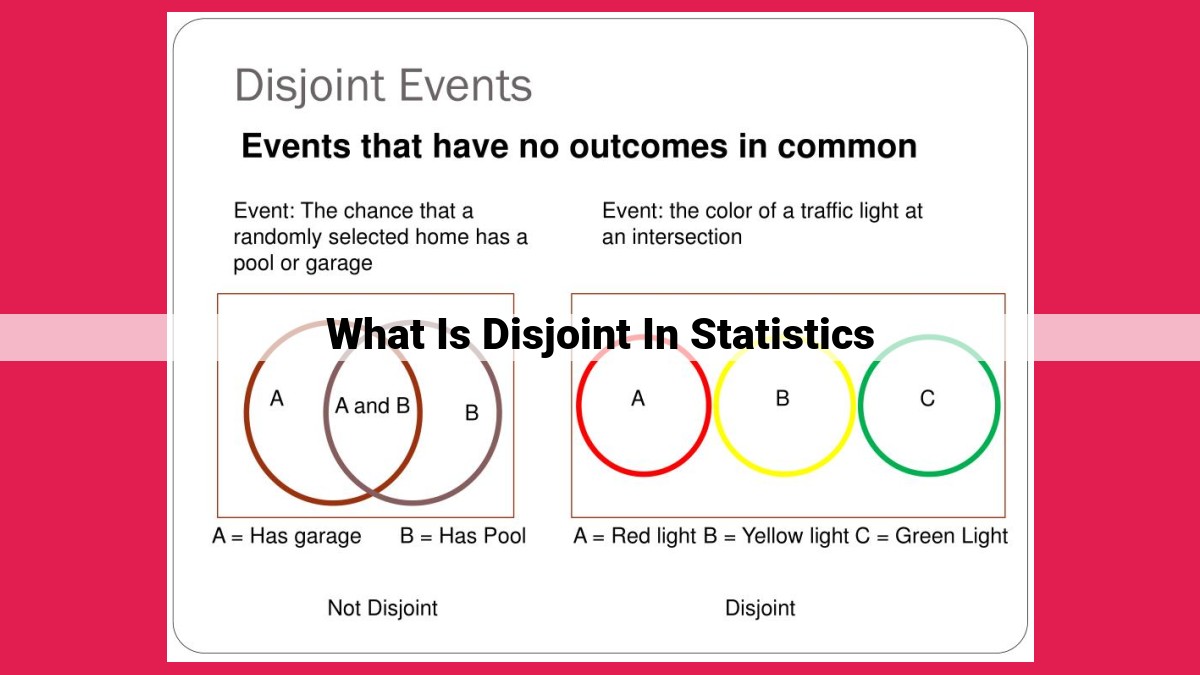
Disjoint events are mutually exclusive events that cannot occur simultaneously, unlike mutually exclusive events that may overlap. Independent events have no influence on each other’s probability, while conditionally independent events are independent given a certain condition. Marginal independence occurs when events are independent when considered together but may be conditionally dependent. Disjoint events are used in statistical analysis to calculate probabilities accurately, understanding the behavior of random variables and making inferences in decision-making processes.

• Define disjoint events as mutually exclusive events that cannot occur simultaneously.

Understanding Disjoint Events: Events that Never Crisscross

Disjoint events, like two parallel lines that never meet, are mutually exclusive events that cannot occur at the same time. In the realm of probability, they’re like the opposite of twins that share everything – they’re individuals with distinct identities.

For instance, let’s say you’re flipping a coin. You can either get heads or tails, but never both at once. These outcomes are disjoint events because they’re mutually exclusive: it’s impossible to flip heads and tails simultaneously.

Disjoint vs. Mutually Exclusive Events: Unraveling the Overlap

In the realm of probability theory, events play a central role in describing the likelihood of outcomes. Among these events, disjoint and mutually exclusive events hold a special place. While often used interchangeably, these terms have distinct nuances that shape their mathematical properties and applications.

Disjoint Events: Absolute Exclusivity

Disjoint events are a type of mutually exclusive events that possess a unique characteristic: they cannot occur simultaneously. Imagine flipping a coin. The event of getting heads and the event of getting tails are disjoint events. It’s impossible for both outcomes to occur on the same coin flip.

Mutually Exclusive Events: Overlapping Barriers

Mutually exclusive events are a broader category that includes disjoint events. They represent events that cannot happen jointly, but the possibility of their individual occurrences remains. For instance, consider rolling a six-sided dice. The event of getting a 2 and the event of getting a 4 are mutually exclusive. While these outcomes can’t happen simultaneously, both outcomes are still possible on a single dice roll.

The Interplay of Disjoint and Mutually Exclusive

The relationship between disjoint and mutually exclusive events can be visualized as nested sets. Disjoint events form a subset of mutually exclusive events. In other words, every disjoint event is also a mutually exclusive event, but not all mutually exclusive events are disjoint.

Applications in Probability Calculations

Understanding the distinction between disjoint and mutually exclusive events is crucial for probability calculations. In the case of disjoint events, the probability of their joint occurrence is always zero. This means that if two events are disjoint, the probability of either event occurring is equal to the probability of that event occurring alone.

On the other hand, for mutually exclusive events but not disjoint, the probability of their joint occurrence is positive. This is because there’s a non-zero probability that one of the events will occur. The total probability of the mutually exclusive events is the sum of their individual probabilities.

Disjoint and mutually exclusive events are fundamental concepts in probability theory. Disjoint events represent an extreme case of mutual exclusivity where the events are completely incompatible, while mutually exclusive events allow for individual occurrences but prohibit joint outcomes. Understanding these distinctions is essential for accurate probability calculations and a deeper understanding of the interplay of events in statistical analysis.

Independent Events: Unraveling the Connection between Probability and Happenstance

Let’s embark on a captivating journey into the fascinating world of probability theory, where we’ll explore the enigmatic concept of independent events. These enigmatic occurrences are like two distant stars, their fates unrelated, each shining brightly in its cosmic realm. Unlike their disjoint counterparts, which resemble two opposing sides of a coin, independent events have no inherent connection; they can coexist harmoniously without influencing each other’s existence.

The concept of probability, the enigmatic force that governs the likelihood of events, plays a pivotal role in understanding independent events. Probability, like a mystical oracle, assigns a numerical value to each event, representing its chance of occurrence. When we speak of independent events, we enter a realm where these probabilities remain unaffected by the occurrence or non-occurrence of any other event.

Consider a simple example: imagine a fair coin toss. Each flip of the coin is an independent event, meaning the outcome of one flip has no bearing on the next. The probability of obtaining heads or tails remains constant regardless of the previous outcomes. This independence allows us to calculate the probability of a specific sequence of events by simply multiplying the individual probabilities.

The world of independent events extends far beyond coin tosses; it permeates various aspects of our lives. From the probability of rolling a specific number on a dice to the likelihood of a particular weather pattern, independent events are the building blocks of many statistical models. Understanding their behavior helps us make informed decisions based on the probabilities of future occurrences.

Conditional Independence: Unveiling the Interplay of Events

In the realm of probability theory, events play a pivotal role, and their relationships can often be complex and intriguing. Conditional independence is one such concept that offers a nuanced understanding of how events might be intertwined.

Independent Events vs. Conditional Independence

Independent events are those whose occurrences do not influence each other. For instance, the outcome of flipping a coin twice does not affect the outcome of the second flip. However, conditional independence introduces a new dimension to the equation. Two events, A and B, are conditionally independent given a third event, C, if the occurrence of C renders the probability of A independent of the occurrence of B.

Scenarios of Conditional Independence

Conditional independence is often encountered in scenarios where events are initially dependent but become independent when a specific condition is imposed. For example, consider two events: rolling a six on a die and drawing a heart from a deck of cards. These events are usually dependent, but if we condition on the event of selecting a red card from the deck, the probability of rolling a six becomes unaffected by the outcome of the heart draw.

Marrying Conditional and Marginal Independence

Marginal independence is a broader concept that encompasses conditional independence. Events A and B are marginally independent if they are independent for any possible value of C. In other words, the occurrence of C does not alter the independence of A and B. However, it’s important to note that marginal independence does not imply conditional independence.

Marginal Independence: Unveiling the Relationship between Conditional Independence and Event Interactions

In the realm of probability theory, understanding event interactions is crucial. Marginal independence, a concept closely related to conditional independence, provides valuable insights into the behavior of events under specific conditions.

Conditional independence occurs when the probability of one event is unaffected by the occurrence of another event, given the knowledge of a third event. In other words, the events are independent within the context of the third event. However, this interdependence may change when the third event is no longer considered.

Marginal independence, on the other hand, occurs when two events are independent regardless of any additional information or conditions. It implies that the probability of one event is not influenced by the occurrence of the other, even when no other factors are taken into account.

Conditions for Marginal Independence:

• Two events, A and B, are marginally independent if and only if they are independent unconditionally.
• If A and B are conditionally independent given a third event C, but not unconditionally, then they are not marginally independent.

In essence, marginal independence signifies a fundamental disconnect between the probabilities of events. It suggests that the events do not interact or influence each other in any way, even when viewed from different perspectives or under varying conditions. This concept plays a significant role in probability calculations and statistical analysis, allowing researchers to make accurate deductions about event occurrences.

Applications of Disjoint Events in Statistical Analysis

Disjoint events, being mutually exclusive, play a crucial role in statistical analysis. Consider this scenario: You’re rolling a fair six-sided die, and you want to know the probability of rolling a number greater than 4. In this case, the events are disjoint because you can’t roll a number greater than 4 and a number less than or equal to 4 simultaneously. This disjoint nature allows us to calculate the probability accurately.

The probability of rolling a number greater than 4 is the sum of the probabilities of rolling 5 or 6. Since these events are disjoint, we can simply add their probabilities: P(rolling a number greater than 4) = P(rolling 5) + P(rolling 6) = 1/3 + 1/6 = 1/2.

Understanding disjoint events is also essential for avoiding overcounting or double-counting in probability calculations. Imagine you’re drawing two balls from a bag containing three red balls and two blue balls. The event of drawing a red ball on the first draw is disjoint from the event of drawing a red ball on the second draw. If we didn’t consider this, we would overestimate the probability of drawing two red balls.

In summary, disjoint events are essential for accurate probability calculations. They prevent overcounting and provide a clear understanding of the relationship between mutually exclusive events. In statistical analysis, disjoint events are used in various applications, such as calculating probabilities, sampling, and hypothesis testing.