Mastering Equation Solving: A Guide To Uncovering Hidden Solutions
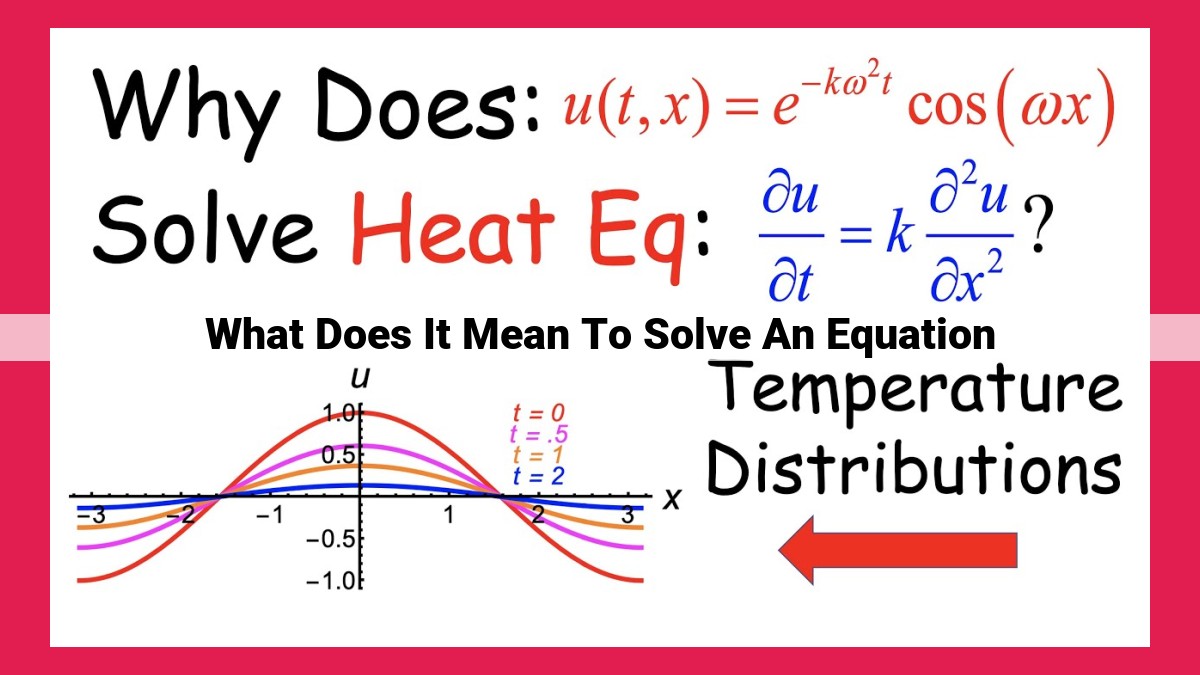
Equation solving involves finding the values that make an equation true, known as solutions. It requires manipulating the equation using properties of equality, including the distributive property, inverse operations, and order of operations. By isolating the variable on one side of the equation, we can determine the solution(s). Solving equations unlocks their value in mathematical and real-world applications, from solving for dimensions to predicting outcomes.
Equation Solving: Delving into the Art of Finding Solutions
In the tapestry of mathematics, equation solving stands as a fundamental skill, akin to a key that unlocks the secrets of the numerical realm. It is the process of finding the value of a variable that transforms an equation from a mere expression into a statement of truth. Equations pervade our mathematical journey, from the simplest of algebraic expressions to the most complex of scientific formulas.
The significance of equation solving extends far beyond the classroom. It empowers us to understand the world around us, from calculating the trajectory of a projectile to forecasting the weather. Whether we are engineers designing bridges, scientists unraveling the mysteries of the universe, or simply managing our finances, solving equations is an indispensable tool that guides our decisions and illuminates our path.
**Key Concepts in Equation Solving: A Journey to Find the X**
When diving into the world of equations, understanding the crucial concepts that guide the journey towards finding their solutions becomes paramount. These concepts are the foundation upon which equation-solving prowess is built.
Solutions: The Holy Grail of Equations
At the heart of every equation lies the quest for its solutions – those elusive values that make the equation true. These solutions can manifest in various guises, such as identities, contradictions, and even no solutions at all.
Identities: A Symphony of Truth
An identity stands tall as an equation that holds true for any value of its variable. It’s like a harmonious melody that remains consistent, no matter the note you play. Identities are the epitome of solvability, as they always possess an infinite number of solutions.
Contradictions: The Enigma of Falsity
Contradictions, on the other hand, are equations that stumble upon an unsolvable fate – they remain false for all values of their variable. These enigmatic equations serve as sentinels, guarding the realm of unsolvable puzzles.
Substitution: The Art of Disguise
Substitution, the sorcerer’s trick of equations, allows us to transform equations by replacing one variable with another or even an entire expression. It’s a powerful tool that reshapes equations, paving the path for their solutions.
Isolation: The Ultimate Revelation
Isolation, the final key, unravels the mystery of the variable. It’s the process of moving the variable to one side of the equation, leaving us with its true value revealed. Isolation is the triumphant moment when the unknown is unveiled.
These concepts, like threads woven together, form the tapestry of equation solving. They guide us through the labyrinth of equations, helping us unravel their secrets and conquer the challenges they present.
Understanding the Powerful Tools of Equality for Equation Solving
In the realm of mathematics, solving equations is akin to unlocking the mysteries of a puzzle. It’s a process that unravels the unknown, revealing the values that make an equation stand true. To conquer this mathematical adventure, we must equip ourselves with the fundamental properties of equality—the tools that empower us to transform and simplify equations, ultimately leading us to the elusive solutions.
The Distributive Property: Multiplying with Ease
Imagine an equation like 3(x + 2) = 15. To solve for x, we must distribute the 3 to the terms within the parentheses. The distributive property allows us to do this with ease, multiplying 3 by both x and 2. This transforms the equation into 3x + 6 = 15, bringing us one step closer to our goal.
Inverse Operations: Undoing Mathematical Moves
Inverse operations are the Ying and Yang of the mathematical world. They undo each other’s effects, like the addition and subtraction or multiplication and division. To isolate a variable, we use inverse operations like moving constants to the other side of the equation. For example, to solve for y in the equation y – 5 = 10, we add 5 to both sides, effectively undoing the subtraction.
Order of Operations: A Mathematical Symphony
Think of solving equations as a symphony, where each operation plays a specific role and order matters. The order of operations—known as PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction)—guides us on which operations to perform first. Ignoring this order can lead to incorrect solutions, like a conductor mixing up the sequence of instruments in an orchestra.