Unveiling The Elliptical Paths Of Planets: An Exploration Of Orbital Eccentricity And Axis Dimensions

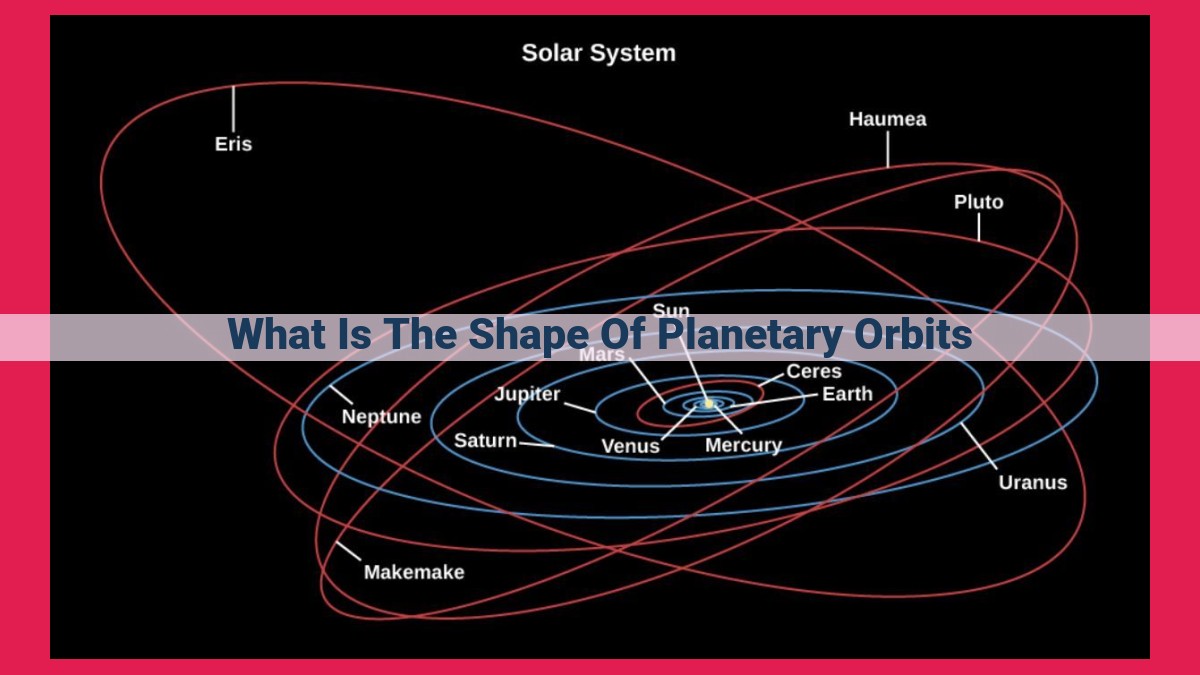
Planetary orbits, governed by gravitational forces, exhibit diverse shapes known as ellipses. These elliptical paths are characterized by an eccentricity parameter that determines their deviation from a perfect circle. The size and shape of each orbit are defined by its semi-major and semi-minor axes.

Understanding the Ellipse

• Definition of an ellipse
• Eccentricity and its significance
• Semi-major axis and semi-minor axis: size and shape

Unlocking the Secrets of the Ellipse: A Journey into Orbital Geometry

Embark on a captivating exploration of the ellipse, a mesmerizing curve that underpins countless phenomena in our universe. From celestial orbits to the shape of everyday objects, understanding the ellipse grants us a deeper appreciation for the intricate dance of nature.

Defining the Elusive Ellipse

An ellipse is a graceful curve that resembles a stretched circle, its two foci serving as the points from which it’s generated. Visualize a string tied to two fixed points and stretched with a pencil. As the pencil traces its path, it forms an oval-shaped shape, an ellipse.

Eccentricity: The Heartbeat of an Ellipse

Eccentricity, a crucial measure in the realm of ellipses, quantifies how much an ellipse deviates from a perfect circle. Ranging from 0 to 1, eccentricity determines the ellipse’s shape. A zero eccentricity yields a circle, while values closer to 1 produce increasingly elongated ellipses.

Size and Shape: Unveiling the Semi-Major and Semi-Minor Axes

Analogous to the limbs of a human body, the semi-major axis and semi-minor axis define an ellipse’s size and shape. The semi-major axis, the longest diameter, bisects the ellipse, while the semi-minor axis, the shorter diameter, intersects it perpendicularly.

Eccentricity: Circular or Eccentric Orbits

In the realm of celestial mechanics, the concept of eccentricity plays a pivotal role in defining the shape and path of an orbit. This enigmatic parameter holds the key to understanding the diversity of orbital trajectories, from perfectly circular celestial highways to highly elliptical cosmic roller coasters.

At its core, eccentricity is a measure of how much an orbit deviates from perfect circularity. Just as a circle has an eccentricity of zero, ellipses exhibit eccentricities ranging from zero to one. The greater the eccentricity, the flatter the ellipse becomes, resembling an elongated oval rather than a true circle.

Circular Orbits: A Celestial Symphony of Harmony

Circular orbits, with eccentricities hovering near zero, represent the epitome of celestial stability. Satellites and planets traversing these celestial highways maintain a constant distance from their central bodies, rotating around them like clockwork. The lack of ellipticity ensures that their paths never deviate significantly from a perfect circular symmetry.

Eccentric Orbits: A Cosmic Dance of Extremes

Contrastingly, eccentric orbits embrace a more dynamic and unpredictable nature. As their eccentricity increases, these orbits transform into elongated ellipses, with the orbiting bodies experiencing dramatic shifts in distance from their central objects. At the periapsis, the closest point to the central body, the orbiting object accelerates, while at the apoapsis, the farthest point, it slows down.

This eccentricity-induced dance results in a mesmerizing array of orbital paths. Highly eccentric orbits, with eccentricities approaching one, produce comet-like trajectories, where celestial bodies traverse vast distances before returning to their central objects. On the other hand, moderately eccentric orbits, such as those of Mars and Mercury, create unique challenges for spacecraft navigation, as they must account for the changing distances and velocities encountered along the elliptical path.

Eccentricity, with its ability to reshape orbits, serves as a fundamental parameter in celestial mechanics. From the circular elegance of planets to the eccentric dance of comets, this enigmatic parameter paints a vibrant tapestry of diversity in the cosmic arena.

Semi-major and Semi-minor Axis: Key Dimensions of an Ellipse

In the realm of astronomy and celestial mechanics, the ellipse stands as a fundamental geometric shape that describes the paths of heavenly bodies orbiting a central object. Within this elliptical canvas, the semi-major axis and semi-minor axis emerge as crucial dimensions that define the size and shape of the orbit.

Definitions and Importance

The semi-major axis, often denoted by “a”, represents the average distance between the orbiting object and its central focus. This distance serves as a measure of the overall size of the orbit. The semi-minor axis, labeled as “b”, on the other hand, denotes the shortest distance from the center of the ellipse to its edge. It determines the orbit’s width or narrowness.

Understanding these dimensions is vital for comprehending the dynamics of celestial orbits. They provide insights into the speed at which objects traverse their paths, the energy they possess, and the gravitational forces at play.

Relationship to the Size and Shape of an Ellipse

The semi-major axis dictates the length of the ellipse’s major axis, which connects the two farthest points from the center. The semi-minor axis, in contrast, determines the length of the minor axis, which is perpendicular to the major axis.

The ratio between the semi-major axis and semi-minor axis, known as the eccentricity, profoundly influences the shape of the ellipse. Eccentricity values ranging from 0 to 1 indicate varying degrees of ellipticity. A circular orbit exhibits an eccentricity of 0, implying equal values for both semi-major and semi-minor axes. As the eccentricity approaches 1, the orbit becomes increasingly elongated, resembling a thin, cigar-shaped trajectory.

The semi-major axis and semi-minor axis are indispensable parameters in uncovering the secrets of celestial orbits. They unveil the size, shape, and dynamics of these celestial paths, enabling scientists to unravel the mysteries of the cosmos. Understanding these dimensions empowers us to appreciate the intricate choreography of the universe and marvel at the beauty of celestial mechanics.

Inclination: The Tilt of Orbits

• Definition and impact on the orbital plane orientation
• Tilt of the path relative to a reference plane

Inclination: The Tilt of Orbits

Understanding the tilt of orbits, known as inclination, is crucial for comprehending the three-dimensional orientations of celestial bodies. Inclination measures the angle between an orbit’s plane and a reference plane. This reference plane can vary depending on the system being studied. In the solar system, we often use the plane of the Earth’s orbit around the Sun as the reference.

The tilt of an orbit affects how the object appears to an observer on the reference plane. An object with low inclination will appear to travel close to the reference plane, while an object with high inclination will appear to travel at a steeper angle.

Inclination is an important factor in determining the visibility and accessibility of celestial bodies. For example, satellites in orbit around Earth with high inclination can be difficult to track from ground-based observatories. Similarly, planets with high inclination orbits may only be visible from Earth during certain times of the year.

In addition to its impact on visibility, inclination can also influence an object’s interactions with other objects in its system. For example, objects with high inclination orbits may be more likely to collide with other objects that share their orbit. Inclination can also affect the amount of sunlight an object receives, which can influence its surface temperature and atmosphere.

By understanding the concept of inclination, astronomers can better understand the orientations and behaviors of celestial bodies, and how these factors can impact our observations and interactions with them.

Argument of Periapsis: Pinpointing the Closest Approach

In the celestial tapestry, celestial bodies dance in intricate orbits, each governed by a specific set of parameters. The argument of periapsis is one such parameter, offering a precise way to locate the closest point an orbiting object comes to a central object.

The argument of periapsis, often denoted by the Greek letter omega (ω), measures the angle between the ascending node (the point where an orbit crosses a reference plane) and the direction to the periapsis, the point of closest approach. It provides a precise coordinate system to map the orbit’s path.

To understand the argument of periapsis, consider a planet orbiting the sun. The ascending node marks the point where the planet’s orbit intersects the plane of the solar system. The line connecting the periapsis to the center of the sun is known as the periapse vector. The angle between the ascending node and the periapse vector represents the argument of periapsis.

The value of the argument of periapsis can range from 0 to 2π radians. When omega is equal to 0, the periapse is aligned with the ascending node. As omega increases, the periapse rotates in the orbital plane, until it reaches 2π radians, aligning with the ascending node again.

The argument of periapsis is closely related to the inclination and longitude of ascending node. These parameters together provide a comprehensive description of an orbit’s orientation in space. By combining the argument of periapsis with the other orbital elements, astronomers can precisely track the movements of celestial bodies and predict their future trajectories.

Longitude of Ascending Node: Mapping the Orbit

In celestial navigation, understanding the longitude of ascending node is crucial for mapping the orbit of an object, be it a planet, a satellite, or an asteroid. This angle plays a pivotal role in determining the orientation of an orbit in space and complements other orbital elements like inclination and argument of periapsis.

The longitude of ascending node, denoted by Ω, represents the angle between the ascending node and the vernal equinox. The ascending node is the point where an object’s orbit crosses the reference plane, typically the ecliptic plane in the solar system. The vernal equinox, on the other hand, is the point on the celestial sphere where the Sun crosses the celestial equator moving northward, marking the beginning of spring.

The longitude of ascending node provides a reference point that allows astronomers to determine the direction in which an object’s orbit is tilted. It helps them visualize the plane of the orbit and predict the object’s path through space. By combining the longitude of ascending node with inclination and argument of periapsis, scientists can fully characterize an object’s orbit, including its size, shape, and orientation.

Understanding the longitude of ascending node is essential for accurate spacecraft navigation and predicting celestial events. It enables scientists to track the movement of celestial bodies, plan space missions, and study the dynamics of our solar system and beyond.

Mean Anomaly: Mapping the Orbital Journey

Imagine an elliptical orbit, like a celestial dance where an object gracefully sweeps around a central body. The mean anomaly serves as a compass, guiding us through this cosmic choreography. It measures an object’s progress along its orbital path, providing a snapshot of its current position.

Calculating the mean anomaly involves a mathematical formula that considers the eccentric anomaly, a related concept that defines the object’s position in its orbit. By harnessing these calculations, astronomers can pinpoint an object’s location at any given time, allowing them to track its celestial journey.

The mean anomaly is particularly crucial in understanding the dynamic Keplerian elements, a set of parameters that fully describe an orbit. These elements include the eccentricity (shape), inclination (tilt), and semi-major axis (average distance). Together, they provide a comprehensive picture of an object’s orbital characteristics.

So, as celestial objects waltz through the cosmic expanse, the mean anomaly serves as a reliable guide, mapping their orbital progress and adding to our understanding of the celestial ballet that unfolds above our heads.