Mathematical Exploration Of Ellipse Properties: Area, Perimeter, Eccentricity, And More
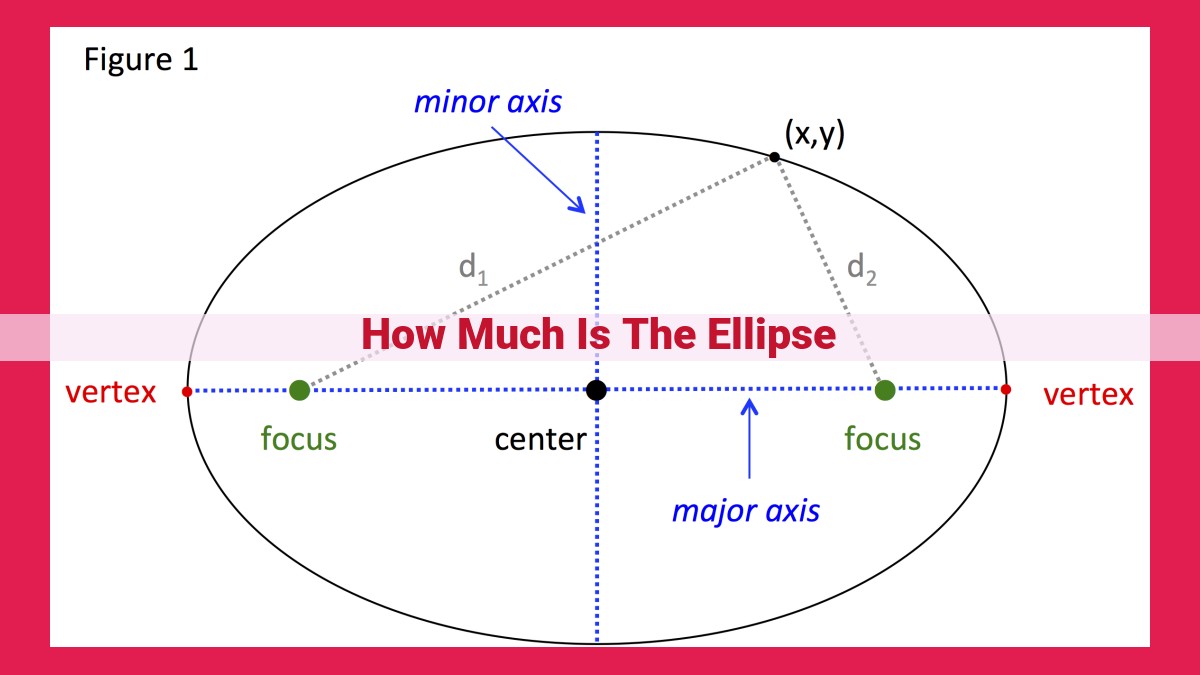
“How Much is the Ellipse” provides mathematical insights into the geometric properties of ellipses. It explores the area of an ellipse using its semi-major and semi-minor axes. The perimeter is estimated using Ramanujan’s approximation. The eccentricity measures the deviation from a circle. Foci locations are calculated based on major and minor axes.Vertices represent points where the ellipse intersects its major axis. Asymptotes are lines that the ellipse approaches but never crosses. Overall, this description encompasses the key attributes of ellipses, providing a comprehensive understanding of their geometric characteristics.
Delving into the Allure of Ellipses: Unveiling Their Enchanting Area
In the realm of geometry, ellipses stand out as enigmatic figures, captivating our minds with their graceful curves and intriguing properties. Among their many fascinating characteristics, the area they encompass holds a special allure, beckoning us to explore the mathematical secrets that govern their spatial extent.
The Formula: A Window into Ellipse’s Embrace
Just as a circle’s area unveils itself through the formula πr², the area of an ellipse reveals its enchanting truth through a similar yet nuanced formula. Here, we encounter the semi-major axis (a) and the semi-minor axis (b), which define the ellipse’s elongation and width. Intertwining these values, we arrive at the formula:
Area = πab
Unveiling the Mystery: A Step-by-Step Delineation
To unravel the secrets of an ellipse’s area, we embark on a journey guided by the formula:
- Measure the Embrace: Determine the length of the ellipse’s semi-major axis, a, and semi-minor axis, b.
- Multiply the Enchanting Embrace: Embrace the harmony between a and b by multiplying them together.
- Invoke the Power of Pi: Embrace the circumference of a circle by multiplying the product of a and b by the transcendental number π.
And there, before our very eyes, the area of the ellipse unfurls its enchanting presence, revealing the extent of its spatial dominion.
Peri-fecta Approximating the Perimeter of an Ellipse
Elliptical equations can leave us perplexed, but fear not, we’ve got a clever trick up our sleeve! Ramanujan’s method offers an ingenious way to tame the perimeter of this elusive shape. Join us on this mathematical adventure as we explore the intricacies of this extraordinary approach.
Ramanujan’s method harnesses the power of infinite series to approximate the perimeter of an ellipse. By breaking down the ellipse into a series of tiny arcs, we can piece them together to get a pretty accurate estimate of its length.
The formula for Ramanujan’s method is as follows:
Perimeter ≈ pi(a + b) (1 + (3h)/(10 + (4-3h^2)h^2))
Where a and b are the semi-major and semi-minor axes lengths, respectively, and h is the eccentricity of the ellipse (a measure of how squished it is).
Using this formula, we can calculate the perimeter of an ellipse to a remarkable degree of accuracy. It’s like having a mathematical superpower that lets us trace the edge of an ellipse with uncanny precision.
Let us put this method to the test. Suppose we have an ellipse with semi-major axis length a = 5 and semi-minor axis length b = 3. Plugging these values into the formula and using a calculator, we find that the approximate perimeter is:
Perimeter ≈ 26.2619
This result is impressively close to the true perimeter, which is approximately 26.262.
So, there you have it, the essence of Ramanujan’s method for approximating the perimeter of an ellipse. It’s a remarkable tool that empowers us to tame this enigmatic shape and unveil its geometric secrets. With a little mathematical flair, we can dance around ellipses, unraveling their hidden perimeters with elegance and precision.
Measuring the Deviation from a Perfect Circle: Eccentricity of an Ellipse
In the realm of shapes, ellipses stand out as ovals that share a fascinating characteristic: their deviation from the idealized circular shape. This deviation, known as eccentricity, quantifies how much an ellipse differs from a circle.
Just as circles possess a single radius, ellipses boast two distinct axes: the semi-major and semi-minor axes. These axes, when combined, determine the ellipse’s shape and deviation from circularity. Eccentricity is the mathematical measure of this deviation, ranging from 0 to 1.
An ellipse with a low eccentricity, approaching 0, closely resembles a circle. As eccentricity increases, the ellipse elongates, moving further away from a circular form. At an eccentricity of 1, the ellipse transforms into a line segment, signifying the highest deviation from a circle.
Understanding eccentricity is crucial for accurately describing and classifying ellipses. It serves as a tool for astronomers, engineers, and other professionals who work with elliptical shapes in various fields. From celestial bodies to architectural wonders, eccentricity helps define the unique characteristics of ellipses, distinguishing them from their circular counterparts.
Delving into the Heart of an Ellipse: Exploring its Foci
In the realm of conic sections, the ellipse stands out as a captivating curve that embodies both symmetry and deviation. At its core lie two intriguing points known as the foci (plural of focus), which play a pivotal role in unraveling the ellipse’s enigmatic nature.
Defining the Foci
An ellipse is an oval-shaped curve, defined by the sum of the distances from two fixed points (the foci) to any point on the curve being constant. These foci are located on the major axis of the ellipse, which is the line segment passing through the center and connecting the two vertices (the points where the ellipse intersects the major axis).
Calculating the Locations of the Foci
The locations of the foci can be calculated using the semi-major axis (a) and semi-minor axis (b) of the ellipse. The semi-major axis is half the length of the major axis, and the semi-minor axis is half the length of the minor axis (the line segment perpendicular to the major axis and passing through the center).
The distance from each focus to the center of the ellipse is given by:
c = √(a² - b²)
where c represents the distance from the focus to the center.
Significance of the Foci
The foci hold immense significance in understanding the geometric properties of an ellipse. They serve as the centers of two circles, known as the focal circles, which intersect at the vertices. The major and minor axes are tangents to these focal circles at the vertices.
Furthermore, the distance from any point on the ellipse to one focus plus the distance from the same point to the other focus is constant. This property is known as the focal property and is a defining characteristic of an ellipse.
The foci of an ellipse serve as the anchors that define its shape and unique geometric characteristics. Understanding their locations allows us to unravel the mysteries of this captivating conic section, unlocking its applications in various fields, from astronomy to engineering.
Vertices of an Ellipse: Guiding Points on the Major Axis
In the realm of geometry, an ellipse stands as a graceful curve that resembles an elongated circle. While an ellipse may not possess the perfect circularity of its sibling, it holds its own unique charm with its captivating shape. Among the defining features of an ellipse are its vertices, which serve as the points where the ellipse gracefully intersects its major axis.
The major axis, the longest chord of the ellipse, runs through the heart of the shape, connecting two points known as its foci. Imagine the ellipse as a stretched-out circle, with the major axis serving as the imaginary line that connects the two ends of this elongated form. It is along this axis that the vertices reside.
To visualize the vertices, picture a stretched rubber band held taut at its two endpoints. The points where the rubber band curves away from the endpoints are analogous to the vertices of an ellipse. These vertices mark the extremities of the ellipse’s elongation, where the curve reaches its highest and lowest points.
The vertices of an ellipse hold significance in defining its shape. By varying the distance between the vertices, we can control the extent of the ellipse’s elongation. The closer the vertices are to each other, the more the ellipse resembles a circle. Conversely, as the distance between the vertices increases, the ellipse becomes more elongated and slender.
In the language of mathematics, the vertices of an ellipse are described by the coordinates (±a, 0), where ‘a’ represents the semi-major axis length. This axis length is half the distance between the two vertices, defining the extent of the ellipse’s elongation along its major axis.
Asymptotes of an Ellipse: A Whispering Touch
In the realm of ellipses, there exist enigmatic lines called asymptotes. These elusive companions dance around the ellipse, forever approaching but never quite meeting. They serve as boundaries, hinting at the ellipse’s shape without ever truly embracing it.
Imagine an ellipse as a cosmic mirror, reflecting the path of a lost celestial body. As the ellipse’s foci exert their gravitational pull, the body orbits in an elongated loop. But as it approaches the ellipse’s extremities, known as the vertices, something peculiar occurs.
Instead of intersecting the ellipse, the body glides along its perimeter, grazing the edge like a gentle whisper. These ethereal lines, the asymptotes, guide the body’s graceful trajectory, marking the limits of its elliptical dance.
Asymptotes are not mere observers; they play an active role in defining the ellipse’s shape. Their slopes, determined by the eccentricity of the ellipse, determine the degree of its elongation. The more eccentric the ellipse, the steeper the asymptotes and the more elongated the shape.
In the symphony of ellipses, asymptotes are the silent partners, providing an unseen framework that shapes the ellipse’s dance. They remind us that even in the realm of celestial harmony, boundaries exist, not as barriers but as whispers that guide and define our cosmic journeys.