Comprehensive Guide: Domain Of Exponential Functions In Real Numbers
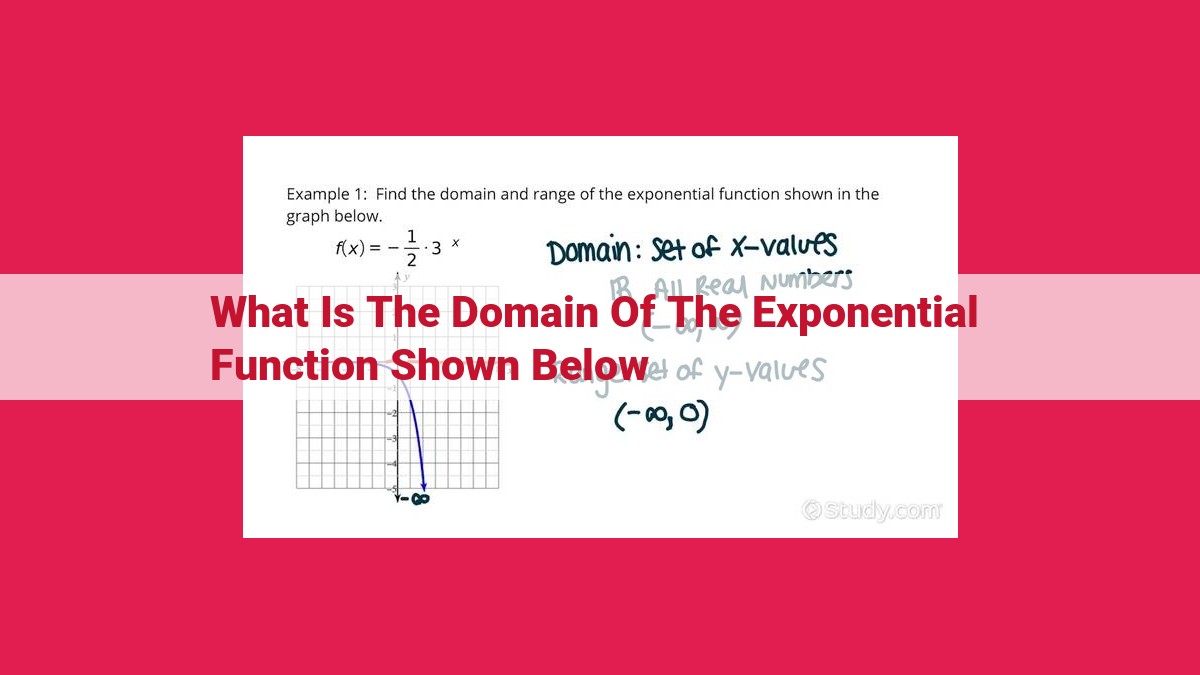
The domain of an exponential function is the set of all real numbers (except for special cases when the base is negative). This is because the exponent ‘x’ can take any real value, and the exponential function y = a^x is defined for all real values of x. Negative bases, however, restrict the domain to non-negative exponents, as raising a negative number to a negative power results in an undefined expression.
Unveiling the Mystique: A Journey into Exponential Functions
Step into the enchanting world of exponential functions, where numbers soar to unimaginable heights or dwindle to infinitesimal depths. Defined by the enigmatic symbol y = a^x, these functions empower us to unravel the secrets of growth, decay, and the intricate patterns that permeate our universe.
At the heart of exponential functions lie two key players: the base a and the exponent x. The base, a positive real number other than 1, dictates the rate at which the function grows or decays. A base greater than 1 results in exponential growth, while a base less than 1 leads to exponential decay.
The exponent, on the other hand, determines the magnitude of this growth or decay. A positive exponent signifies a multiplication of the base, multiplying the base by itself x times. Conversely, a negative exponent indicates division, dividing the base by itself x times.
Example: Consider the exponential function y = 2^x. With a base of 2, this function models exponential growth. As x increases, the value of y doubles with each step.
By understanding the interplay between base and exponent, we unlock the power of exponential functions to describe phenomena in various fields, from finance and population growth to scientific modeling and technological advancements.
Domain of Exponential Functions
Unveiling the Realm of Exponential Domains
Exponential functions, captivating mathematical entities, are defined as functions of the form y = a^x, where a represents the base and x denotes the exponent. The domain, the set of permissible values for the input x, plays a crucial role in understanding the behavior of exponential functions.
Real Numbers Reign Supreme
Generally, the domain of an exponential function encompasses all real numbers. This means that we can plug in any real number as the exponent x, regardless of whether it’s positive, negative, or even zero. This boundless domain allows exponential functions to model a wide range of phenomena, from exponential growth in biology to radioactive decay in physics.
Negative Bases: A Boundary in Disguise
However, the domain of exponential functions with negative bases presents a subtle twist. Consider the function y = (-2)^x. For negative bases, the domain becomes restricted to non-negative exponents only. This restriction stems from the definition of negative exponents, which involves taking reciprocals of positive exponents. For example, if x is negative in y = (-2)^x, the function would attempt to calculate the reciprocal of a negative number, which is undefined.
Intuitive Explanation: Avoiding Paradox
The restriction on negative exponents arises from the paradoxical nature of negative bases. If we allow negative exponents for negative bases, we would encounter situations like:
(-2)^-3 = 1 / (-2)^3 = 1 / -8 = -1/8
However, this result contradicts the fact that (-2)^-3 should be a positive number, according to the rules of exponents. To avoid such paradoxes, we limit the domain of exponential functions with negative bases to non-negative exponents.
Understanding the domain of exponential functions is essential for analyzing their behavior and applying them to real-world problems. The unrestricted domain of exponential functions with positive bases enables them to model a vast array of phenomena, while the restricted domain of exponential functions with negative bases safeguards against logical contradictions.
The Boundless Reach of Exponential Functions: Unraveling the Range
In the realm of mathematics, we encounter a class of functions that possess a remarkable characteristic: their ability to soar through all the real numbers. These are the exponential functions, defined by the equation y = a^x. Let’s delve into the magical range of exponential functions, exploring its implications for the shape of their graphs.
The Ubiquitous Range
The range of an exponential function is as expansive as the real number line itself, stretching from negative infinity to positive infinity. This means that no matter what value you input, the output will always be a real number. Consequently, the graph of an exponential function resembles a smooth curve that never intersects the x-axis.
Implications for the Graph
The unbounded range of exponential functions has profound implications for the shape of their graphs. First and foremost, they exhibit a characteristic upward or downward curvature, depending on whether the base ‘a’ is greater or less than one, respectively.
For example, when ‘a’ is greater than one (e.g., y = 2^x), the function grows exponentially as ‘x’ increases, creating a graph that curves upward. Conversely, when ‘a’ is less than one (e.g., y = (1/2)^x), it decays exponentially, resulting in a downward-curving graph.
Exponential Growth vs. Decay
The expansive range of exponential functions highlights their ability to model both exponential growth and exponential decay. In situations where a quantity increases rapidly over time, an exponential growth function provides an apt mathematical description. For instance, population growth or the spread of disease can be represented by exponential functions.
Conversely, when a quantity diminishes rapidly over time, an exponential decay function accurately captures the phenomenon. For example, radioactive decay or the cooling of a hot object can be modeled using exponential decay functions.
The range of an exponential function is a testament to its versatility. Stretching from negative to positive infinity, it enables exponential functions to represent a wide range of phenomena, from boundless growth to relentless decay. Whether describing the growth of bacteria or the cooling of a cup of coffee, exponential functions provide a powerful tool for capturing the dynamics of our ever-changing world.
Understanding Exponential Functions: Domain, Range, Codomain, and Input
Defining Codomain and Its Connection to Range
In mathematics, the codomain of a function refers to the set of all possible values that the function can output. It encompasses the range, which is the set of actual values that the function takes on. For exponential functions, the codomain is all real numbers, indicating that they can output any numerical value. This wide range is attributed to the inherent nature of exponential growth or decay, where the function can produce arbitrarily large or small values.
Significance of Input in Exponential Functions
The input of an exponential function is the exponent, x, which determines the output value y. A positive exponent corresponds to an increase in the base a, resulting in a larger output. Conversely, a negative exponent indicates a decrease, producing a smaller output. The exponent effectively controls the rate and direction of the exponential growth or decay.
For example, consider the exponential function y = 2^x. When x is positive, the output y increases rapidly as the base 2 is multiplied by itself repeatedly. However, when x is negative, the output decreases rapidly, approaching zero as the base 2 is divided by itself. This reflects the fundamental characteristic of exponential functions, where the input exponent has a profound impact on the output value.
Exploring Exponential Functions: From Basics to Applications
In the realm of mathematics, exponential functions stand as powerful tools for representing growth, decay, and other exponential phenomena. Let’s embark on a journey to unravel their essence, unveil their characteristics, and delve into their applications.
Unlocking the Definition: y = a^x
At the heart of every exponential function lies the fundamental equation y = a^x. Here, a represents the base, and x symbolizes the exponent. The base plays a pivotal role in determining the overall behavior of the function, while the exponent governs the rate of change.
Mapping the Domain: Real Numbers (Mostly)
The domain of an exponential function generally encompasses all real numbers. However, there’s a subtle exception when the base a is negative. In such cases, the domain is restricted to non-negative exponents to avoid imaginary numbers. This constraint stems from the nature of negative bases and the rules of exponentiation.
Exploring the Range: Unbounded Horizons
The range of an exponential function, on the other hand, embarks on a journey without bounds. It spans all real numbers, indicating that the function can assume any positive or negative value. This vast range has profound implications for the shape of the graph, giving rise to curves that soar high or plunge low, etching themselves onto the mathematical landscape.
Unraveling Related Concepts: Codomain and Input
The codomain of a function represents the set of possible output values, which, in the case of exponential functions, is identical to the range (all real numbers). The input, also known as the independent variable, drives the function’s behavior and determines the corresponding output through the power of exponentiation.
An Illustrious Example: y = 2^x
To solidify our understanding, let’s consider the exponential function y = 2^x. Its domain encompasses all real numbers, reflecting the boundless nature of its input. The range, mirroring the general rule, extends to all real numbers, opening up a vast realm of possible outputs. The codomain remains steadfast, embracing all real numbers as the function’s potential output space.
Navigating the graph of y = 2^x, we witness a steady ascent as the exponent grows. Every positive increment in x doubles the resulting value of y. On the other hand, negative exponents shrink y towards zero, highlighting the exponential decay inherent in the function.