Understanding Dne (Does Not Exist): Unprovable Mathematical Statements

DNE (Does Not Exist) is a mathematical term used to describe statements that cannot be proven true or false. Unlike the value “undefined” which refers to values outside the domain of a function, DNE applies to unprovable mathematical propositions. It is distinct from “false” statements as it does not imply the existence of an alternative true statement. DNE is often encountered in situations involving logical paradoxes, contradictions, and fallacies, highlighting the limitations of mathematical logic and the importance of careful reasoning.

Understanding the Enigmatic World of DNE in Mathematics

In the realm of mathematics, precision and clarity reign supreme. However, beneath the surface of familiar numbers and equations lies a curious realm where values and statements defy the confines of convention. Exploring these enigmatic concepts is not merely an exercise in abstract thought but a journey into understanding the nuances and complexities of mathematics.

Undefined: When Values Escape the Realm of Meaning

Just as a ship can sail beyond the horizon, certain mathematical values can venture into uncharted territory. These are the Undefined values, which reside outside the domain of the function in question. Like a door to an unknown dimension, undefined values represent the absence of a meaningful result for a given input.

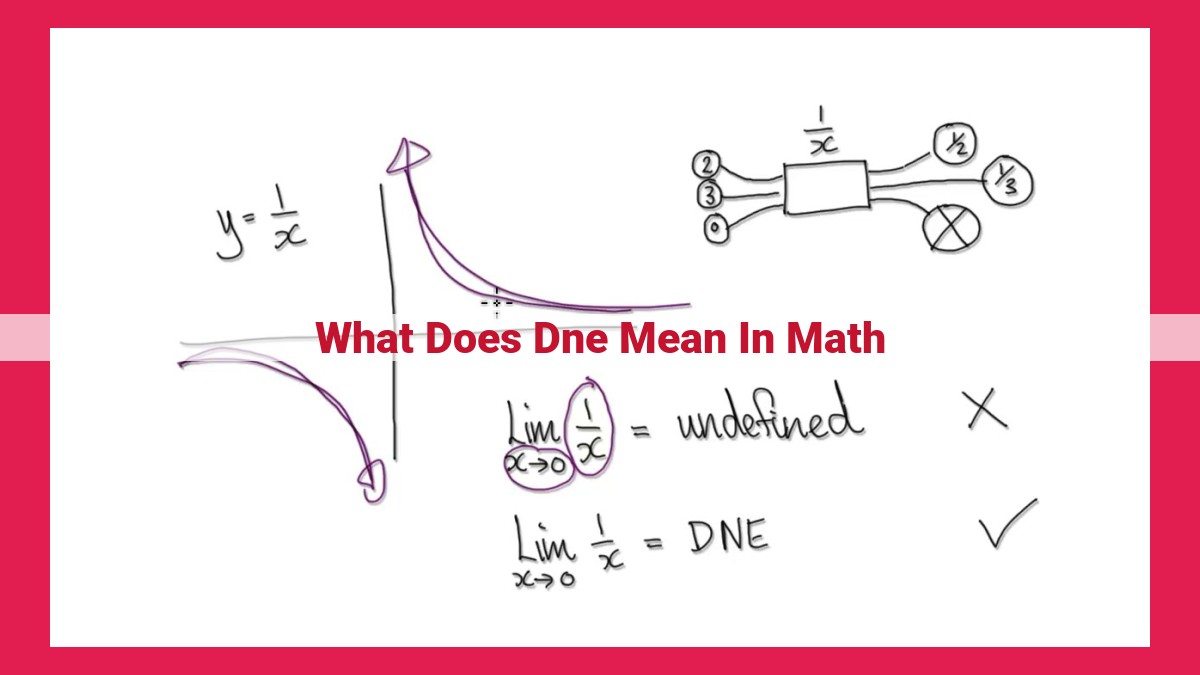
Consider the query, “What is 1 divided by 0?” In the world of arithmetic, this equation does not exist. There is no finite number that, when multiplied by 0, yields 1. Hence, division by zero remains undefined, a tantalizing mystery that defies logical explanation.

Does Not Exist (DNE): Unraveling the Secrets of Paradox

Beyond undefined values, mathematics unfolds a realm of unprovable statements, denoted by the enigmatic acronym DNE. Unlike “false” statements, which can be proven incorrect, DNE statements defy the boundaries of truth and falsehood. They inhabit a realm where logic falters and paradoxes dance.

The famous “Liar’s Paradox” epitomizes this enigmatic world. It asserts that “This statement is false.” If the statement is true, then it must be false. Conversely, if the statement is false, then it must be true. Caught in this logical vortex, we find ourselves in the realm of DNE, where the very fabric of logic trembles.

Values Outside the Domain: Exploring Undefined

In the realm of mathematics, we encounter values that defy our expectations and push the boundaries of logic. These values lie outside the domain of defined functions, rendering them undefined. Understanding these enigmatic quantities is crucial for expanding our mathematical comprehension.

Defining Undefined

Undefined is a mathematical term used to describe something that cannot be calculated or assigned a specific value within a given context. This occurs when a function is evaluated at a point where it is not defined, resulting in an expression that cannot be solved. For instance, the function f(x) = 1/x is undefined when x = 0, as division by zero is not a valid operation.

Related Concepts: Null, Missing, and NaN

Undefined should not be confused with other related concepts:

• Null represents the absence of a value, often used to indicate that data is not available or has not been assigned.
• Missing is similar to null, but it typically refers to a value that is expected to be present but is not found.
• Not a Number (NaN) is a special value used in floating-point arithmetic to represent invalid numerical expressions, such as calculations involving division by zero or taking the square root of a negative number.

Examples of Undefined Values

• The function f(x) = log(x) is undefined for x ≤ 0 because the logarithm of a negative number is not a real number.
• The function f(x) = x^2 – 4 is undefined for x = 2 and x = -2 because the expression becomes a division by zero at these points.
• The function f(x) = 1/(x-2) is undefined for x = 2 because it would result in the indeterminate form of 1/0.

Understanding the concept of undefined is paramount for interpreting mathematical expressions correctly and avoiding common pitfalls in calculations. It serves as a reminder that not all values are accessible within a given function, and that evaluating functions at undefined points can lead to erroneous results.

Does Not Exist (DNE): Unprovable Statements

In the realm of mathematics, we often encounter statements that cannot be proven or disproven, leaving us in a perplexing state of uncertainty. These enigmatic statements are known as “Does Not Exist (DNE).” Unlike false statements, which can be shown to be incorrect, DNE statements exist in a gray area, neither true nor false, forever dancing on the cusp of mathematical reason.

DNE statements often arise from paradoxes, those mind-bending puzzles that lead to contradictory conclusions. Consider the famous Russell’s paradox, which asks the question: Is the set of all sets that do not contain themselves a member of itself? If it is, then it should contain itself, violating its own definition. If it is not, then it should contain itself, again contradicting its own nature. Such paradoxes lead us to the paradoxical conclusion that the set of all such sets DNE.

Other concepts closely related to DNE are contradictions and fallacies. A contradiction occurs when two statements are both simultaneously true and false, which is mathematically impossible. Fallacies, on the other hand, are errors in reasoning that lead to false conclusions. Understanding DNE, contradictions, and fallacies is crucial for navigating the treacherous waters of mathematical reasoning, helping us to identify and avoid pitfalls in our logical arguments.

Ultimately, DNE statements remind us of the limitations of our mathematical systems. They serve as a testament to the vast expanse of the unknown, stretching beyond the boundaries of our current understanding. While they may not provide clear-cut answers, DNE statements challenge us to think critically, question our assumptions, and push the frontiers of mathematical knowledge.

Infinite: Exploring the Concept of Boundless Values

In the vast realm of mathematics, we encounter a concept that transcends our everyday understanding of numbers – infinity. It’s a notion that stretches beyond any finite limit, representing a realm of boundless values.

The symbol for infinity is an elegant figure-eight turned on its side, ∞. It’s a fitting representation for something that can extend in both directions, positive and negative. Positive infinity is denoted by ∞, while negative infinity is represented by -∞.

Infinity is closely intertwined with the concept of limits. When we study the behavior of a function as its input approaches a certain value, we may find that the output approaches infinity. For example, as the input of the function 1/x approaches 0, the output approaches positive infinity.

Convergence and series are other important concepts related to infinity. A series is an infinite sum of terms. When the sum of the terms converges to a finite value, the series is said to converge. However, if the sum keeps growing without bound, the series diverges to infinity.

Examples of infinite values can be found in nature and everyday life. The number of stars in the universe, the digits of pi, and the time it would take to count to infinity are all examples. These values stretch beyond our comprehension, but they serve as a reminder of the vastness of the mathematical landscape.

Understanding the concept of infinity is crucial for expanding our mathematical reasoning. It allows us to explore the limits of our knowledge and push the boundaries of logic. By embracing the notion of boundless values, we open ourselves up to a deeper understanding of the world around us.

Not a Number (NaN): The Enigma of Invalid Numerical Values

In the realm of mathematics, we encounter not just numbers, but also special values that challenge our perception of what constitutes a numerical value. One such enigmatic entity is NaN, an acronym for “Not a Number.” This peculiar concept plays a crucial role in floating-point arithmetic, extending the boundaries of mathematical representation.

Defining NaN: A Numerical Paradox

NaN is a unique value in the realm of numbers. It is neither positive nor negative, finite nor infinite, real nor imaginary. It signifies an undefinable result, a mathematical quandary that arises when an operation yields an invalid numerical outcome. For example, attempting to divide zero by zero in floating-point arithmetic results in NaN.

NaN vs. Infinity and Undefined

NaN is distinct from both infinity and undefined. Infinity represents boundless values, while undefined indicates that a value cannot be determined due to a lack of information. NaN, on the other hand, signifies an invalid operation, a paradoxical outcome that cannot be categorized as either infinity or undefined.

Properties and Applications of NaN

NaN possesses several unique properties that make it indispensable in floating-point arithmetic. First, NaN is contagious. When NaN is involved in an operation, the result is always NaN, regardless of the other operand. This ensures that invalid operations are propagated throughout calculations, preventing erroneous results from being propagated.

Second, NaN is propagated through mathematical functions. If even one operand is NaN, the result of any function applied to that operand will also be NaN. This property allows for robust error handling in mathematical calculations.

Finally, NaN is used in various applications, including:

• Representing missing values in datasets
• Indicating invalid inputs in numerical modeling
• Detecting errors in floating-point calculations

The concept of NaN enriches our understanding of mathematical values. It challenges the traditional notion of numbers and extends the boundaries of logic. By introducing the concept of an invalid numerical value, NaN enables us to handle exceptional cases in mathematical operations and expand the scope of our computations. As we delve deeper into the world of mathematics, embracing concepts like NaN allows us to push the limits of our understanding and explore the infinite possibilities that lie beyond the confines of traditional numerical representation.