Distinguishing Parallelograms: Understanding Trapezoids, Rectangles, And Rhombuses
Not all quadrilaterals are parallelograms. Quadrilaterals without two pairs of parallel sides, such as trapezoids, are not parallelograms. Additionally, rectangles (quadrilaterals with four right angles) and rhombuses (quadrilaterals with four congruent sides) are distinct from parallelograms because they meet additional criteria beyond having two pairs of parallel sides of equal length.
Understanding Parallelograms: A Geometrical Adventure
In the realm of geometry, there exists a fascinating shape known as the parallelogram, a quadrilateral that embodies a unique combination of properties. A parallelogram is defined as a quadrilateral with two pairs of parallel sides of equal length. Imagine a shape resembling a stretched-out rectangle, where the opposite sides are not only parallel but also of the same length.
To illustrate this concept further, let’s embark on a geometrical journey. Consider a quadrilateral with four sides labeled AB, BC, CD, and DA. If we were to measure the lengths of these sides, we would find that AB is equal to CD, and BC is equal to DA. Additionally, when we investigate the angles between these sides, we would notice that the opposite angles are congruent. This means that angle A is equal to angle C, and angle B is equal to angle D.
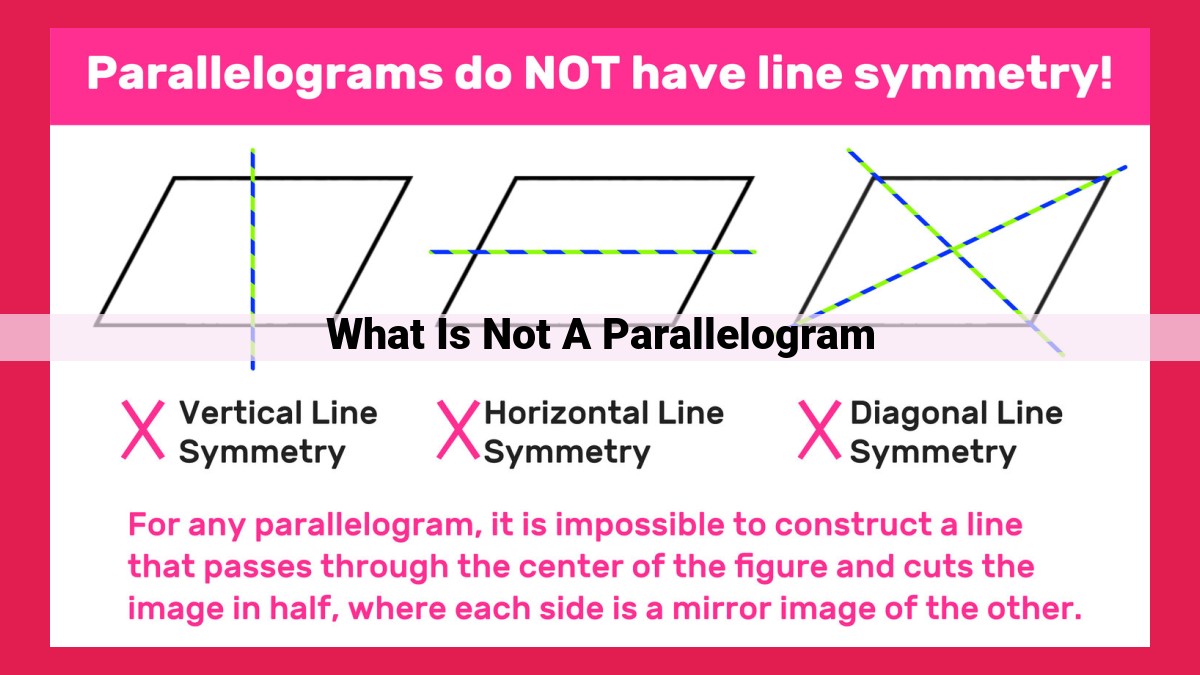
Now, let’s pause here and take a closer look at the parallel sides of a parallelogram. This defining characteristic sets it apart from other quadrilaterals. Parallel lines are lines that never intersect, regardless of how far they are extended. In the case of a parallelogram, the two pairs of parallel sides create a sense of symmetry and balance.
Quadrilaterals That Fall Short of Parallelogram Credentials
In the realm of geometry, quadrilaterals occupy a prominent place, with parallelograms standing out as distinctive figures. However, not all quadrilaterals share the illustrious status of parallelograms.
Quadrilaterals, as their name suggests, are four-sided polygons. Parallelograms, the quintessential quadrilaterals, are defined by their unique trait: two pairs of parallel sides of equal length. This harmonious arrangement distinguishes them from other quadrilaterals that lack this defining characteristic.
Take, for instance, trapezoids. These peculiar quadrilaterals boast only one pair of parallel sides. As a result, their parallel sides never coincide in length, disqualifying them from the esteemed rank of parallelograms.
Another quadrilateral that misses the parallelogram mark is the rectangle. This enigmatic shape exhibits four right angles, a feature that sets it apart from parallelograms. The absence of parallel sides further cements its non-parallelogram status.
Rhombuses also fall short of the parallelogram criteria. While they flaunt four congruent sides, their parallel sides are not of equal length. This subtle distinction relegates them to a different geometrical category.
In essence, quadrilaterals that lack two pairs of parallel sides of equal length cannot claim the title of parallelograms. These shapes, such as trapezoids, rectangles, and rhombuses, possess their own unique characteristics that set them apart from their parallelogram counterparts.
Quadrilaterals: Not All Created Equal
In the vast and fascinating world of geometry, we encounter a myriad of shapes. Among them are quadrilaterals, four-sided figures that can vary greatly in their properties. While parallelograms stand out as a unique and distinctive type of quadrilateral, there are several other types that do not meet the strict criteria of a parallelogram.
Trapezoids: One Pair Does Not Make a Parallelogram
Picture a quadrilateral with just one set of parallel sides. This is what we call a trapezoid. Unlike parallelograms, which boast two pairs of parallel sides, trapezoids have only one. This single pair of parallel sides runs parallel to each other, creating a shape that resembles a trapezoid, the shape of a trapezoidal prism.
Rectangles: Right Angles Rule
Imagine a quadrilateral with four right angles. This is the hallmark of a rectangle, a quadrilateral that defines both sides of a perfect square or rectangle. Its sides are perpendicular, meeting at right angles. Unlike parallelograms, rectangles do not have opposite sides that are parallel, which is a key characteristic of parallelograms.
Rhombuses: Equal Sides, but Not Parallel
Envision a quadrilateral with four congruent sides. This is a rhombus, a quadrilateral that shares the property of equal sides with parallelograms. However, the crucial difference lies in the absence of parallel sides in rhombuses. The sides of a rhombus are not parallel, which sets it apart from its parallelogram counterparts.
**Parallelograms and Their Non-Parallelogram Counterparts**
In the realm of geometry, parallelograms stand out as distinctive quadrilaterals, characterized by their unique combination of parallel sides. However, not all quadrilaterals enjoy this special designation. Let’s dive into the world of quadrilaterals and explore the key differences that set parallelograms apart from their non-parallelogram kin.
**Recognizing a Parallelogram**
At the heart of a parallelogram’s identity lies the presence of two pairs of parallel sides of equal length. This arrangement gives parallelograms their characteristic opposite sides that are congruent. Imagine a rectangular frame or a kite soaring through the sky – these everyday objects embody the essence of parallelograms.
**Quadrilaterals That Miss the Mark**
Not all quadrilaterals qualify as parallelograms. Let’s meet some of their non-parallelogram counterparts:
-
Trapezoids: These quadrilaterals have only one pair of parallel sides, leaving the other two sides unparallel.
-
Rectangles: Known for their four right angles, rectangles possess all sides of equal length, but they lack the defining characteristic of having two pairs of parallel sides.
-
Rhombuses: These quadrilaterals boast four congruent sides, but unlike parallelograms, their opposite sides are not parallel.
**Comparative Summary: Parallelograms vs. Non-Parallelograms**
To clearly distinguish parallelograms from their non-parallelogram counterparts, let’s compare their key characteristics:
| Feature | Parallelograms | Non-Parallelograms |
|---|---|---|
| Number of Pairs of Parallel Sides | Two | One or None |
| Length of Opposite Sides | Equal | Not necessarily equal |
| Right Angles | Not necessarily | All sides (rectangles) |
| Congruent Sides | Not required | All sides (rhombuses) |
**Applications and Examples**
Understanding the distinctions between parallelograms and other quadrilaterals holds practical significance in various fields:
- Architecture: Parallelograms form the basis of many architectural designs, providing structural stability and aesthetic appeal.
- Construction: Parallelograms are used in roof trusses and other structural elements to distribute weight evenly.
- Engineering: Parallelograms are employed in mechanical linkages, gears, and other mechanisms to transfer motion smoothly.
Key Distinguishing Features: Understanding Parallelograms vs. Non-Parallelograms
Laying the Groundwork
In the realm of quadrilaterals, parallelograms stand out with their unique set of characteristics that differentiate them from other four-sided figures. To fully grasp the essence of parallelograms, it’s crucial to comprehend the decisive differences that set them apart from their quadrilateral counterparts.
Parallelism and Equality: The Cornerstones of Parallelograms
The defining trait of parallelograms lies in their parallelism. They possess two pairs of parallel sides, indicating that these sides never intersect and always run parallel to each other. Moreover, these parallel sides are also congruent, meaning they are of equal length. This combination of parallelism and equal side lengths forms the cornerstone of parallelograms.
Distinguishing Parallelograms from Their Quadrilateral Cousins
Understanding these key features is essential for differentiating parallelograms from other quadrilaterals. For instance, trapezoids possess only one pair of parallel sides, while rectangles have four right angles but lack parallel sides of equal length. Rhombuses, on the other hand, boast four congruent sides but deviate from having two pairs of parallel sides.
Emphasizing the Essential Criteria
To recognize a parallelogram accurately, it’s imperative to remember that it must satisfy two distinct criteria:
- It must have two pairs of parallel sides.
- These parallel sides must also be congruent in length.
Meeting these two criteria guarantees that the figure in question is indeed a parallelogram.
Practical Applications and Real-World Significance
Comprehending the distinctions between parallelograms and other quadrilaterals holds practical significance in various fields. Engineers utilize this knowledge in designing structures, architects in crafting buildings, and artists in creating visually pleasing compositions. Understanding these geometrical concepts empowers individuals to navigate the world around them with greater precision and comprehension.
Applications and Examples: Distinguishing Parallelograms from Other Quadrilaterals
Beyond the theoretical realm, the distinction between parallelograms and other quadrilaterals holds practical significance in various applications. An astute understanding of these geometrical concepts empowers us to navigate the world around us effectively.
Consider architecture, where parallelograms play a crucial role in designing sturdy and aesthetically pleasing structures. Their inherent symmetry and load-bearing capabilities make them ideal for constructing bridges, roofs, and even entire buildings. The Golden Gate Bridge, for instance, is renowned for its iconic orange-hued parallelogram-shaped towers that support its massive suspension cables.
Engineering also relies heavily on the properties of parallelograms. Gear systems, composed of interconnected gears with teeth shaped like parallelograms, transmit motion efficiently and smoothly between rotating shafts. In automotive design, parallelograms form the foundation of suspension systems, ensuring optimal handling and a comfortable ride.
Textile manufacturing is another industry where parallelograms shine. The looms used in weaving fabrics utilize a series of interconnected parallelograms to interlace threads, creating intricate patterns and textures. Similarly, quilters often employ parallelograms as the building blocks of their vibrant creations, adding depth and visual interest to their work.
Nature itself provides countless examples of parallelograms. Crystals such as calcite often exhibit parallelogram-shaped faces due to their crystalline structure. In the animal kingdom, the parallelogram-shaped wings of butterflies and moths allow for graceful and efficient flight.
By understanding the distinct characteristics of parallelograms, we gain invaluable insights into the world around us. Whether in architecture, engineering, manufacturing, or even the natural environment, parallelograms play a vital role in shaping our experiences and improving our lives.