Discover The Slope Of Parallel Lines: A Comprehensive Guide

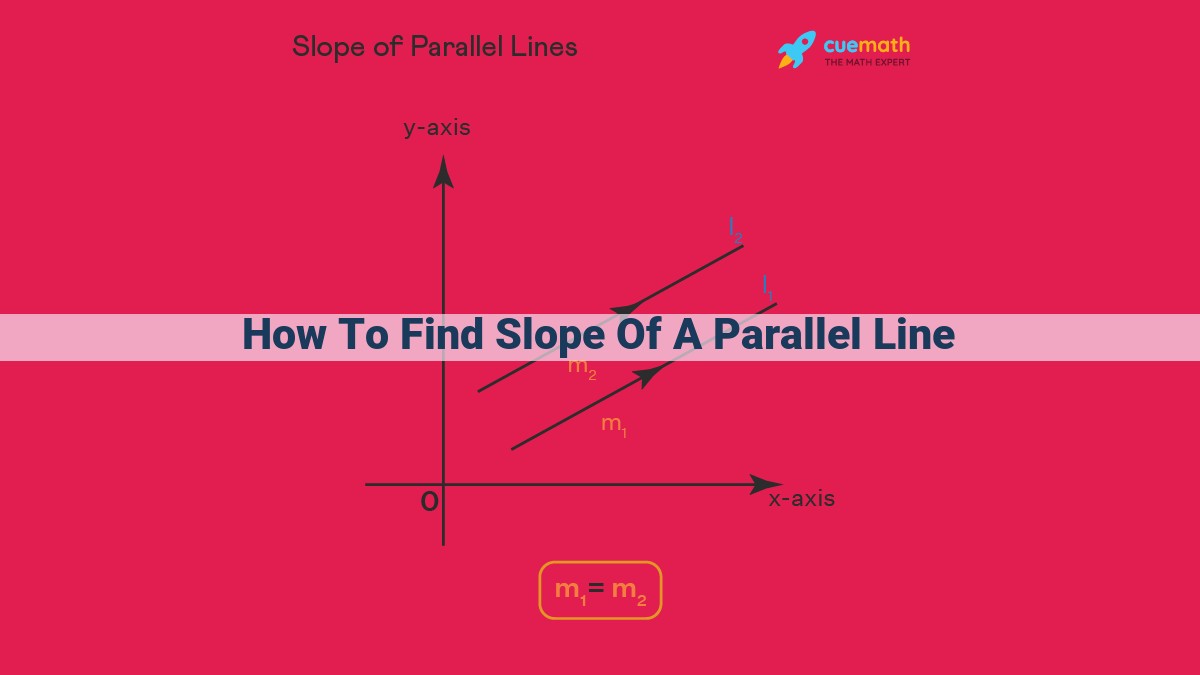
To find the slope of a parallel line:

• Identify a parallel line or the equation of the given line.
• Since parallel lines have equal slopes, use the slope of the given line or any parallel line.
• If given two distinct points on the parallel line, use the slope formula: slope = (y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2) are the points.

• Define parallel lines as lines that never intersect and have the same slope.
• Explain the significance of slope in understanding the orientation and relationship between lines.

Parallel Lines: A Tale of Slopes and Unending Paths

In the realm of geometry, where lines dance across the page, there exists a special bond between lines that never cross each other, like steadfast companions on parallel paths. These parallel lines share a common trait: their slopes are identical.

Slope: The Measure of Inclination

Imagine a hill rising from the ground. The slope of the hill, a measure of its steepness, is determined by the rise, the vertical change, and the run, the horizontal change. In the same way, the slope of a line is the ratio of its rise (change in y) to its run (change in x).

Calculating the Slope: A Formulaic Adventure

To calculate the slope of a line, we embark on a quest for distinct points. Armed with these coordinates, we unleash the slope formula: (y2 - y1) / (x2 - x1). This formula reveals the slope of the line connecting the points (x1, y1) and (x2, y2).

Parallel Lines: United by Slope

Now, let’s unravel the secret of parallel lines and their shared slope. Just as two knights on parallel paths maintain an unspoken agreement, parallel lines adhere to the principle of equal slopes. The slope of any line parallel to a given line will be the same as the slope of the given line, creating a harmonious coexistence.

Finding the Slope of Parallel Lines: A Step-by-Step Journey

To uncover the slope of a parallel line, we embark on a three-step adventure:

1. Identify the parallel line or the equation of the given line.
2. Unleash the power of the slope formula, wielding the slope of the given line or any other parallel line.

Slope: Understanding Rise and Run

• Introduce the concept of slope as the ratio of rise (change in y) to run (change in x).
• Describe the slope triangle as a visual representation of rise and run.

Slope: Understanding Rise and Run

In the realm of mathematics, lines play a pivotal role in shaping our understanding of geometry and spatial relationships. Among the fundamental properties of lines is slope, which provides valuable insights into the line’s orientation and behavior. Slope, simply put, is the measure of a line’s steepness or incline. It’s the ratio of the rise (change in the y-coordinate) to the run (change in the x-coordinate) of a line.

Visualize a line on a graph. Imagine you’re standing at the bottom of a slope, looking up towards its peak. The rise would be the vertical distance you ascend, while the run would be the horizontal distance you cover. By calculating the ratio of these two values, you obtain the slope of the line.

The Slope Triangle: A Pictorial Guide

Understanding the concept of slope is greatly aided by the slope triangle. This triangle, formed by any three points on a line, provides a visual representation of rise and run. The horizontal side of the triangle represents the run, and the vertical side represents the rise. The slope is then determined by the ratio of the length of the vertical side to the length of the horizontal side.

Importance of Accurate Points

It’s crucial to note that the accuracy of the points used in calculating the slope is paramount. The slightest error in point selection can lead to a misrepresentation of the line’s true slope. Therefore, it’s essential to choose points that are clearly defined and lie on the same line.

Real-World Applications

The concept of slope finds widespread application in various fields. In architecture, for instance, it’s used to determine the slope of roofs and ensure proper drainage. In construction, it’s crucial for calculating the incline of ramps and stairs to meet safety standards. Engineers rely on slope to assess the stability of structures and design efficient transportation systems.

Calculating Slope Using Points: Unlocking the Secrets of Parallel Lines

To determine the slope of a line, we need at least two distinct points lying on that line. The slope, a measure of the line’s steepness and orientation, is calculated using these points.

The slope formula is a mathematical equation that calculates the slope using the coordinates of two points, $(x_1, y_1)$ and $(x_2, y_2)$:

Slope = (y2 - y1) / (x2 - x1)

By calculating the slope, we uncover a valuable property of parallel lines: their shared slope. Parallel lines, by their very nature, never intersect and run alongside each other, maintaining the same slope throughout their length.

Steps for Finding the Slope of a Parallel Line:

1. Identify a parallel line or the equation of the given line: If you have a parallel line, you can directly use its slope. Otherwise, identify the equation of the given line and extract its slope.
2. Use the slope of the given line or any parallel line: Since parallel lines share the same slope, you can use the slope of any parallel line to find the slope of the desired line.

By understanding the concept of slope and how to calculate it using points, we gain valuable insights into the relationships between lines. Whether you’re an architect designing buildings, an engineer constructing bridges, or a student studying geometry, the ability to find the slope of parallel lines is a fundamental tool that unlocks a wealth of knowledge and applications.

Understanding the Secret Code: Slope and Parallel Lines

In the realm of geometry, lines dance across the page, forming an intricate tapestry of patterns. Among these lines, parallel lines stand out as special entities that share a hidden secret: they possess the same slope.

Slope, a term that may have sparked curiosity in your math classes, unravels the orientation and relationship between lines. It is a measure of how steeply a line ascends or descends, expressed as the ratio of rise (change in y-coordinates) to run (change in x-coordinates).

Now, here’s the fascinating part: parallel lines have equal slopes. This means that the angle at which they tilt is identical. Picture two train tracks running side by side; they never intersect and always maintain the same distance from each other. Similarly, parallel lines on a graph paper, like two lanes of a highway, remain equidistant and share the same slope.

The reason behind this shared slope is simple. Imagine a parallel line to a given line, say, a line segment connecting points A and B. If we measure the slope of this parallel line, we will find that it is the same as the slope of the line segment AB. Why? Because the rise and run of the parallel line are in proportion to those of the line segment AB.

Steps to Find the Slope of a Parallel Line:

1. Identify the Parallel Line: Determine the parallel line or the equation of the given line.

2. Use the Slope: The slope of the parallel line will be the same as the slope of the given line or any other parallel line.

This concept of parallel lines and shared slope finds applications in various fields, from architecture to engineering. By understanding this fundamental relationship, we can decipher the secrets hidden within the language of lines and unlock the power of geometry.

Finding the Slope of Parallel Lines: A Simple Guide

In the world of geometry, parallel lines hold a special relationship, never intersecting and maintaining the same orientation. Understanding their properties, particularly their slope, is essential for various applications.

The Slope Triangle: Rise and Run

Before exploring parallel lines, let’s revisit the concept of slope. Slope measures the steepness or inclination of a line, represented as the ratio of rise (change in y) to run (change in x). Visualize a slope triangle formed by two points on a line, with a hypotenuse parallel to the line.

Calculating Slope Using Points

To calculate the slope, we use the formula: slope = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of the two points. This formula essentially represents the rise over run.

Parallel Lines and Shared Slope

Now, back to our focus: parallel lines. The key principle here is that parallel lines have equal slopes. No matter how far apart they are, their slopes will always match. This shared slope property is fundamental to understanding parallel lines.

Steps for Finding the Slope of a Parallel Line

To find the slope of a parallel line, follow these simple steps:

1. Identify a parallel line or the equation of the given line. If you have a specific parallel line, simply use its slope.
2. Use the slope of the given line or any parallel line. If you have the equation of the given line, solve for the slope by rewriting it in slope-intercept form (y = mx + b), where m represents the slope.

Importance and Applications

Understanding the slope of parallel lines has practical applications in fields like construction, engineering, and architecture. By accurately determining slopes, professionals ensure the stability and precision of structures and designs.

Remember, the key to success is to accurately identify the points and understand the concept of parallel lines. With this knowledge, you’ll be well-equipped to tackle any problem involving parallel lines and their slopes.

Importance and Applications

• Emphasize the importance of using accurate points and understanding the concept of parallel lines.
• Provide examples or real-world applications where finding the slope of parallel lines is crucial, such as in architecture, construction, or engineering.

Understanding Slope: A Key to Parallel Lines

In the realm of geometry, parallel lines play a pivotal role, always coexisting without ever colliding. The essence of their distinct nature lies in their slope, a numerical measure that depicts the line’s orientation and relationship with other lines.

Slope: Rise and Run

Slope is essentially the ratio of vertical change (rise) to horizontal change (run) along a line. Visualize a slope triangle, where the opposite side represents the rise, and the adjacent side represents the run. This triangle offers a tangible representation of the line’s ascent or descent.

Calculating Slope Using Points

To quantify slope, we delve into the slope formula:

slope = (change in y) / (change in x)

where (change in y) is the rise and (change in x) is the run between two distinct points (x1, y1) and (x2, y2) on the line.

Parallel Lines: Shared Slope

The intriguing connection between parallel lines comes into play in the world of slopes. Lines that never intersect, always maintaining their parallel stance, boast a captivating secret: equal slopes. No matter where you venture along these parallel paths, their slopes remain invariant, reflecting their unwavering adherence to their distinct orientations.

Finding the Slope of a Parallel Line

Seeking the slope of a parallel line is a straightforward endeavor:

1. Locate a parallel line: This could be an existing line or one derived from the equation of the given line.

2. Adopt the slope: Embrace the slope of the identified parallel line, as it inherently matches the slope of all its parallel counterparts.

Importance and Applications

Beyond theory, the concept of parallel lines and their slopes finds crucial applications in real-world scenarios:

• Architecture: Ensuring parallel walls and aligning supporting beams relies heavily on accurate slope calculations.

• Construction: From sloping roofs to leveling foundations, understanding slope is paramount in every aspect of building.

• Engineering: Designing bridges, tunnels, and towering structures demands precise slope determination to maintain stability and functionality.

Parallel lines, characterized by their non-intersecting nature and shared slope, serve as fundamental building blocks in geometry. Their mathematical underpinnings provide a solid framework for addressing real-world challenges and unlocking the secrets of our built environment. From skyscrapers to bridges, the slope of parallel lines quietly whispers its importance in every architectural and engineering marvel.