Discover The Period Of Y = Csc(X) And Its Impact On Graph Characteristics

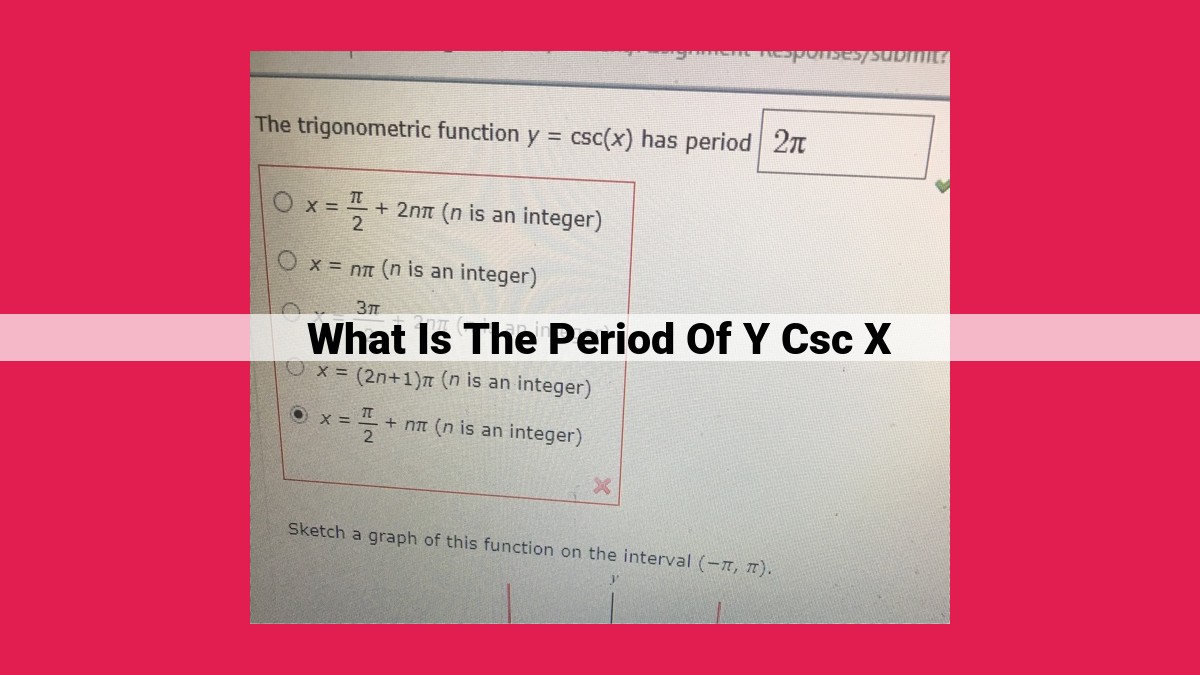
The period of y = csc(x) is 2π, which means that the graph repeats itself every 2π units on the x-axis. This is because the sine function, which is the denominator of csc(x), has a period of 2π. As a result, the reciprocal of the sine function also has a period of 2π. The period can be visualized on the graph of y = csc(x) as the distance between successive vertical asymptotes, which occur at x = nπ/2, where n is an integer.

Explain the concept of period for functions, including the period of y = csc(x) as 2π.

The Elusive Period of the Cosecant Function: A Mathematical Journey

In the realm of trigonometry, the cosecant function stands out as an enigmatic entity. Its elusive period, unlike that of its trigonometric companions, holds a captivating mystery. Let’s embark on a mathematical expedition to unravel this enigma and explore the intricacies of y = csc(x).

Defining the Period: A Cyclic Pattern

Just as the seasons cycle through predictable intervals, mathematical functions also exhibit periodic behavior, repeating their values over regular intervals. The period of a function represents the distance along the input axis that must be traversed for the function to complete one full oscillation.

For the cosecant function, this magical interval is 2π. This means that as you move 2π units along the x-axis, the graph of y = csc(x) repeats itself. This is in stark contrast to the sine and cosine functions, which have periods of 2π and 2π, respectively.

Beyond the Period: Related Concepts

Our journey into the world of y = csc(x) leads us to an array of related concepts that further illuminate its nature.

Periodic Functions: A Symphony of Repetition

Functions that display periodic behavior are aptly named periodic functions. Y = csc(x), with its period of 2π, proudly wears this label. Its values dance in a cyclical pattern, much like the hands of a clock.

Amplitude: An Elusive Attribute

In the realm of trigonometry, the amplitude represents the vertical distance between a function’s maximum and minimum values. However, for y = csc(x), this concept remains elusive. Unlike sine and cosine, it lacks well-defined maximums and minimums, rendering its amplitude undefined.

The Sine Connection: A Reciprocal Embrace

Y = csc(x) harbors a special relationship with its trigonometric sibling, y = sin(x). In fact, it is the reciprocal of the sine function, meaning that y = csc(x) = 1/sin(x). This kinship allows us to borrow insights from the sine function to understand the behavior of y = csc(x).

Domain, Range, and Asymptotes: Boundary Exploration

To fully grasp the contours of y = csc(x), we must explore its domain, range, and asymptotes.

Domain: Navigating the Forbidden Zones

The domain of a function represents the set of all possible input values. For y = csc(x), we have an exclusion list. The function is undefined at values of x that correspond to multiples of π/2, which are the points where the sine function in the denominator becomes zero.

Range: Unbounded Freedom

The range of a function, on the other hand, encompasses all the possible output values. In the case of y = csc(x), its range extends to all real numbers. Its graph can soar to any height or plummet to any depth, unconstrained by limits.

Asymptotes: Lines of Infinity

Asymptotes are lines that a function approaches but never quite touches. Y = csc(x) has vertical asymptotes at x = nπ/2, where n is an integer. These lines represent the points where the function tends to infinity or negative infinity. Additionally, it has horizontal asymptotes at y = -1 and y = 1.

Symmetry: A Reflection in the Origin

Y = csc(x) exhibits an odd symmetry, meaning that its graph is symmetrical with respect to the origin. When reflected across the origin, the graph remains unchanged.

Graphing the Cosecant: A Visual Symphony

To truly appreciate the beauty of y = csc(x), we must visualize its graph. It bears a striking resemblance to the graph of y = sin(x), but with a crucial distinction. Y = csc(x) is a vertical stretch of y = sin(x) by a factor of 1. This means that the peaks and troughs of y = csc(x) are more extreme, rising higher and falling lower than those of its sine counterpart.

The period of y = csc(x) is a gateway to understanding its intricate nature. By unraveling this concept and exploring the related ideas of periodic functions, amplitude, sine connection, domain, range, asymptotes, symmetry, and graphing, we gain a deeper appreciation for the beauty and complexity of this mathematical marvel. So, let us embrace the enigma of the cosecant function, for it holds within it a wealth of mathematical wonders to behold.

The Fascinating World of y = csc(x) and Its Mathematical Symphony

Ladies and gentlemen, prepare to immerse yourselves in the enchanting world of trigonometry! Today, we embark on a captivating exploration of the period of y = csc(x), a mesmerizing function that dances through a kaleidoscope of mathematical concepts.

Periodic Harmony: The Rhythm of Functions

In the realm of mathematics, periodicity reigns supreme. A periodic function is like a musical melody that repeats itself over and over again. Just as a song has a certain number of beats in each measure, a periodic function oscillates between specific values at regular intervals.

Our protagonist, y = csc(x), is a prime example of periodicity. It swings between positive and negative infinity, completing one full cycle every 2π units. This rhythmic pattern is known as its period.

A Family of Related Concepts

As we delve deeper into the world of y = csc(x), we encounter a constellation of related concepts that illuminate its unique nature.

• Amplitude: y = csc(x) has no amplitude, as it lacks well-defined maximum or minimum values. It’s like a restless wanderer, eternally ascending and descending without ever reaching a peak or trough.

• Sine Connection: Y = csc(x) is inextricably linked to its trigonometric cousin, sine. In fact, it’s the reciprocal of y = sin(x), meaning that it inverts the values of sine. This kinship grants y = csc(x) a fascinating set of properties.

Exploring the Boundaries: Domain, Range, and Asymptotes

Like a vast ocean, y = csc(x) has its own well-defined boundaries.

• Domain: It reigns over all real numbers except for multiples of π/2, where the sine function in its denominator becomes undefined. These numbers act as forbidden zones, interrupting the function’s otherwise continuous flow.

• Range: In contrast, the range of y = csc(x) is limitless. It can soar to any real number, positive or negative, as it dances across its vertical asymptotes.

• Asymptotes: Speaking of asymptotes, y = csc(x) has vertical asymptotes at x = nπ/2, where sine goes rogue. It also has horizontal asymptotes at y = -1 and y = 1, acting as invisible barriers that limit the function’s vertical movement.

Symmetry: A Mirror Image of Beauty

Y = csc(x) possesses an intrinsic symmetry, like a butterfly with perfectly balanced wings. It’s an odd function, meaning that it flips over the origin when you reflect it across the y-axis. This mirroring effect creates a captivating visual harmony.

A Visual Symphony: Unveiling the Graph

Finally, let’s feast our eyes on the graph of y = csc(x). It’s like a roller coaster ride through the mathematical landscape. You’ll see alternating peaks and valleys, a constant dance between positive and negative infinity.

Compare this graph to that of y = sin(x), and you’ll notice a striking resemblance. They’re like siblings, with y = csc(x) being a vertical stretch of y = sin(x) by a factor of 1. This visual connection further deepens our understanding of these trigonometric wonders.

So there you have it, a tantalizing glimpse into the world of y = csc(x) and its intricate mathematical tapestry. From periodicity to symmetry, from domain to asymptotes, this function is a symphony of mathematical concepts that never fails to amaze.

The Enigmatic Periodicity of the Cosecant Function (y = csc(x))

In the realm of trigonometry, functions like the cosecant (y = csc(x)) hold a captivating allure. Among their captivating traits lies the concept of periodicity, an intrinsic property that defines the function’s cyclical nature. Dive into the intriguing world of y = csc(x) as we unravel its periodicity and other fascinating concepts.

Periodicity: The Rhythmic Pattern

In the world of functions, periodicity reigns supreme, describing the tendency of a function to repeat itself over a fixed interval known as its period. For the enigmatic y = csc(x), this period measures a steadfast 2π, signifying its unwavering rhythm.

A Family Trait: The Periodic Function

Functions like y = csc(x) belong to the esteemed family of periodic functions, characterized by their penchant for repeating their patterns over regular intervals. As a member of this illustrious clan, y = csc(x) proudly displays its 2π periodicity, exhibiting its unwavering cyclical behavior.

Amplitude: An Elusive Concept

While most functions fluctuate between maximum and minimum values, y = csc(x) stands out as an exception. Its values dance endlessly across the real number line, never reaching a definitive peak or trough. Consequently, y = csc(x) has no discernible amplitude, leaving it devoid of the characteristic bounds that define many trigonometric brethren.

A Tangled Tale: The Interplay of Sine and Cosecant

The relationship between y = csc(x) and its sine counterpart, y = sin(x), is akin to a twisted tapestry, where one is the mirror image of the other. Y = csc(x) emerges as the reciprocal of y = sin(x), subtly intertwining their destinies.

Unveiling the Realm of Domain, Range, and Asymptotes

Domain: The domain of y = csc(x) encompasses all real numbers, save for those sneaky multiples of π/2. These forbidden values arise from the lurking presence of the undefined sine function in the denominator, casting a shadow over certain regions of the real number line.

Range: As a testament to its boundless nature, y = csc(x) roams freely across the entirety of the real number line, claiming all values as its own.

Asymptotes: Vertical asymptotes stand sentinel at the gates of x = nπ/2, where n is any integer, marking the points where the sine function stumbles and y = csc(x) becomes undefined. Additionally, horizontal asymptotes stretch out at y = -1 and y = 1, providing refuge for the function as it approaches these values.

Symmetry: A Reflection of Grace

Y = csc(x) embodies the essence of an odd function, displaying a graceful symmetry about the origin. Its graph mirrors itself with effortless elegance, creating a harmonious balance.

Graphing the Cosecant’s Undulations

The graph of y = csc(x) evokes a captivating dance, oscillating between positive and negative infinity. Compared to its sine counterpart, y = csc(x) stands tall, stretched vertically by a factor of 1, accentuating its periodic nature.

Describe the relationship between y = csc(x) and y = sin(x), highlighting that y = csc(x) is the reciprocal of y = sin(x).

The Enigmatic Periodicity of the Cosecant Function

In the realm of mathematical functions, the concept of periodicity holds great significance. A periodic function is one that repeats its pattern over a consistent interval known as its period. The cosecant function, denoted by y = csc(x), is no exception to this rule, exhibiting a period of 2π.

The reciprocal nature of the cosecant function is a defining characteristic that sets it apart from other trigonometric functions. As the inverse of the sine function (y = sin(x)), the cosecant function shares an intimate relationship with its counterpart. In essence, the cosecant function can be thought of as the reciprocal of the sine function, meaning that y = csc(x) = 1/sin(x).

This inherent connection between the cosecant and sine functions has profound implications for their behavior. While the sine function oscillates between -1 and 1, the cosecant function assumes all real values except for zero. Consequently, y = csc(x) possesses no amplitude, unlike its sinusoidal counterpart.

The cosecant function’s periodicity is further evidenced by its vertical asymptotes at x = nπ/2, where n is any integer. These asymptotes arise from the undefined nature of the sine function when its argument is a multiple of π/2. Additionally, the cosecant function exhibits horizontal asymptotes at y = -1 and y = 1, indicating that as x approaches infinity or negative infinity, the function approaches these values.

The cosecant function, like the sine function, is an odd function, meaning that its graph is symmetric about the origin. This symmetry arises from the fact that y = -csc(x) = -1/sin(x).

In comparing the graphs of y = csc(x) and y = sin(x), we discover a striking similarity. The cosecant function is essentially a vertical stretch of the sine function by a factor of 1. This elongation is a direct consequence of the reciprocal nature of the cosecant function.

The cosecant function finds applications in various fields, including engineering, physics, and astronomy. Its ability to model periodic phenomena, such as the motion of celestial bodies or the oscillations of springs, makes it an indispensable tool for understanding the dynamic world around us.

The Periodicity and Nature of y = csc(x)

In the realm of trigonometry, functions dance in rhythm, repeating their patterns over certain intervals called periods. One such function, the cosecant function (y = csc(x)), exhibits a defining characteristic – a period of 2π.

The Essence of Periodicity

Imagine a function as a dancer moving along a number line. As they sway and twirl, they return to their original position after a specific distance traveled. This distance, known as the period, represents the full cycle of the function’s movements. For y = csc(x), this distance is 2π.

Related Concepts and their Dalliance

Periodic Functions: Like y = csc(x), periodic functions are those that repeat their pattern after a fixed interval. Its period of 2π makes y = csc(x) a prime example of this characteristic.

Amplitude: This concept involves the maximum and minimum values a function can reach. However, for y = csc(x), the dance continues indefinitely, never reaching a peak or a low point. Hence, it has no amplitude.

Sine Function: y = csc(x) shares an intimate relationship with the sine function (y = sin(x)). They are reciprocals of each other, meaning y = csc(x) is the inverse of y = sin(x). This reciprocal nature profoundly influences their behavior.

Exploring the Boundaries

Domain: The stage on which y = csc(x) performs is restricted. As the sine function in its denominator threatens to vanish, the dance grinds to a halt at multiples of π/2. These forbidden points exclude the function’s domain.

Range: In contrast to its domain, y = csc(x) has an unbounded range, allowing it to gracefully sweep across all real numbers.

Asymptotes: Like invisible walls, vertical asymptotes mark the boundaries beyond which y = csc(x) cannot venture. These occur at x = nπ/2, where n is an integer. Additionally, horizontal asymptotes at y = -1 and y = 1 guide the function’s dance, keeping it within certain limits.

Symmetry and Graphing

Symmetry: y = csc(x) exhibits an odd symmetry, mirroring itself perfectly across the origin.

Graph: Imagine y = sin(x) standing tall. Now, stretch it vertically by a factor of 1 and you have the graph of y = csc(x). Its graceful curves ascend and descend, never quite reaching a peak or a valley, dancing in an endless cycle.

The Enigmatic Periodicity of y = csc(x): A Mathematical Journey

In the vast realm of functions, a curious character emerges: y = csc(x), a function that dances to the rhythm of a unique period. What is this period, and what other secrets does this function hold? Embark on a mathematical adventure as we unravel the mysteries of y = csc(x) and its enchanting related concepts.

The Rhythmic Periodicity

The period of a function is akin to a celestial dance, a measure of how often a pattern repeats. For our enigmatic function, this period is none other than 2π. Every time x traverses this magical interval, y = csc(x) gracefully repeats its captivating oscillations.

A Symphony of Related Concepts

Periodic Function:
y = csc(x) belongs to the illustrious family of periodic functions, functions that march rhythmically, repeating their patterns at regular intervals.

Amplitude:
Amplitude, a measure of the height or depth of oscillations, is an enigma for y = csc(x). This function possesses no maximum or minimum values, leaving it with no amplitude.

A Synapse with Sine:
y = csc(x) shares an intimate connection with its kindred spirit, y = sin(x). These functions are like two sides of the same mathematical coin, with y =csc(x) emerging as the reciprocal of y = sin(x).

Exploring the Contours of y = csc(x)

Domain:
y = csc(x) makes its home on all real numbers, except for the mischievous multiples of π/2. These forbidden zones arise from the lurking undefined sine function in the denominator.

Range:
In contrast to its elusive domain, y = csc(x) roams freely through the entire realm of real numbers.

Asymptotes:
The graph of y = csc(x) is adorned with vertical asymptotes, like ghostly sentinels standing guard at x = nπ/2, where n is an integer. The undefined sine function at these points gives rise to these vertical boundaries. Additionally, the function sways gracefully around two horizontal asymptotes, y = -1 and y = 1.

Symmetry and Artistic Appeal

y = csc(x) exhibits an elegant symmetry, mirroring its image across the origin. This odd function dances harmoniously around the x-axis.

A Visual Ode to y = csc(x)

The graph of y = csc(x) is a captivating sight, a testament to the beauty of mathematics. It resembles a graceful sinuous wave, stretching vertically from -1 to 1, with its asymptotes guiding its rhythm. The reciprocal relationship with y = sin(x) is evident in the narrower peaks and troughs of y = csc(x), enhancing its distinct visual charm.

The Period of y = csc(x) and Its Related Concepts: A Comprehensive Guide

Behold the Period

The period of a function represents the distance over which the function repeats itself. For the enigmatic y = csc(x), this period is a constant 2π. In other words, the function’s values start repeating every 2π units along the x-axis.

The Dance of Periodicity

y = csc(x) belongs to a special class of functions called periodic functions. These functions, like dancers in a graceful ballet, repeat their movements at regular intervals. The period is the distance between these repetitions.

Amplitude: A Tale of Extremes

Amplitude measures the vertical distance between the maximum and minimum values of a function. However, y = csc(x) is an anomaly. It has no maximum or minimum values, as its graph extends both upward and downward without bounds. Thus, it has no amplitude.

The Connection to Sine: A Cosmic Link

y = csc(x) and its sinusoidal counterpart, y = sin(x), share an intimate relationship. y = csc(x) is essentially the reciprocal of y = sin(x), but with a slight twist. The sine wave swings between -1 and 1, while the cosecant wave oscillates between infinity and negative infinity.

Domain, Range, and Asymptotes: The Boundaries of Existence

The domain of y = csc(x) encompasses all real numbers except for multiples of π/2. This is because the sine function in the denominator becomes undefined at these points. The range, on the other hand, knows no bounds, as y = csc(x) can assume all real numbers.

Asymptotes mark the boundaries beyond which the function cannot reach. y = csc(x) has vertical asymptotes at x = nπ/2, where n is any integer. These occur because the sine function in the denominator becomes zero at these points, making the expression undefined. Additionally, there are horizontal asymptotes at y = -1 and y = 1, representing the limits to which the function approaches as x approaches infinity and negative infinity, respectively.

Symmetry: A Reflection of Harmony

y = csc(x) exhibits a beautiful symmetry about the origin. This means that if you were to fold the graph along the y-axis, the two halves would be mirror images of each other. This symmetry stems from the odd nature of the cosecant function.

The Graph: A Visual Symphony

The graph of y = csc(x) resembles that of y = sin(x) but with a more pronounced vertical stretch. The curves are identical in shape, but y = csc(x) stretches upward and downward by a factor of 1. This stretching emphasizes the function’s unbound oscillation and its rapid changes near the vertical asymptotes.

The Enigmatic Periodicity of the Cosecant Function

In the realm of trigonometry, one encounters a captivating function: y = csc(x), the cosecant function. Its defining characteristic lies in its period, a concept that unravels the secrets of its oscillatory nature.

Defining Periodicity

Periodicity emerges as a fundamental property of functions that exhibit repetitive patterns as their input values change. For y = csc(x), its period is an awe-inspiring 2π. In other words, its graph repeats itself every 2π units along the x-axis.

Unraveling Related Concepts

Periodic Functions

Y = csc(x) proudly boasts its status as a periodic function, echoing its perpetual pattern. Its period of 2π signifies that its graph will complete a full cycle every 2π units.

Amplitude: A Case of Absence

Unlike many other periodic functions, y = csc(x) possesses an intriguing anomaly: it has no amplitude. This peculiarity stems from the absence of maximum or minimum values, resulting in an ever-changing graph that dances endlessly between infinity and negative infinity.

Sine’s Reciprocal Connection

Y = csc(x) bears an intimate relationship with another trigonometric superstar: y = sin(x). They share a profound bond, as y = csc(x) is the reciprocal of y = sin(x). This interconnectedness offers a glimpse into their shared essence.

Exploring Key Characteristics

Domain: Where the Function Reigns

Y = csc(x) gracefully resides in all the real numbers except when the denominator, sin(x), vanishes. These forbidden zones occur at multiples of π/2, which serve as vertical asymptotes.

Range: A Boundless Embrace

The range of y = csc(x) is a testament to its unyielding nature. It encompasses all real numbers, reflecting its ability to ascend to infinity and descend to negative infinity.

Asymptotes: Guiding Lights and Boundaries

Vertical asymptotes at x = nπ/2 (where n is an integer) obstruct y = csc(x) from venturing beyond these boundaries. These sentinels arise due to the undefined nature of sin(x) at these points. Horizontal asymptotes at y = -1 and y = 1 gently guide the graph’s oscillations, preventing it from unbounded excursions.

Symmetry: Reflections in the Origin

Y = csc(x) exhibits an elegant odd symmetry, mirroring itself perfectly around the origin. This symmetry attests to its balanced nature, where positive and negative values complement each other harmoniously.

Unveiling the Graph: A Visual Exploration

The graph of y = csc(x) unveils an enchanting spectacle. It resembles a vertical stretch of y = sin(x) by a factor of 1. This transformation accentuates the oscillations, creating a more pronounced waveform. The graph gracefully undulates, forever oscillating between infinity and its negative counterpart.

Compare the graph of y = csc(x) to that of y = sin(x), explaining that y = csc(x) is a vertical stretch of y = sin(x) by a factor of 1.

The Fascinating World of y = csc(x): A Dive into Its Period and Intriguing Concepts

In the world of trigonometry, there exists a captivating function known as y = csc(x). This function holds a unique characteristic known as periodicity, which defines the interval over which its values repeat. For y = csc(x), this period is an unwavering 2π.

Exploring Related Concepts

The period of a function is closely intertwined with other fundamental concepts. Periodic functions are those that consistently repeat their pattern over a specific interval, and y = csc(x) is a prime example, exhibiting its pattern every 2π units.

While y = csc(x) lacks a maximum or minimum value, it does possess an amplitude. This measure of its oscillation’s height is undefined for y = csc(x), as its values oscillate between positive and negative infinity.

Connections to the Sine Function

y = csc(x) shares a fascinating relationship with its trigonometric counterpart, y = sin(x). In fact, y = csc(x) can be expressed as the reciprocal of y = sin(x), creating a mirror image of its sinusoidal pattern.

Domain, Range, and Asymptotes

The domain of y = csc(x) encompasses all real numbers except for multiples of π/2, where the sine function in its denominator becomes undefined. Conversely, the range of y = csc(x) spans all real numbers.

As for asymptotes, y = csc(x) exhibits vertical asymptotes at x = nπ/2 (where n is an integer) due to the undefined sine function. Additionally, it features horizontal asymptotes at y = -1 and y = 1.

Symmetry

The graph of y = csc(x) displays an odd symmetry, mirroring itself across the origin. This means that for every point (x, y) on the graph, there exists a corresponding point (-x, -y).

Graph Comparison

Comparing the graphs of y = csc(x) and y = sin(x), we observe a striking similarity in their wavy patterns. However, the graph of y = csc(x) appears as a vertical stretch of the sine wave, with its amplitude stretched by a factor of 1. This stretching emphasizes the rapid oscillations of y = csc(x), which oscillate between positive and negative infinity.