Determining The Rate Law: A Comprehensive Guide For Seo Optimization
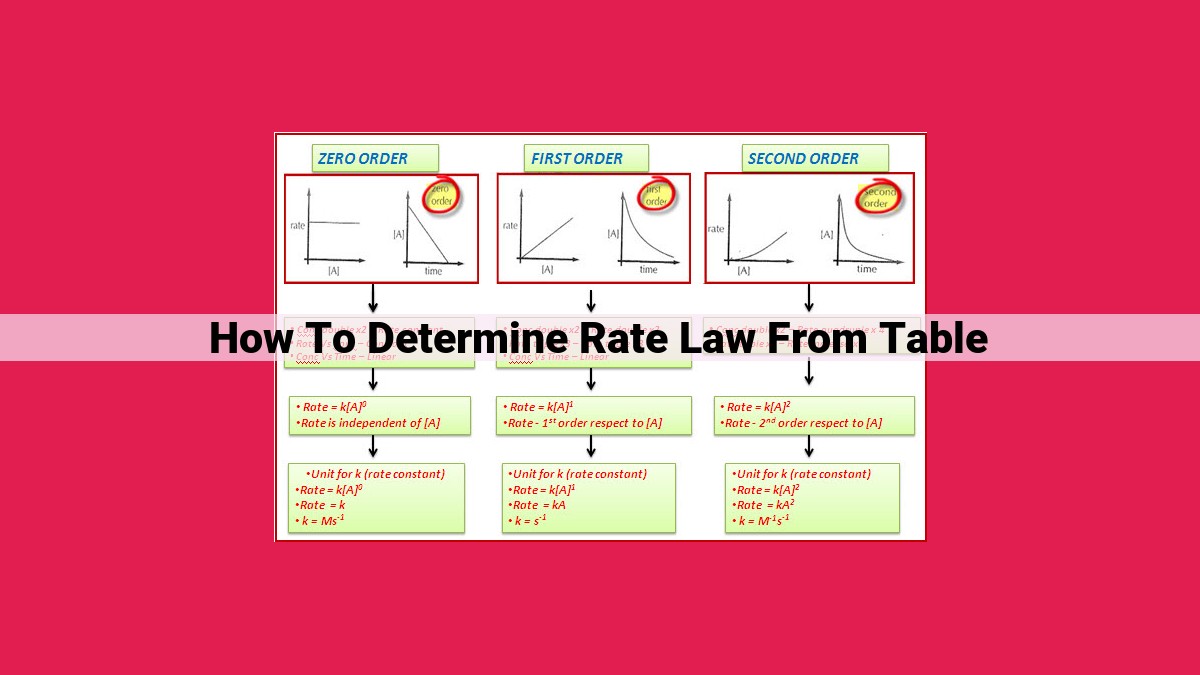
To determine the rate law from a given table, analyze the relationship between reaction rates and reactant concentrations. Determine the order of reaction for each reactant by observing how the rate changes with concentration. Utilize the mathematical form of the rate law (rate = k[A]^x[B]^y) to derive the equation from the experimental data. Identify the rate constant (k) and the exponents (x, y) that represent the reaction order. This approach allows you to accurately predict reaction rates and understand the kinetics of chemical reactions.
Unveiling the Secrets of Reaction Rates: A Comprehensive Guide to Determining Rate Laws
In the realm of chemistry, understanding the intricacies of chemical reactions is paramount. Among these crucial aspects is unraveling the relationship between reaction rates and reactant concentrations. This profound connection is captured in the enigmatic formula known as the rate law.
The rate law is a mathematical equation that quantifies the rate of a chemical reaction. It reveals how the rate of a reaction varies with the concentrations of the reactants. This invaluable tool empowers chemists to predict the speed at which reactions will proceed and to control the outcomes of complex chemical processes.
The rate law is expressed in terms of the order of reaction with respect to each reactant. The order of reaction dictates how the reaction rate changes in response to changes in reactant concentrations. If a reaction is first order with respect to a particular reactant, for instance, doubling the concentration of that reactant will double the reaction rate.
Determining the rate law is crucial for comprehending reaction kinetics, the study of the rates of chemical reactions. This knowledge opens doors to predicting the half-life of a reaction, the time it takes for the concentration of a reactant to halve. With this information, chemists can design experiments with precise timing to achieve desired outcomes.
The journey to determining rate laws begins with experimental data. By measuring the concentrations of reactants and products over time, chemists can extract valuable information about the reaction’s kinetics. This data can then be analyzed using various techniques to derive the rate law.
Once the rate law is established, it becomes a powerful tool for understanding the reaction mechanism and predicting future behavior. Chemists can use this knowledge to optimize reaction conditions, maximize yields, and minimize unwanted side reactions. It also enables them to delve into the intricacies of complex chemical systems, unlocking the secrets of their dynamic behavior.
Concepts Involved in Determining Rate Laws
In the realm of chemical kinetics, understanding rate laws is essential for predicting the behavior of chemical reactions. Rate laws dictate the relationship between the reaction rate and the concentrations of the reactants. To delve deeper into this intriguing concept, let’s explore some key concepts:
Order of Reaction
The order of reaction reveals the dependency of the reaction rate on the concentration of each reactant. For instance, a reaction that doubles its rate when the reactant concentration is doubled is said to be first order. Conversely, if the rate triples, it’s second order.
Integrated Rate Laws
Integrated rate laws are mathematical equations that express the relationship between the reactant concentrations and the time required for the reaction to reach a certain point. These equations can be derived from the rate law and take various forms depending on the order of reaction.
Half-Life
The half-life of a reaction is the time it takes for the reactant concentration to decrease by half. This concept is particularly useful for predicting the longevity of a reaction and its potential applications.
Mathematical Relationships
These concepts are intricately connected by mathematical relationships. The order of reaction determines the form of the integrated rate law, which in turn allows us to calculate the half-life. Understanding these relationships is crucial for interpreting and predicting the behavior of chemical reactions accurately.
Rate Law: Formulation and Interpretation
In the fascinating world of chemical kinetics, rate laws play a pivotal role in unraveling the secrets of how reactions unfold. Determining the rate law of a reaction involves constructing a mathematical equation that describes the relationship between the reaction rate and the concentrations of reactants. This equation provides a snapshot of the reaction kinetics, allowing us to predict how the reaction will progress.
The rate law takes the general form:
Rate = k[A]^m[B]^n
where:
- Rate is the change in concentration of products or reactants over time
- k is the rate constant, a proportionality factor that reflects the intrinsic reactivity of the reaction
- [A] and [B] are the concentrations of reactants A and B, respectively
- m and n are the orders of reaction for reactants A and B, respectively
The order of reaction is an exponent that indicates the power to which the reactant concentration is raised in the rate law. It reflects the dependence of the reaction rate on that reactant.
The rate constant is a temperature-dependent parameter that is unique to a specific reaction and is determined experimentally. It provides insight into the activation energy of the reaction, or the minimum energy required for the reaction to occur.
By carefully analyzing experimental data, scientists can determine the rate law of a reaction. This process involves measuring the reaction rate under various conditions, such as varying the initial concentrations of reactants. The experimental data is then plotted and analyzed to extract the values of the rate constant and the orders of reaction.
Example: Consider the reaction between hydrogen and iodine:
H2(g) + I2(g) -> 2HI(g)
By conducting a series of experiments and analyzing the data, it is found that the rate law for this reaction is:
Rate = k[H2][I2]
This rate law indicates that the reaction is first order with respect to both hydrogen and iodine. This means that the reaction rate is directly proportional to the concentrations of both reactants. The rate constant for this reaction reflects the intrinsic reactivity of hydrogen and iodine and the activation energy required for the reaction to proceed.
Integrated Rate Laws: Unveiling the Dynamics of Chemical Reactions
Integrated rate laws provide a powerful tool for unlocking the intricacies of chemical reactions. They allow us to predict the concentration of reactants or products over time, enabling us to gain invaluable insights into the kinetics of a reaction.
Forms of Integrated Rate Laws:
The form of an integrated rate law depends on the order of the reaction, which indicates the exponent to which the concentration of each reactant is raised. Here are the different forms for common reaction orders:
- Zero-order:
Integrated Rate Law = -kt + [A]0 - First-order:
ln[A] = -kt + ln[A]0 - Second-order:
1/[A] = kt + 1/[A]0
Derivation of Integrated Rate Laws:
Integrated rate laws can be derived from the differential rate law using calculus techniques. For example, for a first-order reaction, the differential rate law is d[A]/dt = -k[A]. Integrating this equation gives the integrated rate law ln[A] = -kt + C, where C is a constant.
Half-Life: A Practical Application:
A particularly useful application of integrated rate laws is the determination of half-life. Half-life is the time required for the concentration of a reactant to decrease to half of its initial value. For a first-order reaction, the half-life is given by the equation t1/2 = ln(2)/k. Knowing the half-life provides valuable information about the rate of a reaction.
Integrated rate laws empower us to understand the time-dependent behavior of chemical reactions. They provide essential tools for predicting concentration changes, assessing reaction rates, and gaining a deeper understanding of the dynamics of chemical processes. By harnessing the power of integrated rate laws, we can unlock the secrets of chemical kinetics and advance our knowledge of the molecular world.
Experimental Data: Collection and Analysis
- Emphasize the importance of experimental data in determining rate laws.
- Describe various experimental techniques used to collect reaction data.
- Explain how to analyze experimental data to extract rate law information.
Experimental Data: The Key to Unlocking Rate Laws
To accurately determine rate laws, experimental data is paramount. Chemists employ various techniques to collect this data, each providing crucial insights into reaction kinetics.
One common method is to measure the concentration of reactants or products over time. Spectrophotometry, a technique that measures light absorption, can precisely quantify the concentration of colored reactants or products. For instance, in the Belousov-Zhabotinsky reaction, a complex chemical oscillator, spectrophotometry reveals the periodic oscillations in concentrations of the various reactants and products.
Another technique is to monitor the rate of gas evolution. In reactions that produce gases, such as the decomposition of hydrogen peroxide, the rate of gas release can be measured using a gas burette or a pressure sensor. This data provides insights into the rate at which reactants are consumed and products are formed.
Once experimental data is collected, it must be analyzed to extract rate law information. This involves plotting the concentration or pressure data against time, then applying mathematical techniques to determine the order of reaction and rate constant.
For example, in a first-order reaction, the concentration of the reactant decreases exponentially with time. Plotting the natural logarithm of the concentration against time yields a straight line whose slope gives the rate constant. In contrast, for a second-order reaction, the inverse of the concentration is plotted against time, and the slope of the line provides the rate constant.
By carefully analyzing experimental data, chemists can determine the rate laws for specific reactions. These rate laws provide valuable information about the reaction mechanisms, allowing scientists to predict reaction rates and outcomes under different conditions.
Initial Concentrations: The Key Player in Reaction Rates
The Intimate Connection Between Concentration and Reaction Speed
Just like in life, initial conditions can have a profound impact on the outcome of any endeavor. The same goes for chemical reactions. The initial concentrations of the reactants play a crucial role in determining how fast a reaction will proceed.
Unveiling Initial Concentrations: From Data to Understanding
Initial concentrations are like the starting point of a reaction. They can be determined from experimental data or provided in tables. These values give us valuable insights into how a reaction will behave.
Initial Concentrations: The Driving Force of Reaction Kinetics
The initial concentrations of reactants have a direct bearing on reaction kinetics, the branch of chemistry that studies the rates of chemical reactions. Higher initial concentrations mean more reactant molecules are available to interact, resulting in a faster reaction.
For example, consider the reaction between hydrogen (H2) and iodine (I2) to form hydrogen iodide (HI):
H2 + I2 → 2HI
If we increase the initial concentration of either H2 or I2, the reaction rate will increase because there are more reactant molecules colliding and reacting.
Harnessing Initial Concentrations for Optimal Reaction Outcomes
Understanding the impact of initial concentrations is essential for controlling and optimizing chemical reactions. In industrial settings, this knowledge can lead to more efficient processes and improved product yields. For instance, in the production of pharmaceuticals, adjusting initial concentrations can minimize side reactions and enhance the desired outcomes.
By unraveling the relationship between initial concentrations and reaction rates, we gain a powerful tool for predicting and controlling chemical reactions. This knowledge forms the cornerstone of effective chemical engineering and opens doors to advancements in numerous scientific fields.
Case Studies and Examples
- Provide specific examples of how to determine rate laws from tables.
- Analyze real-world reaction data and interpret the results.
Case Studies and Examples: Determining Rate Laws from Tables
In the realm of chemical kinetics, tables play a pivotal role in unlocking the secrets of chemical reactions. By scrutinizing tables that chronicle the concentrations and reaction rates over time, scientists can piece together the puzzle of how reactions unfold.
Consider the following experimental data for a reaction between A and B:
| Time (s) | [A] (M) | [B] (M) | Rate (M/s) |
|---|---|---|---|
| 0 | 1.0 | 0.5 | 0.2 |
| 10 | 0.75 | 0.375 | 0.15 |
| 20 | 0.5 | 0.25 | 0.1 |
| 30 | 0.25 | 0.125 | 0.05 |
Our mission is to determine the rate law for this reaction. By analyzing the data in the table, we notice a pattern: the reaction rate is directly proportional to the concentration of A and squared the concentration of B. This leads us to the following rate law:
Rate = k[A][B]^2
In this rate law, k represents the rate constant, a numerical value that reflects the inherent tendency of the reaction to occur. By determining the rate law, we gain insight into the reaction mechanism and the relative strengths of the reactant concentrations in influencing the reaction rate.
Another example involves a pseudo-first-order reaction, where one of the reactants is in large excess compared to the other. In such cases, the concentration of the excess reactant remains virtually constant, and the reaction exhibits first-order kinetics with respect to the other reactant.
By understanding rate laws, we can predict reaction rates under various conditions, design experiments, and optimize chemical processes. Rate laws are indispensable tools that empower scientists to harness the intricacies of chemical kinetics for solving real-world problems and advancing our understanding of the molecular world.
Applications and Future Directions of Rate Laws
Practical Applications in Chemistry
Rate laws play a crucial role in various chemical industries and applications. In environmental chemistry, they help predict the rate of pollutant degradation and design effective remediation strategies. In the pharmaceutical industry, rate laws guide the optimization of drug synthesis and dosage regimens to ensure maximum efficacy and safety. Furthermore, in materials science, rate laws aid in developing new materials with tailored properties by controlling reaction rates during fabrication.
Ongoing Research and Advancements
The field of chemical kinetics continues to evolve, fueled by advancements in experimental techniques and theoretical modeling. Current research focuses on developing sophisticated experimental methods to measure reaction rates with high precision and accuracy. These methods allow for the study of complex reactions and the identification of fleeting intermediates.
Moreover, computational modeling is emerging as a powerful tool for predicting rate laws and exploring reaction mechanisms. By simulating reactions at the molecular level, researchers can gain insights into the microscopic processes that dictate reaction rates. This knowledge can guide the design of new catalysts and the development of more efficient chemical processes.
Future Directions
The future of chemical kinetics holds exciting prospects. Researchers are exploring the use of machine learning to analyze experimental data and extract rate laws. This approach has the potential to automate the determination of rate laws for complex reactions and accelerate the discovery of new kinetic models.
Additionally, the development of microfluidic devices is enabling the study of reactions under highly controlled conditions. These devices allow for the precise manipulation of reactants and the measurement of reaction rates in real time. This capability opens new avenues for investigating the kinetics of nanoscale reactions and understanding the behavior of chemical systems in confined environments.
By embracing these advancements, chemical kinetics will continue to drive innovations in various fields, from the design of new materials and pharmaceuticals to the understanding of complex environmental processes.