Determine Y-Intercept Of Linear Equations: Slope-Intercept And Two-Point Methods

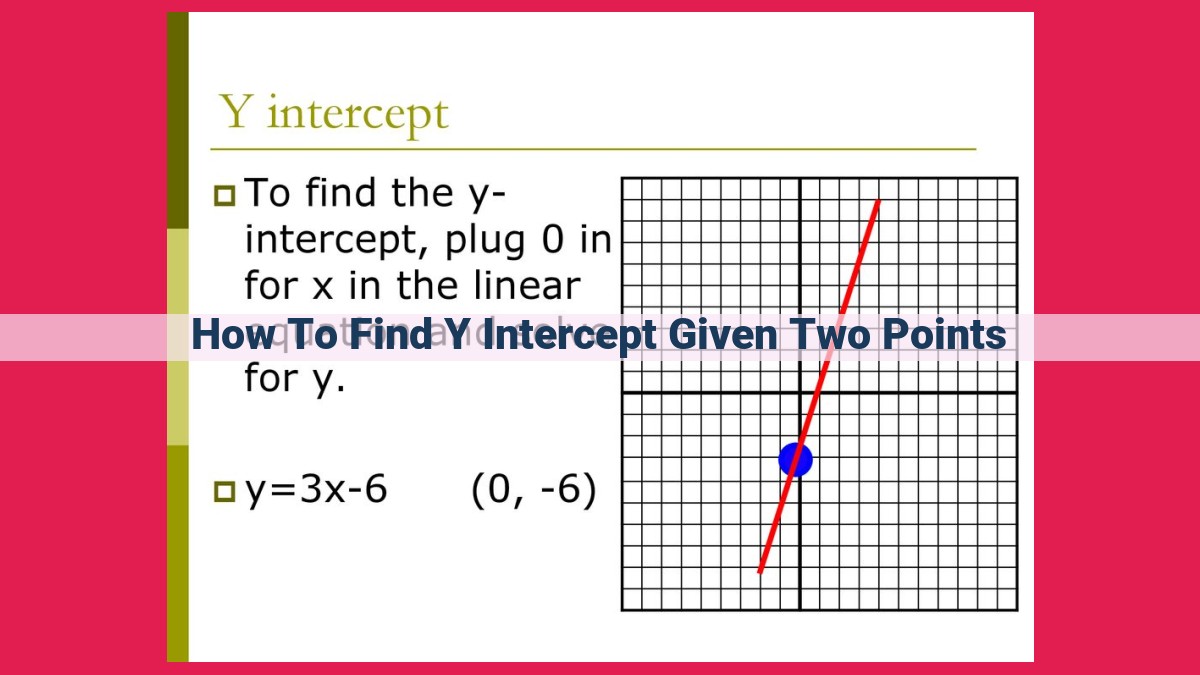
To determine the y-intercept of a linear equation, utilize slope-intercept form (y = mx + c) or two-point form. To find the y-intercept using the slope-intercept form, set x to 0 and solve for c. In two-point form, substitute the points (x1, y1) and (x2, y2), set x to 0, and solve for y. For instance, given (2, 5) and (-1, 2), use the two-point form: (y – y1)/(x – x1) = (y2 – y1)/(x2 – x1). Substitute y1 = 5, x1 = 2, y2 = 2, and x2 = -1, and set x = 0 to get the y-intercept.

Unveiling the Significance of the Y-Intercept in Linear Equations

Linear equations play a pivotal role in mathematics and are widely used in various fields, including physics, engineering, and economics. Understanding these equations requires a comprehensive grasp of the y-intercept, a crucial point where the line representing the equation crosses the y-axis.

The y-intercept is the value of the dependent variable (y) when the independent variable (x) is zero. Geometrically, it represents the point on the y-axis where the line intersects, providing valuable information about the equation’s behavior. By identifying the y-intercept, we gain insights into the equation’s positioning, slope, and overall shape.

Understanding the Y-Intercept in Slope-Intercept Form

In the realm of linear equations, the y-intercept holds a pivotal role in unraveling the secrets of these mathematical expressions. Grasping its significance empowers us to decipher the equation’s behavior and make informed deductions.

Slope-Intercept Form: A Gateway to the Y-Intercept

The slope-intercept form is a canonical representation of a linear equation, given by the equation y = mx + c. This form is a window into the equation’s characteristics, with m representing the slope and c playing the crucial role of the y-intercept.

The y-intercept is the point where the line described by the equation intersects the y-axis. In other words, it tells us the value of y when x is zero. This pivotal point provides insights into the line’s position and behavior.

Unveiling the Y-Intercept from Slope-Intercept Form

To determine the y-intercept from the slope-intercept form, we simply set x to zero and solve for y. For instance, given the equation y = 2x + 3, setting x to zero yields:

y = 2(0) + 3
y = 3

Therefore, the y-intercept for this equation is 3. This means that the line intersects the y-axis at the point (0, 3).

The Y-Intercept: A Valuable Tool in Equation Analysis

Understanding the y-intercept is not merely an academic exercise; it has practical implications in analyzing linear equations. This key parameter:

• Pinpoints the line’s vertical position: The y-intercept tells us how far up or down the line is from the origin on the y-axis.
• Supports graphing: When plotting a linear equation on a graph, the y-intercept is the starting point from which the line can be drawn.
• Facilitates equation comparison: Comparing the y-intercepts of different linear equations helps determine their relative positions and potential intersections.

In essence, the y-intercept is an indispensable piece of information that enriches our understanding of linear equations. By mastering this concept, we unlock a deeper comprehension of these mathematical expressions and their applications.

Unveiling the Secrets of the Two-Point Form: A Guide to Finding the Y-Intercept

In the realm of linear equations, the y-intercept plays a crucial role in understanding the graph’s behavior. It is the point where the line intersects the y-axis, providing valuable insights into the equation’s slope and position. In this article, we will delve into the two-point form as a method to uncover the elusive y-intercept.

The two-point form is a clever formula that connects two given points on a line, denoted as (x1, y1) and (x2, y2). It is derived from the fundamental slope formula:

slope = (y2 - y1) / (x2 - x1)

The two-point form is then obtained by solving for one of the variables, typically y:

y - y1 = (y2 - y1) / (x2 - x1) * (x - x1)

If you find this formula a bit overwhelming, don’t worry! It’s a concise expression that simply states that the difference between the y-coordinates of the two points is proportional to the difference between their x-coordinates.

By setting x = 0 in this equation, we eliminate the contribution of the x-coordinate to the equation. This gives us an expression that is independent of x and simplifies to:

y = y1 - (y2 - y1) / (x2 - x1) * x1

This simplified equation is the two-point form of the linear equation. As you can see, the term y1 represents the y-intercept, the point where the line crosses the y-axis. The other terms, (y2 – y1) and (x2 – x1), are determined by the given points.

Understanding the two-point form and its connection to the y-intercept is essential for solving a wide range of linear equation problems. In the next section, we’ll dive into an example to illustrate how it works in practice.

Unveiling the Y-Intercept: A Key to Linear Equations

In the realm of mathematics, linear equations are ubiquitous. Understanding their behavior and solving them effectively hinges on a crucial parameter known as the y-intercept. This pivotal concept unlocks a deeper comprehension of linear functions and their applications.

The Y-Intercept: A Guiding Star

Imagine walking along a straight path that represents a linear equation. The y-intercept is the point where this path intersects the vertical axis, or y-axis. It pinpoints the starting value of the function before any changes occur. Knowing the y-intercept provides valuable insights into the line’s behavior and helps unravel the equation’s secrets.

Slope-Intercept Form: A Convenient Representation

Linear equations are often expressed in slope-intercept form, which takes the shape:

y = mx + c

In this equation, “m” represents the slope, describing the steepness of the line, while “c” is the enigmatic y-intercept. In slope-intercept form, the y-intercept is revealed as the constant term “c”.

Two-Point Form: A Different Perspective

Another way to represent linear equations is through the two-point form:

y - y1 = (y2 - y1) / (x2 - x1) * (x - x1)

Here, the y-intercept is embedded within the numerator of the fraction, making it less apparent at first glance. However, by setting x equal to zero, the two-point form transforms into “y1 = c”, where c represents the y-intercept.

Unlocking the Secrets of Linear Equations: A Journey to Find the Y-Intercept

In the realm of mathematics, linear equations hold a pivotal role. They allow us to describe relationships between variables, predict outcomes, and model real-world phenomena. Amidst this equation landscape, the y-intercept stands out as a beacon of significance, providing crucial information about the equation’s behavior.

Understanding the y-intercept is paramount for fully comprehending linear equations. It is the point where the line represented by the equation intersects the y-axis, the vertical axis in a coordinate plane. In essence, it tells us where the line begins when we start tracing it upward from the origin.

Slope-Intercept Form: A Gateway to Interception

One of the most prevalent forms of linear equations is the slope-intercept form, denoted as y = mx + c. In this equation, “m” represents the slope, the measure of the line’s steepness, and “c” is the y-intercept. The role of “c” as the y-intercept is evident in its placement at the end of the equation, without the inclusion of “x.” This implies that when “x” is equal to zero, the value of “y” is equal to “c,” which is precisely the y-intercept.

Two-Point Form: A Different Path to Y-Intercept

Beyond slope-intercept form, another route to finding the y-intercept is through the two-point form. Derived from the slope formula, this form takes the following shape: (y – y1) / (x – x1) = (y2 – y1) / (x2 – x1). Here, (x1, y1) and (x2, y2) represent two distinct points on the line.

To utilize this form, simply set “x” to zero. This action eliminates the “x” term from the numerator on the left side of the equation, leaving the y-intercept, (y1 – c). Solving for “c” then yields the desired value of the y-intercept.

Example: A Numerical Quest for the Y-Intercept

Let’s embark on a practical example to solidify our understanding. Consider the following linear equation in two-point form: (y – 2) / (x – 1) = (5 – 2) / (3 – 1). To find the y-intercept, we set “x” to zero:

(y - 2) / (0 - 1) = (5 - 2) / (3 - 1)

Simplifying the left side of the equation, we get:

y - 2 = 3

Solving for “y,” we arrive at the y-intercept:

y = 5

Therefore, the y-intercept of the given linear equation is 5.

The y-intercept carries immense significance in the world of linear equations. It provides a foundational point from which the line extends, enabling us to interpret the equation’s behavior and make accurate predictions. Whether through the slope-intercept form or the two-point form, understanding the y-intercept is a crucial step toward mastering the intricacies of linear equations.