Discover The Secret: Determining The Slope Of A Parallel Line
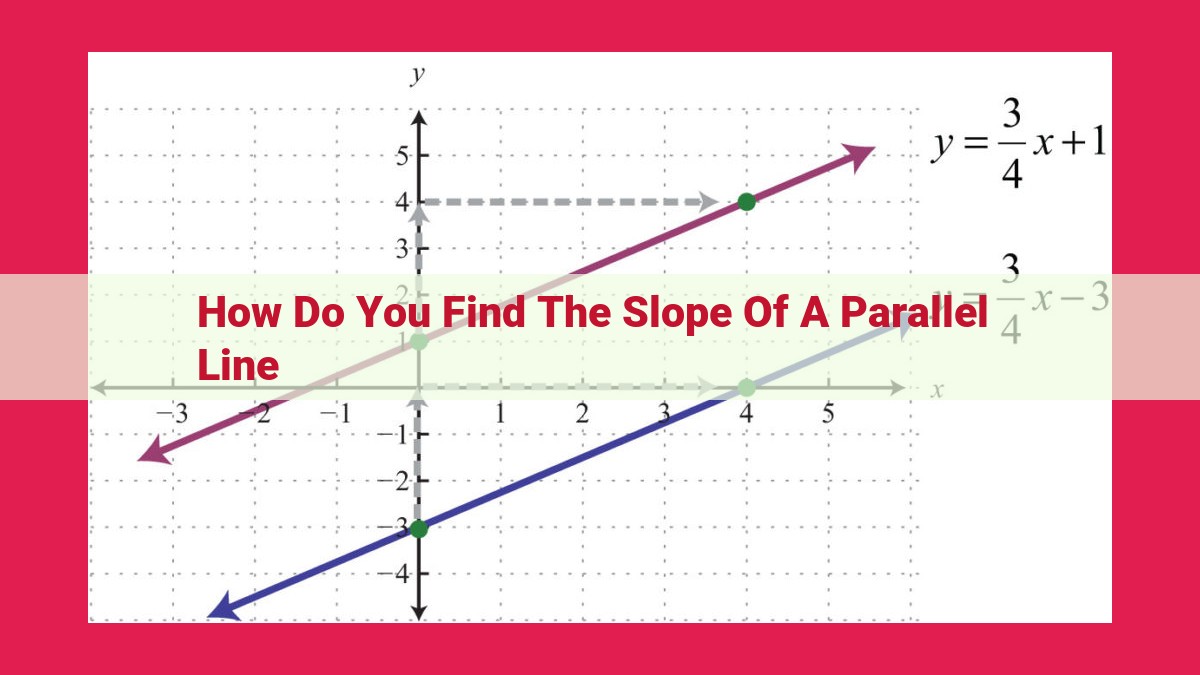
To find the slope of a line parallel to a given line with a known slope, simply use the same slope. Parallel lines have equal slopes, so the slope of the parallel line will be identical to that of the given line. Remember that the slope is a measure of the line’s steepness and is calculated as the ratio of the change in y-coordinates (vertical change) to the change in x-coordinates (horizontal change) along the line.
Parallel Lines and the Tale of the Slope
In the realm of geometry, we encounter a fascinating concept called parallel lines. Parallel lines are like spirited travelers who never cross paths, maintaining a constant distance from each other. They share some intriguing geometric properties that make them a captivating topic to explore.
One of the key characteristics that define parallel lines is their slope. Slope is a numerical value that measures the inclination of a line. It’s like a line’s fingerprint, providing a unique identifier that distinguishes it from others. The slope of a line is calculated by finding the ratio of the change in vertical distance to the change in horizontal distance.
The relationship between slope and parallelism is both intriguing and intuitive. Parallel lines, by virtue of their unwavering distance, share the same slope. Think of them as twin siblings, identical in their inclination. This shared slope acts as a bond that keeps them forever parallel.
So, there you have it, the enchanting intersection of parallel lines and slope. Understanding this concept is like unlocking a secret code that unveils the hidden stories behind geometric figures.
Slope: Measuring Line Steepness
In the realm of geometry, lines can tell intriguing stories. They can run side-by-side, never meeting, or they can intertwine to form intricate patterns. One fundamental concept that helps us understand lines is their slope.
Slope is a measure of how steeply a line rises or falls. It’s like a numerical description of a line’s inclination, telling us how much it departs from the horizontal.
To calculate slope, we use a simple formula: m = (y2 – y1) / (x2 – x1). This formula involves two points on the line, with (x1, y1) representing the starting point and (x2, y2) the ending point.
The rise is the vertical difference between the two points, while the run is the horizontal difference. Slope is calculated by dividing the rise by the run.
Slope provides valuable insights into a line’s behavior. A positive slope indicates that the line rises as it moves from left to right, while a negative slope tells us it falls. The greater the slope’s absolute value, the steeper the line.
Understanding slope is essential for analyzing linear equations and graphs. It allows us to describe the steepness of rooftops, the incline of roads, and the gradient of curves. By grasping slope’s significance, we can decipher the hidden stories behind the lines that shape our world.
Identifying Slopes of Parallel Lines
Meet the Parallel Players
In the realm of geometry, parallel lines share a special bond—they’re always in sync. Picture two roads running side by side, never crossing paths. That’s parallelism in action! And guess what? Slope, the measure of a line’s inclination, plays a crucial role in identifying parallel lines.
Slope: The Line’s Telling Angle
Slope reflects the steepness of a line. It’s calculated by dividing the vertical change (rise) by the horizontal change (run). Think of it as the line’s personal GPS, guiding it up or down the coordinate plane.
Parallel Lines: United in Slopes
Here comes the key: parallel lines have equal slopes. This means that their slopes are like identical twins, always matching. Why? Because parallel lines share the same angle of inclination. Imagine two parallel roads climbing a hill at the same slant—their slopes will be the same.
Unveiling Slopes of Parallel Lines
Let’s say you have two given lines, L1 and L2, and you know the slope of L1. To find the slope of L2, just grab the slope of L1 and give it a copy-paste. It’s that simple! Parallel lines have a shared slope; they’re like two peas in a pod.
So, when you’re dealing with parallel lines, remember their secret handshake: equal slopes. It’s a handy tool for identifying these parallel players and understanding the angles they make with the horizontal.
Determining the Slope of a Parallel Line
In geometry, parallel lines are two lines that never intersect. They maintain a consistent distance from each other and share a common property: equal slopes. Understanding how to determine the slope of a parallel line is essential for solving various geometric problems.
Step 1: Find the Slope of the Given Line
To find the slope of a parallel line, we first need the slope of a given line. The slope (m) of a line is calculated using the formula:
m = (y2 - y1) / (x2 - x1)
Where (x1, y1) and (x2, y2) are the coordinates of any two distinct points on the line.
Step 2: Principle of Equal Slopes
The key principle to remember is that parallel lines have equal slopes. Therefore, the slope of the line parallel to the given line will be the same as the slope of the given line.
Step 3: Determine the Slope of the Parallel Line
Since we know the slope of the given line, the slope of the parallel line is automatically determined. It will be the same numerical value, regardless of the positioning or orientation of the parallel line.
Example:
Consider a line with the equation y = 2x + 5. To find the slope of a line parallel to it, we simply need to extract the slope from the equation. In this case, the slope is 2. Therefore, any line parallel to y = 2x + 5 will also have a slope of 2.
Determining the slope of a parallel line is straightforward. By finding the slope of the given line and applying the principle of equal slopes, we can quickly determine the slope of any line parallel to it. This understanding is crucial for various geometric calculations and applications.