How To Determine The Height Of A Trapezoid: A Comprehensive Guide
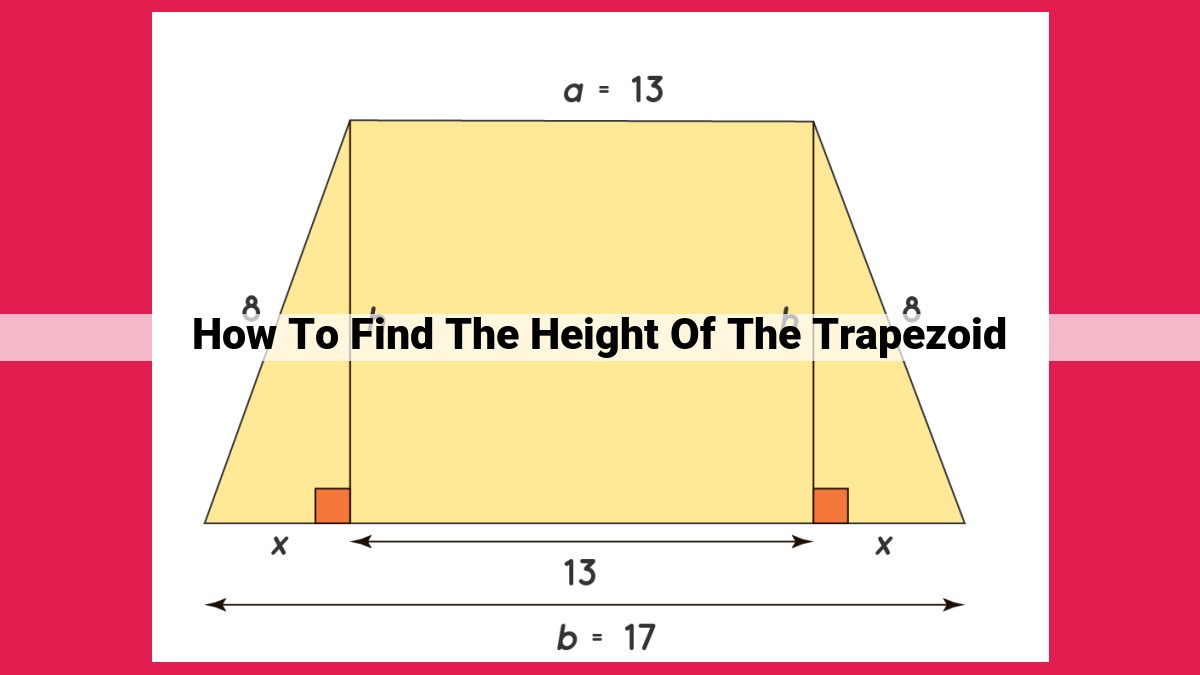
To determine the height of a trapezoid, start by identifying the bases (parallel sides) and height (perpendicular distance between the bases). Calculate the area of the trapezoid using the formula (1/2) * (sum of bases) * height. With the known area and base lengths, you can find the height using the formula: height = 2 * area / (sum of bases). Alternatively, use the Pythagorean theorem or trigonometric ratios based on the available information about angle measures or side lengths. For similar trapezoids with known height ratios, you can calculate the height proportionally.
Unlocking the Secrets of Trapezoid Heights: A Journey of Geometric Discovery
Have you ever gazed upon a trapezoid and wondered, “What mysteries lie beneath its tilted sides?” In the realm of geometry, this enigmatic quadrilateral holds the key to unlocking secrets that shape our world. Embark on an adventure to uncover the allure of trapezoids and master the art of finding their elusive height.
At its core, a trapezoid is defined by its unique shape. Imagine a quadrilateral with two parallel sides called the bases, while the other two non-parallel sides are the legs. Unlike rectangles or squares, the legs of a trapezoid have a playful slant, giving it a distinct trapezoidal flair.
Unveiling the significance of height, we delve into the realm of real-world applications. Whether designing a sturdy bridge or calculating the volume of a trapezoidal prism, knowing its height is crucial. Height governs the area of the trapezoid, acting as a gatekeeper to this geometric treasure. Without it, our calculations would falter, leaving us lost in a labyrinth of imprecise measurements.
Like intrepid explorers, we delve into the heart of trapezoid fundamentals. Bases and height form an inseparable trio, their relationship governed by the laws of geometry. We discover that the height perpendicularly bisects the bases, creating a perfect balance of symmetry. Understanding this geometric dance lays the foundation for our quest to conquer the elusive height.
Trapezoid Fundamentals: Unveiling the Building Blocks of Geometric Harmony
In the realm of geometry, trapezoids emerge as captivating shapes, characterized by their unique combination of parallel and non-parallel sides. Their versatility extends across various applications, ranging from architecture to engineering. To fully grasp the essence of trapezoids, let’s delve into their fundamental structure and explore the intricate relationship between their bases and height.
Deconstructing the Trapezoid: Bases and Height
A trapezoid is a quadrilateral with one pair of parallel sides, aptly named the bases. These bases, denoted as b1 and b2, determine the length from one end of the trapezoid to the other. The height (h), on the other hand, is the perpendicular distance between the bases, effectively connecting them at right angles.
The Symbiotic Relationship between Bases and Height
The bases and height of a trapezoid are intertwined in a mutually dependent relationship. The area (A) of a trapezoid is elegantly expressed as the product of half the sum of the bases (1/2 * (b1 + b2)) and the height (h):
A = 1/2 * (b1 + b2) * h
This formula underscores the fact that the height plays a pivotal role in determining the area of the trapezoid. By adjusting the height, you effectively alter the area. Conversely, if you know the area and the bases, you can deftly solve for the height.
In essence, the bases and height of a trapezoid are interconnected, their values influencing each other to create a cohesive geometric entity. Understanding this relationship empowers us to unravel the mysteries of trapezoids and their practical applications.
Calculating the Height of a Trapezoid from Its Area
In the intriguing world of geometry, trapezoids stand as fascinating shapes with unique properties. Understanding how to find their height is essential for unlocking the secrets they hold. One effective method involves utilizing the area formula, which provides a direct pathway to determining this crucial dimension.
The area of a trapezoid is given by the formula:
A = (1/2) * (b1 + b2) * h
where:
- A represents the area of the trapezoid
- b1 and b2 symbolize the lengths of the two parallel bases
- h signifies the height, the distance between the parallel bases
To derive the formula for calculating the height, we can rearrange the area formula as follows:
h = (2 * A) / (b1 + b2)
This modified formula empowers us to determine the height directly from the known values of the trapezoid’s area and base lengths.
Armed with this formula, we can confidently navigate a variety of geometrical challenges involving trapezoids. Whether it’s calculating the height of a painted ceiling or determining the volume of a trapezoidal prism, this method provides a reliable and precise solution.
Using the Pythagorean Theorem to Find the Height of a Trapezoid
In the realm of geometry, understanding the height of a trapezoid is crucial for solving a myriad of problems. While there are several methods to determine this elusive measurement, the Pythagorean theorem, a cornerstone of geometric knowledge, offers a powerful tool for our trapezoidal endeavors.
Trapezoids, those fascinating shapes with their parallel bases and non-parallel sides, can be cleverly dissected to form a right triangle. This right triangle, nestled within the trapezoid’s embrace, holds the key to unlocking its height.
To forge this right triangle, draw a perpendicular line from one vertex of one base to the opposite base. This line splits the trapezoid into a rectangle and a right triangle. The altitude of the trapezoid, the elusive height we seek, corresponds to the height of the right triangle.
Now, let’s invoke the illustrious Pythagorean theorem: c² = a² + b², where c is the length of the hypotenuse, and a and b are the lengths of the legs of the right triangle. In our trapezoidal realm, the hypotenuse is the diagonal of the trapezoid, while the legs are the altitude (height) and the base of the right triangle formed by our clever dissection.
So, with our Pythagorean wizardry, we can solve for the height (altitude) of the trapezoid:
Height² = Diagonal² - Base²
Height = √(Diagonal² - Base²)
This formula empowers us to determine the height of any trapezoid, unraveling its geometric secrets with mathematical precision. So, embrace the Pythagorean theorem as your guide, and conquer the challenge of finding the height of trapezoids with ease!
Using Trigonometric Ratios to Find Trapezoid Height
Defining the Trapezoid
A trapezoid is a quadrilateral with two parallel sides called bases. The non-parallel sides are called legs. The height of a trapezoid is the perpendicular distance between the bases.
Relevance of Trigonometric Ratios
Trigonometric ratios relate the sides and angles of a right triangle. In a trapezoid, we can form a right triangle by connecting a base, a leg, and a point on the other base.
Using the Sine Ratio
The sine ratio is given by:
sin(angle) = opposite / hypotenuse
In our trapezoid right triangle, we know the length of the leg opposite the angle of elevation θ and the length of the hypotenuse (which is the height h of the trapezoid).
Determining Height
To find the height h, we can use the sine ratio:
sin(θ) = leg opposite / h
Rearranging the formula:
h = leg opposite / sin(θ)
Example
Consider a trapezoid with a leg of length 5 cm and an angle of elevation of 30°.
- Leg opposite: 5 cm
- Angle of elevation: 30°
Using the sine ratio:
sin(30°) = 5 / h
h = 5 / sin(30°)
**h ≈ 6.66 cm**
Understanding the Height of Similar Trapezoids
In the realm of geometry, trapezoids hold a special place, characterized by their unique shape and versatile applications. Among their crucial dimensions, the height plays a pivotal role in determining the trapezoid’s area and other key properties. Understanding how to find the height of a trapezoid is essential for any geometry enthusiast or professional.
Similar Trapezoids: A Tale of Proportions
When two trapezoids share a striking resemblance, they are said to be similar. This means that their corresponding sides and angles are proportional. Similar trapezoids exhibit a fascinating property that allows us to determine the height of one trapezoid based on the dimensions of another.
Height Ratio: A Key to Unlocking Proportions
The height ratio between two similar trapezoids is defined as the ratio of their corresponding heights. If we denote the heights of the two trapezoids as h1 and h2, then the height ratio can be expressed as:
Height Ratio = h1 / h2
This ratio remains constant regardless of the size or orientation of the trapezoids.
Unlocking the Height of Similar Trapezoids
Imagine you have two similar trapezoids, Trapezoid A and Trapezoid B. Trapezoid A has a known height of h1, and you need to find the height of Trapezoid B (h2). Using the height ratio, you can establish the following equation:
Height Ratio = h1 / h2 = (Known Height) / h2
By rearranging this equation, you can solve for h2, the height of Trapezoid B:
h2 = (Known Height) / Height Ratio
This formula allows you to determine the height of a similar trapezoid with ease, as long as you know the height of a similar trapezoid and their height ratio.
Mastering the concepts of similar trapezoids and the height ratio empowers you to delve deeper into the fascinating world of geometry. By understanding these principles, you can confidently tackle problems involving trapezoids and determine their heights with accuracy and ease.