Unlock Cosine Values: A Guide To Reference Angles And The Pythagorean Identity

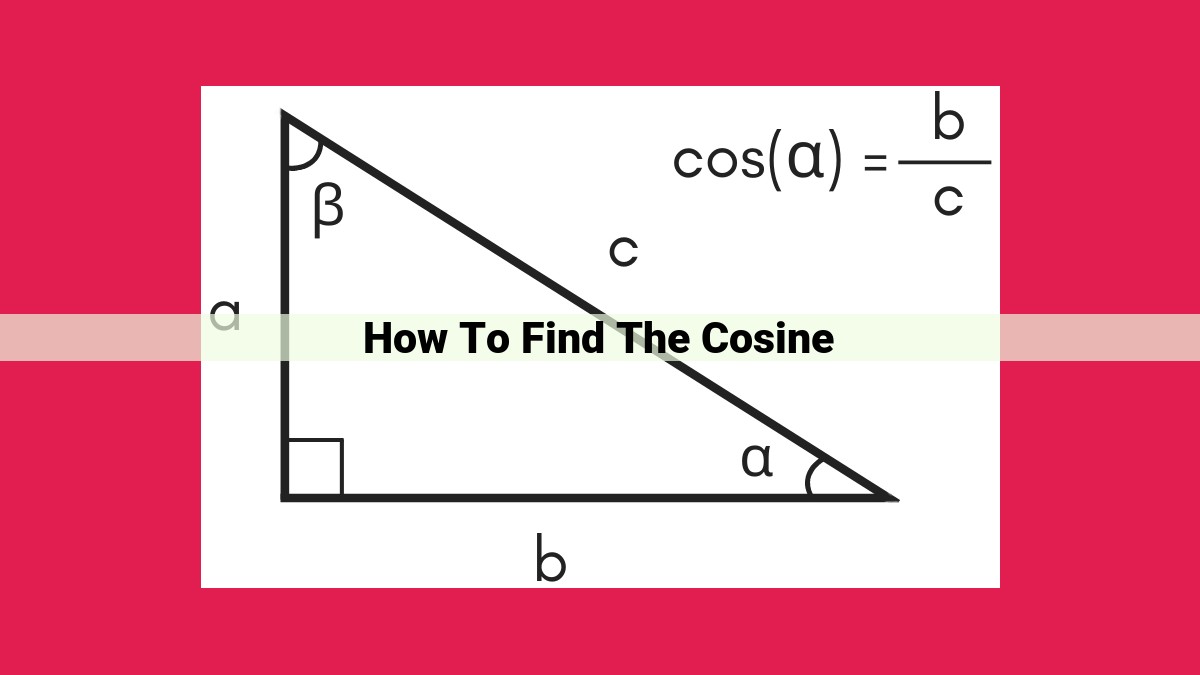
To find the cosine of an angle, determine its reference angle (the smallest positive angle formed with the x-axis). Then, use the Pythagorean identity (sin²θ + cos²θ = 1) to find the sine of the angle. The cosine is the square root of 1 minus the square of the sine. For example, to find the cosine of 60°, first find the reference angle of 30°, then use the identity to find sin(30°) = 1/2. The cosine of 60° is then √(1 – (1/2)²), which equals √3/2.

Cosine: A Comprehensive Guide to the Cornerstone of Trigonometry

In the realm of trigonometry, cosine stands as a fundamental concept that unlocks the secrets of triangles and circular motion. It is the gateway to a world of mathematical marvels, from the rhythmic oscillations of the sine wave to the intriguing symmetries of the unit circle.

Cosine: A Tricky Cousin to Sine and Tangent

Cosine is the trigonometric function that measures the ratio of the adjacent side to the hypotenuse in a right-angle triangle. Its sibling, sine, measures the ratio of the opposite side to the hypotenuse, while its mischievous cousin, tangent, represents the ratio of the opposite side to the adjacent side.

Understanding the Magic of the Unit Circle

Imagine a circle with a radius of 1, known as the unit circle. The unit circle is the magical stage where trigonometry comes alive. Cosine can be visualized as the x-coordinate of a point on the unit circle, where the angle between the positive x-axis and the line connecting the point to the center of the circle is the angle associated with the cosine.

Reference Angle: The Guiding Light

When evaluating cosine at angles greater than 360 degrees or less than 0 degrees, we need to find the reference angle, which is the acute angle between the terminal ray and the x-axis. This reference angle helps us determine the sign and magnitude of the cosine.

Sine and Cosine: A Pythagorean Love Story

Cosine and sine have a special bond known as the Pythagorean identity:

cos²θ + sin²θ = 1

This identity reveals the fundamental relationship between cosine and sine, showcasing their complementary nature.

Special Angles: A Cosine Treat

Certain angles have special cosine values that are worth memorizing:

• cos(0°) = 1
• cos(30°) = √3/2
• cos(45°) = √2/2
• cos(60°) = 1/2
• cos(90°) = 0

Cosine of Complementary Angles: A Flip of the Coin

Complementary angles add up to 90 degrees. The cosine of an angle is equal to the sine of its complementary angle. This means that cos(90° – θ) = sin(θ).

Quadrantal Angles and Cosine: A Sign of Times

Cosine changes sign in different quadrants:

• In Quadrant I, cosine is positive
• In Quadrant II, cosine is negative
• In Quadrant III, cosine is negative
• In Quadrant IV, cosine is positive

The Cosine Function: A Wave of Mathematical Elegance

When plotted as a function, cosine creates a periodic wave that oscillates between -1 and 1. The graph of the cosine function has a period of 2π and an amplitude of 1.

The Inverse Cosine Function: Undoing the Magic

The inverse cosine function (arccosine) is the mathematical opposite of cosine. It finds the angle associated with a given cosine value. The inverse cosine function is often used in applications such as navigation and surveying.

Cosine is the heart of trigonometry, providing a powerful tool for understanding triangles, circular motion, and a myriad of real-world phenomena. Whether you’re a student, engineer, or mathematician, a deep understanding of cosine will empower you to unlock the secrets of the mathematical universe.

Understanding the Unit Circle: A Gateway to Cosine

Imagine yourself standing at the center of a vast field, with a thick rope tied to a stake at its edge. As you hold onto the other end of the rope, you can swing it around, creating a circle with a radius of 1 unit. This is known as the unit circle.

The unit circle is a powerful tool that helps us visualize and understand trigonometric functions, including cosine. Cosine is a function that measures the horizontal distance from a point on the circle to the vertical axis.

To find the cosine of an angle, we start by drawing a ray from the center of the circle through the point where that angle intersects the circle. This ray will intersect the horizontal axis at a certain point. The cosine of the angle is simply the x-coordinate of this point.

For example, if we consider the angle of 30 degrees, the ray intersects the circle at a point on the positive x-axis. The x-coordinate of this point is 0.866. Therefore, the cosine of 30 degrees is 0.866.

By understanding the unit circle, we gain a deeper insight into the behavior of cosine and its relationship to other trigonometric functions. It’s like having a compass that guides us through the intricate world of trigonometry.

Finding the Reference Angle: Your Guiding Star for Cosine Mastery

As you explore the enigmatic world of trigonometry, you’ll encounter the concept of reference angles. These angles are like guiding stars, providing a clear path to understanding the intricacies of cosine.

Imagine yourself standing at the origin of a coordinate plane, with a ray extending from the origin. This ray forms an angle with the positive x-axis. The reference angle is the acute angle between this ray and the nearest x-axis, or y-axis, depending on the quadrant where the ray terminates.

Consider this example: Suppose you have an angle of 225 degrees. This angle lies in the third quadrant. To find the reference angle, we subtract 180 degrees from 225 degrees, resulting in an angle of 45 degrees. This 45-degree angle is the reference angle for 225 degrees.

Reference angles are crucial in determining the cosine of an angle. Cosine is a trigonometric function that measures the horizontal component of a right triangle. By knowing the reference angle, we can use the unit circle to determine the cosine value.

For instance, the cosine of a 45-degree angle is 1/√2. Since the reference angle for 225 degrees is 45 degrees, we know that the cosine of 225 degrees is also 1/√2.

Understanding reference angles is a fundamental step in mastering cosine. It’s like having a secret key that unlocks the mysteries of trigonometry. By embracing this concept, you’ll gain a deeper appreciation for the elegance and power of this mathematical tool.

The Intertwined Dance of Cosine and Sine: Unraveling the Pythagorean Identity

In the realm of trigonometry, cosine and sine stand as inseparable companions, their relationship intertwined through the enigmatic Pythagorean identity. This mathematical equation, a cornerstone of trigonometric understanding, unveils the profound connection between these trigonometric functions.

The Pythagorean identity, expressed as sin²θ + cos²θ = 1, establishes a harmonious balance between sine and cosine. Here, θ represents the angle of interest. This identity serves as a beacon, guiding us through the intricate tapestry of trigonometric functions.

Imagine a triangle nestled within a unit circle of radius 1. The coordinates of a point on the circle’s circumference are given by (cosθ, sinθ), where θ is the angle formed between the positive x-axis and the line connecting the point to the circle’s center.

According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In our circular setting, the hypotenuse is the radius, always measuring 1. Thus, we have:

1² = (cosθ)² + (sinθ)²

Simplifying this equation leads us to the Pythagorean identity:

sin²θ + cos²θ = 1

This identity unveils the reciprocal relationship between sine and cosine. If we know the value of one trigonometric function, we can effortlessly determine the value of the other. Moreover, this relationship allows us to navigate the trigonometric landscape with confidence.

Cosine of Special Angles: A Journey through Trigonometry’s Landmarks

In the realm of trigonometry, cosine reigns as a key player, measuring the horizontal component of a right triangle. To delve into its depths, we must navigate the mystical unit circle and uncover the secrets of special angles.

A Trip around the Unit Circle

Imagine a circle with a radius of one, where the origin serves as the center. This magical circle, known as the unit circle, is our guide to understanding the cosine function. The cosine value for an angle θ is the x-coordinate of the point on the circle corresponding to that angle.

Unveiling the Reference Angle

Before we venture further, we must grasp the concept of the reference angle. The reference angle of an angle θ is the acute angle formed between the terminal side of θ and the horizontal axis. It helps us determine the cosine value of angles beyond the first quadrant.

Sine and Cosine: A Pythagorean Union

A profound connection exists between sine and cosine, revealed by the Pythagorean identity: sin² θ + cos² θ = 1. This identity tells us that the square of the cosine of an angle, combined with the square of its sine, always equals one.

Cosine’s Special Values: A Memory Jogger

Now, let’s embark on a journey to discover the cosine values of special angles:

• 0°: The cosine of zero degrees is 1. This is because the terminal side of the angle lies on the positive x-axis, giving an x-coordinate of 1.
• 30°: The cosine of thirty degrees is √3 / 2. The terminal side forms a 30-60-90 triangle, where the adjacent side (x-coordinate) is √3 / 2.
• 45°: The cosine of forty-five degrees is √2 / 2. The terminal side bisects the first quadrant, forming a 45-45-90 triangle, where the x-coordinate is √2 / 2.
• 60°: The cosine of sixty degrees is 1 / 2. The terminal side forms a 30-60-90 triangle, where the adjacent side (x-coordinate) is 1 / 2.
• 90°: The cosine of ninety degrees is 0. The terminal side lies on the y-axis, resulting in an x-coordinate of 0.

Cosine of Complementary Angles: A Tale of Two Sides

Trigonometry is a fascinating world of angles and triangles, where the cosine function plays a pivotal role. One intriguing aspect of cosine is its relationship with complementary angles.

Complementary Angles: A Pair of Perfect Partners

Complementary angles are like two pieces of a puzzle that fit together perfectly. They are two angles whose sum equals 90 degrees. Imagine a right-angled triangle: the two acute angles are complementary.

Cosine’s Connection: A Special Bond

The cosine function is a measure of the ratio of the adjacent side to the hypotenuse in a right-angled triangle. When we consider complementary angles in a right-angled triangle, a beautiful pattern emerges.

Cosine of Complementary Angles: A Balanced Equation

• In a right-angled triangle, the cosine of an angle is equal to the sine of its complementary angle.

For example:
– If one acute angle in a right-angled triangle is 30 degrees, its cosine value is 0.5 (or 1/2).
– The complementary angle is 60 degrees, and its sine value is also 0.5.

This relationship arises from the Pythagorean identity, which states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. This identity allows us to find the value of one trigonometric function if we know the value of the other in the same right-angled triangle.

Proof of the Theorem

Consider a right-angled triangle with acute angles A and B, where A + B = 90 degrees.

• Let’s assume the hypotenuse is c, the adjacent side opposite angle A is a, and the adjacent side opposite angle B is b.

• Using the Pythagorean theorem, we can write:

a^2 + b^2 = c^2

• We can divide both sides by c^2 to get:

(a/c)^2 + (b/c)^2 = 1

• But a/c = cos(A) and b/c = sin(B). So we have:

cos(A)^2 + sin(B)^2 = 1

• Since A and B are complementary, cos(A) = sin(B). Therefore,

cos(A) = sin(B)

The Power of Complementarity

The cosine of complementary angles is a fundamental concept in trigonometry. It helps us solve complex problems and understand the relationships between angles in various applications, such as navigation, surveying, and engineering.

Next time you encounter a problem involving complementary angles and cosine, remember this special bond. It will guide you to the right solution with ease and efficiency.

Quadrantal Angles and Cosine: Unveiling the Secrets

In the realm of trigonometry, angles reign supreme, and quadrantal angles hold a special place. These are angles that measure exactly 0°, 90°, 180°, or 270°, and their cosine values are particularly noteworthy.

As we traverse the unit circle, imagine standing at the origin (0°). Moving counterclockwise, we encounter two key quadrantal angles:

• 90°: Also known as the right angle, this angle forms a right triangle with the horizontal axis. The cosine of 90° is 0, as the adjacent side to the angle is zero.

• 180°: This is the straight angle, which creates a line parallel to the horizontal axis. Its cosine is also -1, since the adjacent side lies to the left.

Venturing into the other quadrants, we encounter two more quadrantal angles:

• 270°: This angle is perpendicular to the vertical axis. The cosine of 270° is 0, mirroring its value at 90°.

• 360° (or 0°): This is a full rotation, completing the circle. Its cosine is 1, as it brings us back to the starting point.

Keep these values in mind, as they form the foundation for understanding cosine in all scenarios. Remember, the beauty of trigonometry lies in its ability to describe the relationship between angles and sides in triangles, making it an indispensable tool in science, engineering, and countless other fields.

The Graph of the Cosine Function: A Visual Representation of Periodic Oscillation

The cosine function, a cornerstone of trigonometry, is a mathematical marvel whose graph captures the essence of periodic oscillation. Its sinusoidal curve dances across the coordinate plane, tracing the rhythmic rise and fall of countless phenomena in our universe.

The graph of the cosine function, a smooth and continuous curve, resembles the shape of a wave. It oscillates between a maximum value of 1 and a minimum value of -1. The wavelength—the horizontal distance between consecutive peaks or troughs—represents the period of the oscillation. The amplitude, or half the distance between the crest and trough, reflects the intensity of the oscillation.

Key Characteristics of the Cosine Function Graph:

• Symmetrical about the y-axis: The graph mirrors itself across the vertical axis.
• Periodic: The pattern repeats itself over equal intervals along the x-axis.
• Intercepts: The graph crosses the x-axis at regular intervals, known as the zeros of the function.
• Extrema: The peaks and troughs of the graph represent the maximum and minimum values of the function.
• Asymptotes: The graph approaches, but never touches, the horizontal lines y = 1 and y = -1.

The Inverse Cosine Function: Unveiling the Arcsine’s Secrets

In the realm of trigonometry, where sine and cosine dance together, the inverse cosine function (arcosine) emerges as a pivotal player. It’s the key to unlocking the hidden angles that lie behind cosine values.

Imagine yourself at a masquerade ball, where everyone wears masks. The cosine function is the masked figure, concealing the true angle beneath its cloak. The arcosine function, however, is the unmasking agent, revealing the angle’s identity.

To grasp the arcosine, let’s consider the range of cosine values. Cosine, like a chameleon, takes on values between -1 and 1, depending on the angle it represents. When cosine wears the disguise of -1, the angle is 180 degrees; when it’s 0, the angle is 90 degrees.

The arcosine function is the inverse of cosine, just as the inverse of a lock is a key. It takes a cosine value and reveals the angle that produced it. Arcosine, like a secret codebreaker, uncovers the hidden angle from the cosine’s mask.

Properties of the Arcosine Function:

• Range: 0° to 180°
• Inverse: cosine
• Domain: -1 to 1

Notation:

The arcosine function is commonly denoted as:

• arccos(x)

where x is the cosine value.

Example:

To find the angle whose cosine is 1/2, we use the arcosine function:

arccos(1/2) = 60°

This means that the angle that produces a cosine value of 1/2 is 60 degrees.

Applications:

The arcosine function finds widespread applications in various fields, including:

• Navigation
• Signal processing
• Computer graphics
• Astronomy

By understanding the inverse cosine function, you gain a deeper insight into trigonometry and its practical uses. So, embrace the arcosine function as the key that unveils the hidden angles and empowers you to navigate the complexities of the trigonometric realm.