Circumscribing A Circle Around A Triangle: A Comprehensive Guide

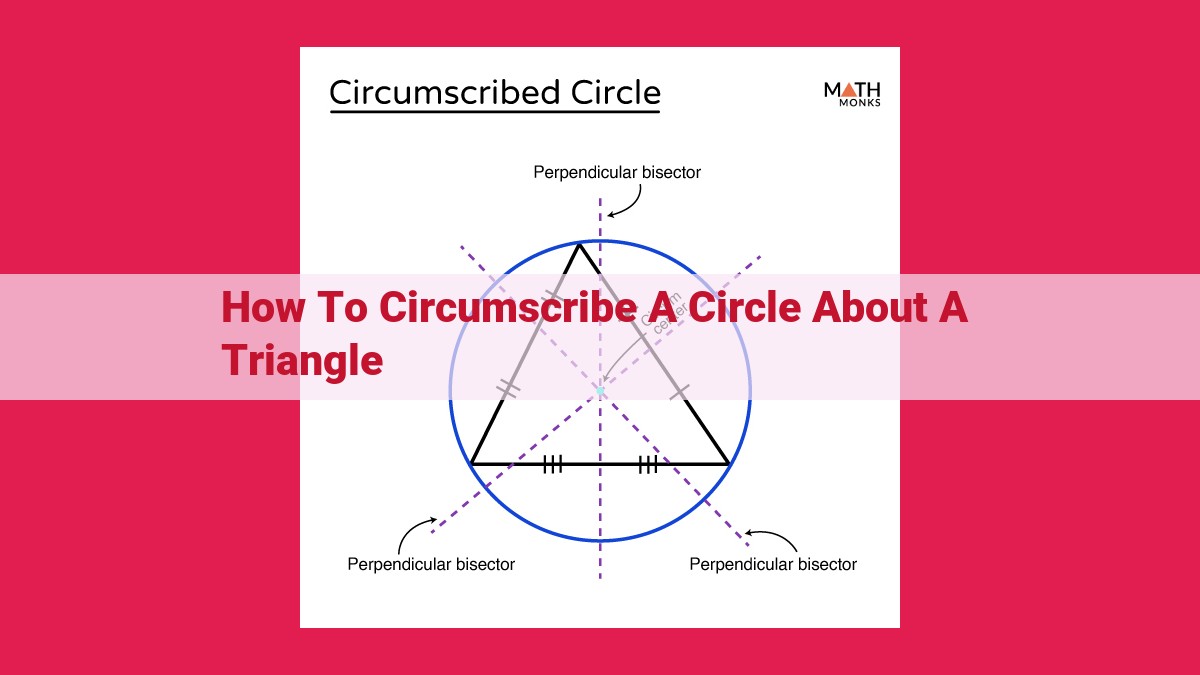
To circumscribe a circle about a triangle, find the circumcenter, the intersection of the perpendicular bisectors of the triangle’s sides. The circumradius, the distance from the circumcenter to any vertex, defines the circle’s radius. This process involves identifying triangle properties such as angle bisectors, perpendicular bisectors, and side lengths, and applying formulas like Heron’s Formula and the Law of Cosines. The circumscribed circle provides insights into the triangle’s geometry and has applications in fields like architecture and surveying.

Circumscribed Circles: A Geometric Gateway to Understanding Triangles

Imagine a circle that perfectly fits around a triangle, kissing each of its vertices like a gentle embrace. This enchanting circle is known as the circumscribed circle, and it holds a treasure trove of geometric secrets within its boundary.

Key Properties of a Circumscribed Circle:

• It passes through all three vertices of the triangle.
• It has the same radius, known as the circumradius, from its center to any of the vertices.
• The circumcenter, the center point of the circumscribed circle, is the intersection point of the perpendicular bisectors of the triangle’s sides. These bisectors are lines that cut each side in half and are perpendicular to it.

The Circumcenter: Where Perpendicular Bisectors Meet

In the realm of geometry, the circumcenter holds a pivotal position in understanding the intricate relationships between the sides and angles of a triangle. It emerges as the point where three perpendicular bisectors intersect, each bisecting a different side of the triangle.

The circumcenter, often denoted by the letter ‘O,’ is not merely a geometric curiosity but a point of strategic importance. Its significance lies in its ability to connect the triangle’s vertices to a circumscribed circle, a circle that gracefully passes through all three points. This circle’s radius, known as the circumradius, plays a crucial role in determining the triangle’s properties and forming a circle around it.

The perpendicular bisectors, the guiding lights leading to the circumcenter, are perpendicular lines that intersect a side of a triangle at its midpoint. These bisectors, adorned with the power of perpendicularity, divide the side into two congruent parts, ensuring that the distances from the bisector to the vertices are equal. Their intersection at the circumcenter creates an equilibrium, a perfect balance of distances from all three vertices.

The circumcenter, like a wise sage, governs the triangle’s intricacies. It orchestrates a harmonious dance between the angle bisectors, perpendicular bisectors, and the circumradius, forming a web of interconnected properties that define the triangle’s geometric identity. It serves as a compass, guiding the exploration of a triangle’s secrets, revealing its hidden truths.

**Exploring the Circumradius: A Key Measure in Triangle Geometry**

In the realm of geometry, the study of triangles often involves understanding their relationship with circles that touch or enclose them. One such circle is the circumscribed circle, which elegantly passes through all three vertices of a triangle. At its heart lies a pivotal concept known as the circumradius, a measure that unveils crucial insights into the triangle’s properties.

Imagine a circle meticulously drawn around a triangle, its circumference perfectly enveloping the three corners. The circumradius is the distance from the circumcenter (the circle’s center) to any one of the triangle’s vertices. This value represents the radius of the circumscribed circle and holds a profound connection with the triangle’s geometry.

The circumcenter, an enigmatic point within the triangle, is where the perpendicular bisectors of its three sides intersect. It serves as the equidistant point, lying at an equal distance from all three vertices. This equidistant property governs the circumradius, making it a crucial parameter for analyzing the triangle’s shape and dimensions.

Triangle Properties Relevant to Circumscribed Circles

Every triangle has a circumscribed circle that passes through all three of its vertices. This circle provides valuable insights into the triangle’s properties and relationships. Let’s explore some key triangle properties related to circumscribed circles:

• Angle Bisectors: The angle bisectors of a triangle intersect at the circumcenter, which is the center of the circumscribed circle. This point is equidistant from all three vertices, making it a crucial point for triangle analysis.

• Perpendicular Bisectors: The perpendicular bisectors of a triangle’s sides also intersect at the circumcenter. These lines are perpendicular to each side and bisect them, providing additional insights into the triangle’s geometry.

• Medians: Medians are line segments connecting a vertex to the midpoint of the opposite side. In a triangle with a circumscribed circle, the circumcenter lies on the intersection of the three medians, known as the centroid.

• Side Lengths: The circumscribed circle’s circumradius (the distance from the circumcenter to any vertex) is closely related to the triangle’s side lengths. Various formulas, such as Heron’s Formula and the Law of Cosines, can be used to calculate the circumradius based on the side lengths.

• Various Formulas: Several formulas play a significant role in understanding triangles with circumscribed circles. These include Heron’s Formula, the Law of Cosines, the Law of Sines, Ptolemy’s Theorem, and Euler’s Formula. These formulas provide valuable tools for studying triangle properties, including those related to circumscribed circles.

Circumcribing a Circle about a Triangle: A Step-by-Step Guide

In the realm of geometry, a circumscribed circle is a special type of circle that shares a harmonious relationship with triangles. It’s a circle that nestles snugly around a triangle, with each of the triangle’s three vertices kissing its perimeter.

This article will take you on a delightful journey, guiding you through the steps of circumscribing a circle about a triangle. Along the way, you’ll uncover the secrets of the circumcenter, the enigmatic point where perpendicular bisectors intersect. You’ll also meet the circumradius, the circle’s loyal companion that keeps it at a constant distance from each vertex.

Step 1: Gather Your Tools

Before embarking on this geometric escapade, you’ll need a few trusty tools: a compass, a straightedge, and a keen eye for precision. Armed with these instruments, you’re ready to conquer the triangle world!

Step 2: Find the Circumcenter

The circumcenter is the magical point where the perpendicular bisectors of all three sides of the triangle intersect. To find it, follow these steps:

• Draw the perpendicular bisector of any side.
• Repeat for the other two sides.
• The point where all three perpendicular bisectors meet is the circumcenter.

Step 3: Determine the Circumradius

Once you have the circumcenter, finding the circumradius is a breeze. The circumradius is simply the distance from the circumcenter to any vertex of the triangle. Using your compass, measure this distance.

Step 4: Draw the Circumscribed Circle

With the circumcenter and circumradius in your grasp, you’re ready to draw the circumscribed circle. Place the compass point on the circumcenter and extend it to the circumradius. Swing the compass around the circumcenter, and voila! You’ve successfully circumscribed a circle about the triangle.

Understanding how to circumscribe a circle about a triangle is a fundamental skill in geometry. It helps you comprehend triangle properties, solve geometric problems, and appreciate the beauty of geometry’s intricate relationships. So, next time you encounter a triangle, remember these steps and become a master of circumscribed circles!