Calibration Curves: Essential Tool For Accurate Sample Concentration Measurement
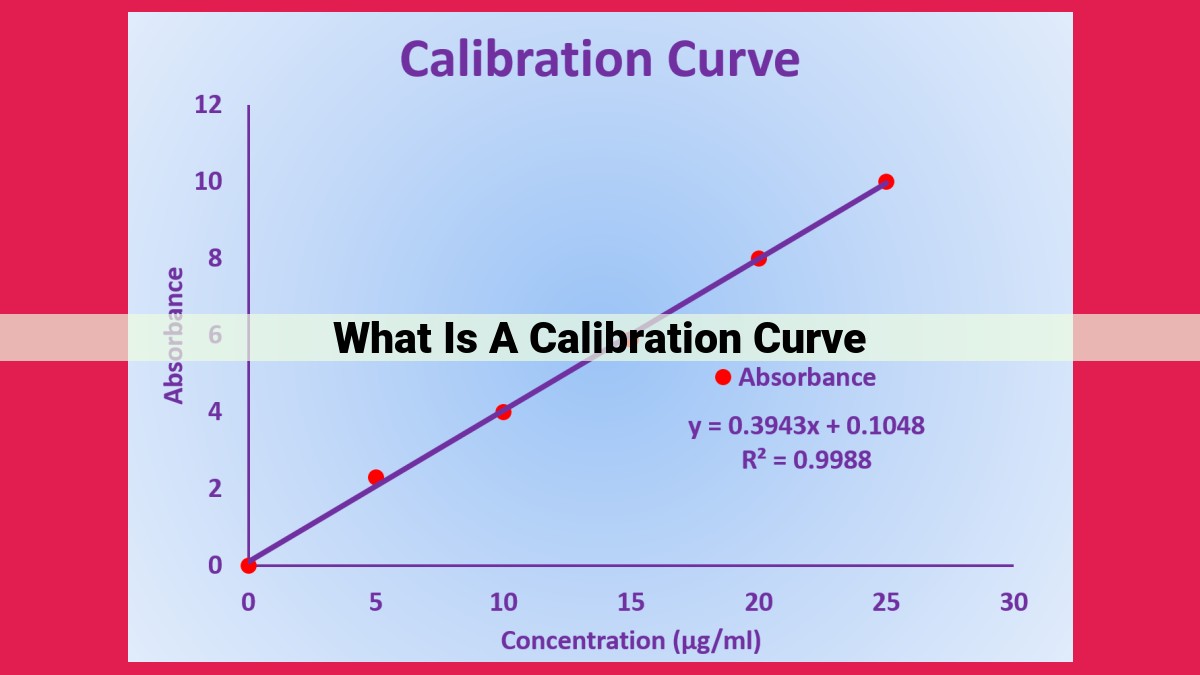
A calibration curve establishes a relationship between known sample concentrations (standards) and their corresponding instrument responses (calibration points). It’s a graphical representation that enables the quantification of unknown samples. The linearity, slope, and intercept of the curve are crucial in determining method performance, including sensitivity and accuracy. Calibration curves are essential in analytical chemistry, used in techniques like spectroscopy, chromatography, and electrochemistry, to ensure reliable and reproducible results. They enable the accurate measurement of sample concentrations by comparing unknown responses to the calibrated curve.
Understanding Calibration Curves: A Foundation for Analytical Chemistry
In the realm of analytical chemistry, calibration curves stand as essential tools for ensuring the accuracy and reliability of our results. But what exactly are calibration curves, and how do they work? Let’s delve into the basics:
Definition and Purpose
A calibration curve is a graphical representation of the relationship between the concentration of a known analyte and the corresponding instrument response. By establishing this relationship, we can quantify unknown analyte concentrations in future samples.
Key Components
Building a calibration curve involves several critical components:
- Standards: A series of solutions with known analyte concentrations.
- Calibration Points: The specific concentrations at which data points are collected.
- Linearity: The degree to which the relationship between concentration and response is a straight line.
- Slope: The steepness of the calibration curve, indicating the sensitivity of the method.
- Intercept: The value on the y-axis where the calibration curve intersects, representing the instrument response when no analyte is present.
Calibration Curve Principles
In analytical chemistry, calibration curves play a pivotal role in ensuring the accuracy and reliability of your results. These curves establish a fundamental relationship between the concentration of an analyte in a sample and the corresponding instrument response. Understanding the principles behind calibration curves is crucial for extracting meaningful data and making informed decisions.
Linearity and Sensitivity
A linear calibration curve is characterized by a straight line that passes through the origin or zero concentration. This linearity is essential for accurate quantification. The sensitivity of the method, represented by the slope of the line, indicates the magnitude of the instrument response for a given change in analyte concentration. A steeper slope indicates higher sensitivity, allowing for better discrimination between samples with different concentrations.
Role of Slope and Intercept
The slope of the calibration curve provides valuable information about the method performance. It represents the change in instrument response per unit change in analyte concentration. A non-zero intercept indicates the presence of a background signal. This background signal can arise from various sources, such as instrument noise or impurities in the reagents. It is essential to account for the intercept to minimize errors in sample quantification.
By understanding the importance of linearity, sensitivity, slope, and intercept, you can not only establish reliable calibration curves but also assess the accuracy and precision of your analytical method. This knowledge empowers you to make informed decisions and interpret your experimental data with confidence.
Applications of Calibration Curves: Unlocking Accurate Quantification
In the realm of analytical chemistry, calibration curves serve as indispensable tools for enabling precise quantification of unknown samples. These curves provide a fundamental understanding of the relationship between the response of an analytical instrument and the concentration of the analyte of interest.
One of the most common analytical techniques that heavily relies on calibration curves is spectrophotometry. In spectrophotometry, the absorbance of a sample at a specific wavelength is measured and correlated to its concentration. By creating a calibration curve using known standards, analysts can determine the concentration of an unknown sample based on its absorbance.
Another important application of calibration curves is in chromatography. Techniques such as high-performance liquid chromatography (HPLC) and gas chromatography (GC) separate and identify compounds based on their interactions with a stationary phase. By injecting known standards and plotting the retention time or peak area against concentration, a calibration curve can be established. This curve allows for the quantification of unknown compounds in a sample by comparing their retention times or peak areas to the calibration curve.
How Calibration Curves Facilitate Accurate Quantification
The accuracy of quantification using calibration curves hinges upon several key factors. Firstly, the linearity of the calibration curve is crucial. A linear relationship ensures that the response of the instrument is directly proportional to the concentration of the analyte, making it possible to interpolate or extrapolate the concentration of unknown samples.
Secondly, the sensitivity of the analytical method is essential. A sensitive method will produce a significant response for small changes in analyte concentration, resulting in more precise quantification. Sensitivity is often reflected in the slope of the calibration curve, with a steeper slope indicating higher sensitivity.
By utilizing calibration curves, analysts can confidently quantify unknown samples and attain reliable and reproducible results. These curves empower scientists to make informed decisions, advance research, and ensure the accuracy of analytical data in various fields.
Benefits of Using Calibration Curves
Calibration curves are invaluable tools in analytical chemistry, providing numerous benefits for accurate and reliable data analysis.
Accurate Quantification of Unknown Samples
Calibration curves enable the precise determination of the concentration of unknown samples. By comparing the response of an unknown sample to that of a series of known standards, the concentration of the analyte in the sample can be calculated. This process requires a linear relationship between the response and concentration, ensuring the accuracy of the quantification.
Assessment of Method Linearity and Sensitivity
Calibration curves also provide insights into the linearity and sensitivity of the analytical method. The slope of the curve represents the sensitivity, indicating the change in response for a unit change in concentration. A steeper slope implies higher sensitivity, while a flatter slope indicates lower sensitivity. The linearity of the curve reflects how well the data points fit a straight line, allowing for reliable extrapolations within the linear range.
Determination of Detection and Quantification Limits
Calibration curves help establish the detection limit and quantification limit of the analytical method. The detection limit is the lowest concentration that can be reliably detected, while the quantification limit is the lowest concentration that can be accurately measured. These limits define the sensitivity of the method and help determine its suitability for a specific application.
In summary, calibration curves are essential for:
- Precisely quantifying unknown samples
- Evaluating the linearity and sensitivity of analytical methods
- Establishing detection and quantification limits
Their widespread use in analytical chemistry ensures reliable and reproducible results, making them indispensable tools for accurate data interpretation.
Importance of Calibration Curves in Analytical Chemistry
Calibration curves play a pivotal role in analytical chemistry, ensuring the reliability, reproducibility, and accuracy of analytical results. They act as the foundation for accurate quantification of unknown samples, facilitating the determination of specific analytes in various matrices. Let’s delve into their significance:
Ensuring Reliable and Reproducible Results
Calibration curves establish a direct relationship between the concentration of an analyte and the corresponding analytical signal, whether it be absorbance, fluorescence, or any other measurable parameter. By plotting known concentrations of the analyte against the instrument’s response, these curves provide a reference against which unknown samples can be compared. This comparison allows for the accurate determination of analyte concentrations in real-world samples, promoting confidence in the analysis.
Compensation for Matrix Effects and Improved Data Accuracy
Real-world samples often contain a complex mixture of components that can interfere with the analytical signal of the target analyte. These matrix effects can lead to inaccuracies or false readings, hindering reliable quantification. Calibration curves can compensate for these interferences by incorporating matrix-matched standards into the calibration process. By matching the calibration standards to the unknown sample matrix, the influence of matrix effects is minimized, resulting in more accurate and reliable data.