Calculating Solid Volumes: Methods And Applications

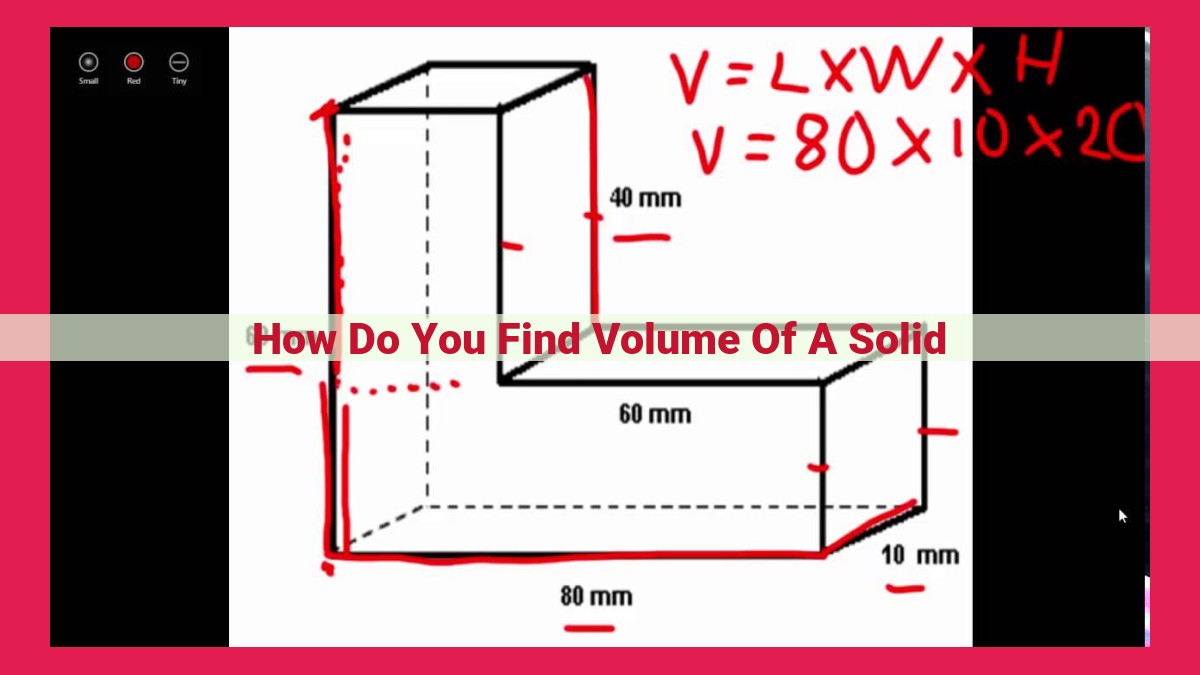
To find the volume of a solid, various methods are employed based on its shape and properties. For regular solids like Platonic, Archimedean, and Johnson solids, their known formulas can be applied. Cavalieri’s Principle establishes the relationship between volumes of solids and planar cross-sections, enabling volume calculations. The Method of Exhaustion and integration methods are more general, utilizing limits and integrals to determine volume. Techniques like the Shell Method and Disk Method involve dividing a solid into cross-sectional areas, using integrals to compute their volumes. These methods provide powerful tools for calculating volumes of complex solids and are widely used in mathematics and engineering.

Unveiling the Secrets of Volume Calculation for 3D Solids

In our three-dimensional world, understanding the volume of objects is crucial for a wide range of applications. From architects designing buildings to engineers constructing bridges, calculating the volume of solids is an essential skill. In this article, we will embark on a journey to explore the key concepts and techniques used to determine the volume of various three-dimensional shapes, making complex mathematical ideas accessible and engaging.

Essential Concepts and Techniques

To delve into the realm of volume calculation, we must first establish the fundamental concepts and techniques that pave the way for understanding. These include:

• Cavalieri’s Principle: A groundbreaking idea that establishes a relationship between the volumes of solids with equal cross-sectional areas.
• Method of Exhaustion: An ancient yet powerful approach that approximates volumes using an infinite series of shapes.
• Integration: A mathematical tool that allows us to find the area under curves and, in turn, the volume of solids.
• Cross-sectional Area: The area of a plane that intersects a three-dimensional solid, crucial for volume calculations using methods such as the shell method and disk method.
• Volume of Revolution: The volume of a solid generated by rotating a two-dimensional region around an axis.

Practical Applications

Equipped with these fundamental concepts, we can now delve into the practical applications of volume calculation:

• Shell Method: Approximates the volume of a solid by dividing it into cylindrical shells, each with a radius and height.
• Disk Method: Approximates the volume of a solid by stacking circular disks with varying radii.
• Washer Method: A variation of the disk method used for solids with holes.

Discovering the Fascinating World of Regular Solids

In the realm of three-dimensional geometry, regular solids hold a captivating allure, enticing mathematicians and artists alike for centuries. These enigmatic shapes, boasting identical faces and edges, have played a profound role in human understanding of the physical world.

Platonic Solids: The Pillars of Geometry

At the pinnacle of regular solids stand the Platonic solids, named after the ancient Greek philosopher Plato. These five perfect forms—the tetrahedron, cube, octahedron, dodecahedron, and icosahedron—possess not only identical faces and edges but also congruent faces. These solids have captivated minds for millennia, inspiring awe in their symmetry and simplicity.

Archimedean Solids: Regular Faces and Identical Vertices

Just below the Platonic solids in terms of symmetry are the Archimedean solids. These 13 solids also boast identical faces, but their vertices are all equivalent rather than congruent. As a result, Archimedean solids display a unique blend of symmetry and complexity, capturing the imagination with their intricate patterns.

Johnson Solids: Regular Faces but Not Platonic or Archimedean

In the realm of irregular but still remarkable solids, we find the Johnson solids. These 92 shapes have identical faces but do not meet the strict criteria of Platonic or Archimedean solids. Their unique properties have made them subjects of fascination for mathematicians who appreciate their beauty and complexity.

From the awe-inspiring Platonic solids to the intriguing Johnson solids, the world of regular solids is a testament to the wonders of geometry. These shapes continue to captivate our minds, fostering our understanding of the physical world and inspiring generations of mathematicians, artists, and enthusiasts alike.

Cavalieri’s Principle: Unlocking the Secrets of Three-Dimensional Volumes

In the realm of mathematics, calculating the volume of three-dimensional solids plays a crucial role in understanding the shape and size of our physical world. Among the many techniques used, Cavalieri’s Principle stands out as an elegant and foundational concept that offers a powerful tool for unraveling these volumes.

Cavalieri’s Principle states that if two solids have the same height and cross-sectional areas at every level parallel to their bases, then they have the same volume. This principle provides a geometric interpretation of volume that allows us to visualize and compare the volumes of different solids.

For example, consider two solids, one in the shape of a cube and the other in the shape of a pyramid. Both solids have the same height. By slicing both solids horizontally at various levels, we can observe that they have the same cross-sectional areas at each level. According to Cavalieri’s Principle, this implies that the two solids have the same volume, even though their shapes appear to be different.

Cavalieri’s Principle for Planes is a special case of this principle that applies to two-dimensional figures. It states that if two figures lying between two parallel lines have the same area at every height, then they have the same total area. This principle is particularly useful in finding the area of irregular figures, as it allows us to subdivide the figure into horizontal slices and calculate the area of each slice.

By understanding and applying Cavalieri’s Principle, we gain a deeper comprehension of three-dimensional shapes and their volumes. This principle continues to serve as a cornerstone in modern mathematics, paving the way for countless applications in physics, engineering, and beyond.

The Method of Exhaustion: A Journey Through the History of Volume Calculation

In the realm of mathematics, unraveling the mysteries of volume has played a pivotal role for centuries. The Method of Exhaustion, a venerable concept, has guided us towards a deeper understanding of the intricacies hidden within three-dimensional forms.

Imagine being an ancient mathematician, confronted with the challenge of measuring the volume of a sphere. How could you possibly determine the exact amount of space it occupied? The Method of Exhaustion, attributed to the Greek mathematician Eudoxus, provided a brilliant solution.

The method involves a meticulous sequence of approximations. By progressively dividing the sphere into smaller and smaller polygonal pieces, you’d create a series of figures that increasingly resembled the original sphere. With each iteration, the volume of these figures would become closer and closer to the true volume of the sphere.

The Method of Exhaustion, through its elegance and power, transcended its ancient origins. It found renewed relevance in modern calculus, where it underpins the concepts of Riemann integrals and definite integrals. These integrals allow us to precisely calculate areas and volumes under curves, unlocking insights into a vast array of mathematical problems.

The legacy of the Method of Exhaustion is undeniable. It has been an indispensable tool in the evolution of volume calculation, contributing significantly to our understanding of the three-dimensional world. As we continue to explore the depths of mathematics, the Method of Exhaustion serves as a timeless testament to the enduring power of human ingenuity.

Integration

• Using integration to find the area under a curve and volume of a solid
• Indefinite and definite integrals

Integration: Unlocking the Secrets of Volumes and Curves

In our exploration of three-dimensional solids, integration reigns supreme as a powerful tool for unlocking the mysteries of their volumes and the areas beneath their curves. It’s like having a secret key that opens doors to a vast world of shapes and mathematical beauty.

Integration, in essence, is a method of adding up infinitesimally small pieces to find the total area or volume of an object. It’s like slicing a solid into thin layers and then stacking them up to get its full height. Or, it’s like calculating the total area under a curve by dividing it into tiny rectangles and adding up their areas.

At its core, integration is built on two fundamental concepts: indefinite integrals and definite integrals. Indefinite integrals represent the antiderivative of a function, a function that has the original function as its derivative. They provide us with a general expression for the area under a curve.

Definite integrals, on the other hand, calculate the exact area under a curve over a specific interval. They allow us to determine the volume of a solid generated by rotating a region around a line or axis.

Understanding and applying integration is not just about technical formulas and calculations. It’s about unlocking a deeper appreciation for the intricate shapes that surround us and gaining a profound understanding of the relationship between curves and solids. From calculating the volume of a sphere to finding the area under a complex function, integration empowers us to unravel the secrets of our mathematical universe.

Cross-Sectional Area: The Foundation for Shell and Disk Methods

In the quest to unravel the enigmatic world of three-dimensional solids, cross-sectional area emerges as a beacon of clarity. It’s the area of a slice taken perpendicular to the solid’s length, like a cross-section of a loaf of bread.

Understanding cross-sectional area is paramount in unlocking the secrets of two formidable mathematical tools: the Shell Method and the Disk Method. These techniques make calculating the volume of solids a breeze.

Shell Method and Disk Method

Imagine slicing the solid into cylindrical shells or circular disks. The Shell Method views the solid as a tapestry of thin cylindrical shells, stacked side by side. By meticulously summing up the volume of each shell, we can unravel the solid’s overall volume.

Similarly, the Disk Method envisions the solid as a meticulous arrangement of circular disks, piled upon each other. By painstakingly calculating the volume of each disk, we can piece together the total volume.

Applications in Real-World Scenarios

Cross-sectional area isn’t just a mathematical abstraction; it’s a potent tool with real-world applications. For instance, it’s used in engineering to determine the volume of architectural structures and estimate the capacity of storage tanks. In medicine, it aids in calculating the volume of organs for diagnostic purposes.

Cross-sectional area may seem like a minor player in the realm of solid geometry, but its importance cannot be overstated. As the cornerstone of the Shell and Disk Methods, it empowers us to conquer the complexities of volume calculations and uncover the hidden dimensions of our three-dimensional world.

Unveiling the Secrets of Volume Calculation: A Comprehensive Guide

Calculating the volume of three-dimensional solids is crucial in various fields, from engineering to architecture. This blog post will delve into essential concepts and techniques to empower you with the knowledge to master this fundamental mathematical skill.

Regular Solids

Regular solids, such as cubes, pyramids, and dodecahedrons, possess unique characteristics. Platonic solids have identical faces and edges, while Archimedean solids boast regular faces and identical vertices. Johnson solids, on the other hand, have regular faces but are not fully regular or Archimedean.

Cavalieri’s Principle

Cavalieri’s Principle states that if two solids have equal cross-sectional areas at every level, then they have equal volumes. This principle is particularly useful for calculating the volume of solids with irregular shapes.

Method of Exhaustion

The Method of Exhaustion, an ancient technique, involves dividing a given solid into an infinite number of smaller solids. By finding the volume of each smaller solid and summing them up, we can approximate the volume of the original solid.

Integration

Integration, a more modern approach, allows us to find the area under a curve, which can be used to calculate the volume of a solid. We can use both indefinite and definite integrals for this purpose.

Cross-sectional Area

The cross-sectional area of a solid represents the area of a slice at a specific point along its length or width. This concept is pivotal in calculating the volume using methods like the shell method and disk method.

Volume of Revolution

The Volume of Revolution refers to the volume of a solid generated when a two-dimensional figure is rotated around an axis. Common Solids of Revolution include spheres, cones, and cylinders. By slicing and integrating these solids, we can determine their volumes precisely. Among the key methods for calculating Volume of Revolution are:

Shell Method

• The shell method involves dividing the solid into cylindrical shells of equal thickness.
• The volume of each shell is calculated by multiplying the cross-sectional area at its midpoint by the circumference of the shell.
• The total volume is obtained by adding up the volumes of all the shells.

Disk Method

• The disk method divides the solid into circular disks of equal thickness.
• Each disk’s volume is determined by multiplying the disk’s area by its thickness.
• The total volume is calculated by integrating the disk volumes over the range of the solid’s height.
• The washer method is a variation of the disk method used for solids with holes.

The Shell Method: Unraveling Solid Volumes

Imagine a cylindrical shell, a thin layer of a solid with a hollow interior. The Shell Method is a powerful calculus technique that allows us to calculate the volume of solids by stacking up an infinite number of these cylindrical shells.

Concept:

The Shell Method relies on the idea that a solid can be approximated as a collection of cylindrical shells. Each shell has a radius r, a height h, and a very small thickness Δr. The volume ΔV of each shell is calculated using the formula:

ΔV = 2πr * h * Δr

Steps:

1. Integrate the Shell Formula: Integrate the formula for the volume of a shell over the appropriate range of r to find the total volume V of the solid.
2. Determine the Limits of Integration: The limits of integration will depend on the shape of the solid and the axis of rotation.
3. Evaluate the Integral: Calculate the definite integral to obtain the volume of the solid.

Applications:

The Shell Method is particularly useful for calculating the volume of solids that have a non-circular or irregular cross-section. Some common examples include:

• Solids of Revolution: Solids formed by rotating a two-dimensional region about an axis
• Solids with Holes: Solids with circular or non-circular holes or cavities

The Marvelous World of Volume Calculations: Unveiling the Secrets of 3D Solids

From the imposing pyramids of ancient Egypt to the sleek skyscrapers that define modern cities, the ability to calculate the volume of three-dimensional solids has played a pivotal role throughout history. In this intriguing exploration, we will delve into the intriguing world of volume calculations, unveiling the essential concepts and techniques that empower us to unlock the secrets of these fascinating shapes.

Regular Solids: Architectural Masterpieces of Geometry

Among the realm of three-dimensional solids, regular solids stand out as paragons of symmetry and elegance. These captivating shapes, such as Platonic, Archimedean, and Johnson solids, boast identical faces and vertices. Their geometric perfection has captivated mathematicians and artists alike for centuries.

Cavalieri’s Principle: The Rosetta Stone of Volume

The Cavalieri’s Principle, a cornerstone of volume calculations, provides a profound insight into the relationship between solids and planes. It asserts that if two solids have equal cross-sectional areas at every level parallel to a given plane, then they possess equal volumes.

Method of Exhaustion: A Journey to the Infinite

The method of exhaustion, a historical gem, paves the way for us to calculate volumes using limits. By inscribing and circumscribing polygonal shapes within a given solid and then taking the limit as the number of polygons increases, we can determine its precise volume. This concept forms the foundation of modern integral calculus.

Integration: The Calculus of Volume

Integration emerges as a powerful tool for volume calculations. By calculating the area under a curve, we can determine the volume of a solid of revolution. The techniques of integration, including indefinite and definite integrals, provide a systematic approach for solving complex volume problems.

Cross-sectional Area: The Key to Slicing and Dicing

The cross-sectional area of a solid is the area of the plane that intersects the solid perpendicular to its axis. This fundamental concept serves as the basis for calculating volumes using methods such as the shell method and the disk method.

Shell Method: Unraveling Solids Layer by Layer

The shell method, a versatile technique, allows us to calculate the volume of a solid by approximating it as a sequence of thin cylindrical shells. Summing the volumes of these shells results in the total volume of the solid.

Disk Method: A Stack of Circular Disks

The disk method, another effective approach, approximates a solid as a stack of circular disks. The areas of these disks are multiplied by their thicknesses and then integrated to yield the solid’s volume. A variation of this method, the washer method, is employed when the solid possesses a hole.

As we conclude our exploration, the marvels of volume calculations continue to astound. From the intricate symmetries of regular solids to the precise approximations of integration, the ability to determine the volume of three-dimensional shapes remains a vital tool in fields ranging from architecture and engineering to physics and beyond.