Calculating Momentum: Understanding Newton’s Laws And The Impulse-Momentum Theorem

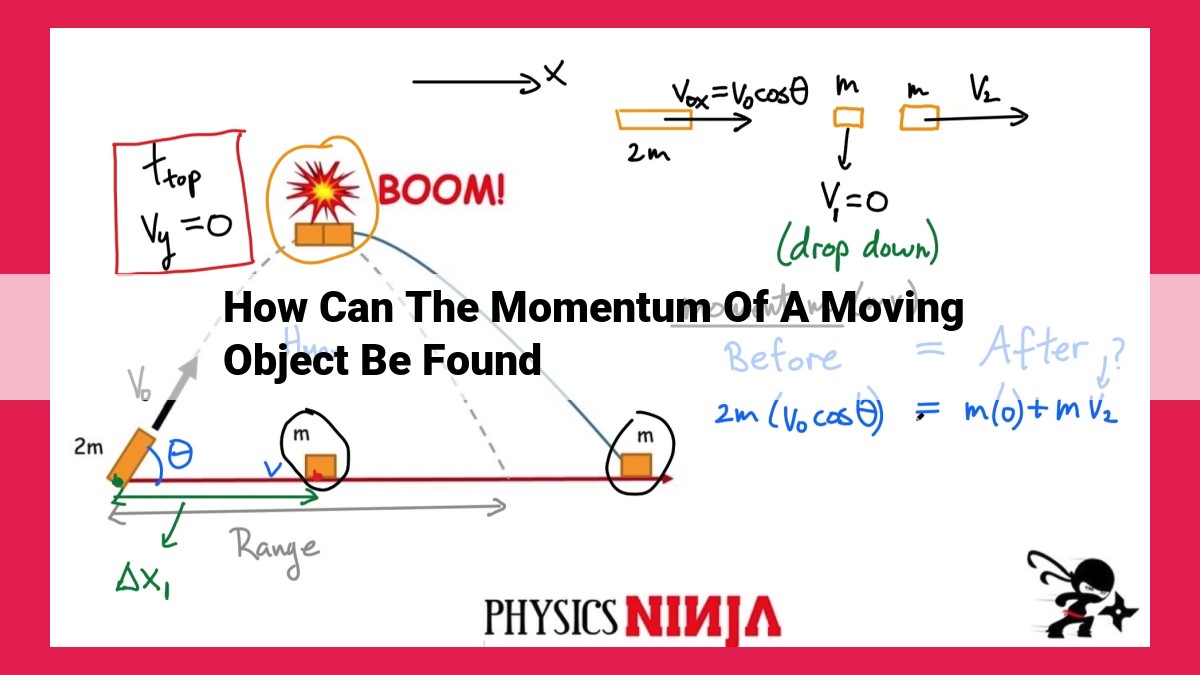
To determine the momentum of a moving object, Newton’s Second Law (F = ma) establishes the relationship between force, mass (m), and acceleration (a). Momentum (p) is a product of mass and velocity (v), and conservation of momentum states that total momentum remains constant in a closed system. The impulse-momentum theorem (J = Δp) measures the change in momentum (Δp) caused by an impulse (J), which equals the force applied over a time interval. By measuring the initial and final velocities of an object and applying these principles, the momentum can be calculated, considering the object’s mass, velocity, and time.

Newton’s Second Law of Motion:

• Explain the concept of force, mass, and acceleration.
• Introduce Newton’s second law and its mathematical expression.

Newton’s Second Law of Motion: Unraveling the Dynamic Trio of Force, Mass, and Acceleration

In the realm of physics, the interplay of force, mass, and acceleration profoundly shapes our understanding of motion. Enter the illustrious Newton’s Second Law of Motion, a cornerstone of classical mechanics that quantifies this intricate relationship.

Imagine a force as a gentle nudge or a forceful push. It’s the catalyst that causes matter to move. Mass, on the other hand, is the inherent property of an object that resists this motion. The greater the mass, the more “reluctant” it is to change its state.

Finally, we have acceleration, the rate at which an object’s velocity changes. It can be positive (speeding up) or negative (slowing down).

Now, let’s weave these concepts together in Newton’s Second Law: Force equals Mass multiplied by Acceleration. Written mathematically, it’s expressed as F = ma.

This law tells us that the force applied to an object is directly proportional to its mass and acceleration. In other words, a heftier object requires a greater force to accelerate, while a lighter object responds more readily to a given force.

Understanding Newton’s Second Law is not merely an academic pursuit. It’s a key tool for unlocking the secrets of the physical world. From the soaring of rockets to the mundane motion of everyday objects, this law underpins our comprehension of how forces shape our universe.

The Enigmatic Dance of Momentum: A Tale of Conservation

In the symphony of physics, the concept of momentum plays a central role. Momentum is the product of an object’s mass and velocity, representing its tendency to keep moving. Imagine a heavy boulder rolling down a hill; its momentum embodies the immense force behind its motion.

At the heart of momentum lies a fundamental principle: the Law of Conservation of Momentum. This law dictates that in a closed system, where no external forces act, the total momentum remains constant. It’s as if momentum is a precious treasure, carefully guarded within the system.

Consider a collision between two billiard balls. As the balls collide, momentum is exchanged between them. The momentum lost by the first ball is exactly equal to the momentum gained by the second. The total momentum of the system – the sum of the two balls’ momentum – remains unchanged.

This conservation principle has profound implications. It means that the momentum of an object can only be altered by introducing an external force. For instance, if you throw a baseball, the force of your arm imparts momentum to the ball. Once the ball leaves your hand, the only way to change its momentum is through air resistance or the impact of another object.

Understanding the Law of Conservation of Momentum provides invaluable insights into the workings of our world. It helps us predict the outcome of collisions, analyze the motion of celestial bodies, and design efficient transportation systems. It’s a principle that governs the smallest of particles to the grandest of cosmic events.

The Power of Impulse: Momentum Transformed

In the realm of physics, a force acting upon an object sets it into motion. This force may be applied for a brief period, or it may persist over an extended duration. Enter the realm of impulse-momentum, where the interplay between force, time, and the object’s inherent mass weaves a tapestry of motion.

Impulse: A Catalyst for Momentum

Impulse is, in essence, a force applied over a specific time interval. Just as momentum is the product of mass and velocity, impulse is the product of force and time. Like a spark that ignites a flame, impulse jolts an object from its state of rest or alters its momentum.

The Impulse-Momentum Theorem: A Universal Equation

In the realm of physics, the impulse-momentum theorem reigns supreme. It dictates that the total impulse acting on an object is equal to the change in its momentum. Mathematically expressed as (FΔt = Δp), this theorem provides the key to understanding how momentum transforms under the influence of force and time.

Exploring the Impulse-Momentum Theorem

Consider a soccer ball at rest. As a player strikes the ball, they exert a force upon it for a brief time interval. This impulse propels the ball into motion, imparting it with momentum. The greater the magnitude of the force or the duration of its application, the **greater the impulse and the resulting change in momentum_.

In a wider context, the impulse-momentum theorem finds myriad applications. From studying collisions and explosions to designing safety equipment and spacecraft propulsion systems, this fundamental principle illuminates the forces that govern the motion of all objects around us.

Change in Momentum: Calculating the Force of Interactions

In the realm of physics, momentum reigns supreme as a fundamental quantity that characterizes the motion of objects. Momentum is the product of an object’s mass and velocity, representing the amount of motion it possesses.

Imagine a soccer ball soaring through the air, carrying with it a substantial amount of momentum. As the ball strikes a sturdy wall, it undergoes a dramatic change in momentum. The wall exerts a force on the ball, causing its velocity to change abruptly.

This change in momentum is not merely a theoretical concept; it can be calculated using a simple formula:

Δp = p_f - p_i

where:

• Δp is the change in momentum
• p_f is the final momentum
• p_i is the initial momentum

To determine the change in momentum, we must first calculate the initial and final momentum of the object. This involves multiplying the object’s mass by its initial and final velocities.

For instance, if a 1.5-kilogram soccer ball has an initial velocity of 10 meters per second and a final velocity of 5 meters per second, the change in momentum is calculated as follows:

Δp = p_f - p_i
= (1.5 kg × 5 m/s) - (1.5 kg × 10 m/s)
= -7.5 kg m/s

The negative sign indicates that the ball’s momentum has decreased, which aligns with our observation that the ball slowed down after hitting the wall.

Understanding the change in momentum is crucial in various scenarios, including:

• Collisions: Calculating the change in momentum of colliding objects provides insights into the force and energy involved during the interaction.
• Rocket propulsion: The principle of change in momentum explains how rockets propel themselves by expelling exhaust at high speed, resulting in a change in momentum and generating thrust.
• Everyday experiences: From kicking a足球 to throwing a dart, the concept of change in momentum governs the forces and motions we encounter daily.

By grasping the concept of change in momentum, we gain a deeper appreciation for the fundamental principles that shape the physical world around us.

Newton’s Laws of Motion and Momentum: A Deeper Dive

Mass: The Key Determinant of Momentum

In the realm of physics, understanding the concept of momentum is crucial for unraveling the dynamics of objects in motion. Momentum is a fundamental quantity that measures the resistance of an object to a change in its motion. It is directly proportional to both mass and velocity.

Mass is a measure of the amount of matter in an object. It is an intrinsic property, meaning it remains constant regardless of an object’s motion. A more massive object has more momentum than a less massive object with the same velocity.

Consider two objects with the same velocity: a bowling ball and a tennis ball. The bowling ball, with its greater mass, possesses significantly more momentum than the tennis ball. This difference becomes evident when you try to stop their motion. The bowling ball’s greater momentum makes it much harder to bring it to a halt.

In the world of sports, for instance, the mass of an athlete plays a critical role in determining their momentum. A heavier player in a football game, for example, carries more momentum than a lighter player running at the same speed. This added momentum gives them an advantage in collisions, enabling them to power through tackles and push opponents out of the way.

Understanding the concept of mass is essential for comprehending the behavior of moving objects. It is a pivotal factor in determining momentum, which is a fundamental concept in physics and plays a vital role in numerous real-world applications, from predicting the outcomes of sports events to designing spacecraft and developing crash-resistant vehicles.

Velocity:

• Define velocity and explain how it relates to displacement and time.

Understanding the Concept of Velocity

In the realm of physics, velocity plays a pivotal role in describing the motion of objects. It is a vector quantity that measures the rate of change in an object’s position over time. Unlike speed, which only measures the magnitude of an object’s motion, velocity also considers its direction.

Velocity can be calculated by taking the ratio of an object’s displacement, which is the change in its position, to the time it takes to make that change. Mathematically, velocity is expressed as:

Velocity = Displacement / Time

Displacement and Time: The Building Blocks of Velocity

Displacement, measured in meters, represents the straight-line distance between an object’s initial and final positions. It is important to note that displacement is not the same as distance traveled, which may include curves and detours along the object’s path.

Time, measured in seconds, is the duration of an event or the interval between two points in time. In the context of velocity, it represents the amount of time it takes for an object to undergo a particular displacement.

The Significance of Velocity in Physics

Velocity is a fundamental concept in physics, as it helps us understand and predict the motion of objects. It allows us to determine the speed and direction of a moving body and calculate the force acting on it. Furthermore, velocity is essential for understanding concepts such as momentum, kinetic energy, and acceleration.

In everyday life, we encounter countless examples of velocity. From the speed at which a car travels to the velocity of a falling object, velocity plays a vital role in our understanding of the physical world around us.

Time:

• Discuss the role of time in calculating velocities and momentum changes.

Newton’s Laws of Motion and Momentum: A Beginner’s Guide

Imagine yourself in a car, driving along a highway at a constant speed. Suddenly, another car rear-ends your vehicle at high speed. What happens? According to Newton’s second law of motion, the impact results in acceleration, which is a change in velocity over time. The force of the crash is equal to the mass of your car multiplied by its acceleration.

Conservation of Momentum

Now, let’s consider a different scenario. Two objects, A and B, are moving in opposite directions with equal speeds. If they collide with each other, they will bounce off with the same relative speeds but in reversed directions. This is known as the law of conservation of momentum. Momentum is a measure of an object’s mass and velocity.

Impulse-Momentum Theorem

The impulse-momentum theorem states that the change in an object’s momentum is equal to the impulse applied to the object. Impulse is the force acting on an object over a period of time. It can be positive or negative, depending on the direction of the force.

Change in Momentum

The change in momentum of an object can be calculated by multiplying its mass by its change in velocity. If the object’s velocity increases, its momentum will also increase. Conversely, if the object’s velocity decreases, its momentum will decrease.

Role of Time

Time plays a crucial role in calculating velocities and momentum changes. Velocity is the displacement of an object over time. Therefore, knowing the initial and final positions of an object and the time it takes to move from one position to another, we can calculate its average velocity.

Similarly, the change in momentum of an object can be calculated by knowing its initial and final velocities and the time taken for the velocity change to occur. This is essential in understanding the dynamics of collisions and other interactions between objects.